
- •Виды анализа и расчета электронных схем
- •Модели элементов и схем
- •Классификация моделей
- •Базовый набор элементов моделей
- •Пассивные элементы R, L, C
- •Пассивные компоненты и их модели
- •Резистор
- •Электрические конденсаторы
- •Реальная индуктивность
- •Трансформатор
- •Модели полупроводниковых приборов
- •Модель полупроводникового диода
- •Модель биполярного транзистора
- •Модель полевого транзистора
- •Макромодель операционного усилителя
- •Часть 2
- •Матрично-векторные параметры схем
- •Метод контурных токов
- •Метод узловых потенциалов
- •Функции электронных схем
- •Метод обобщенных ветвей
- •Введение, задачи анализа переходных процессов
- •Законы коммутации
- •Общая проблема и подход к анализу коммутационных процессов
- •Анализ переходных процессов в линейных цепях
- •Классический метод анализа переходных процессов
- •Операторный метод анализа переходных процессов
- •Временные методы анализа переходных процессов
- •Интеграл наложения
- •Интеграл Дюамеля
- •Частотный метод анализа переходных процессов
- •Дискретное преобразование Фурье
- •Интеграл Фурье
- •Анализ переходных процессов в нелинейных схемах.
- •СОДЕРЖАНИЕ
|
|
61 |
|
|
|
|
A |
2 |
∞ |
A2 |
|
P = |
0 |
|
+ ∑ |
k |
|
2 |
2 |
||||
|
|
k =1 |
Таким образом каждая гармоника выделяет в активном сопротивлении энергию, пропорциональную квадрату её амплитуды. Данное соотношение носит название равенства Парсеваля.
Так как энергия сигнала конечна, то несложно показать, что независимо от формы сигнала, если ряд Фурье существует, то амплитуда гармоники падает с ростом номера гармоники.
|
|
|
|
|
Дискретное преобразование Фурье |
|
|
|
|
|
|
|||||||||
|
В ряде современных задач электроники возникает необходимость восстановить функцию по её |
|||||||||||||||||||
дискретным отсчетам. Это диктуется прежде всего задачами цифровой обработки информации. Пред- |
||||||||||||||||||||
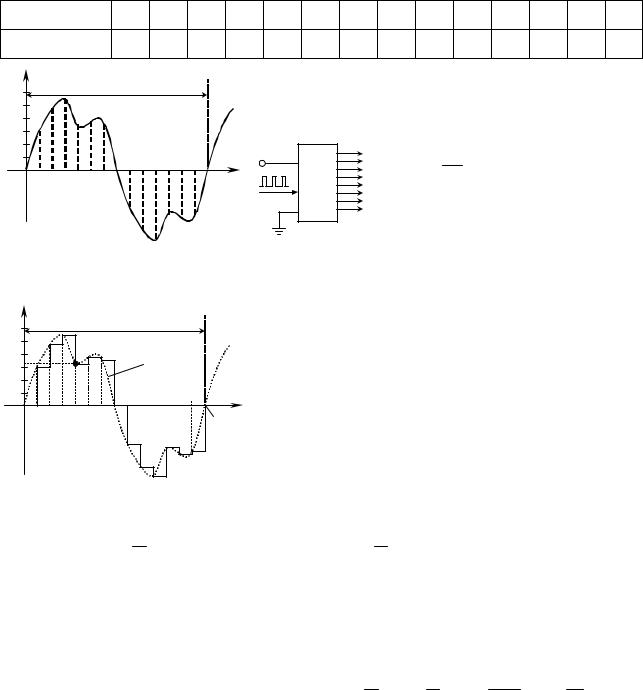
положим имеется непрерывная функция времени f1(t), которую с помощью технических устройств мож- |
||||||||||||||||||||
но измерять лишь в дискретные моменты времени. Это обеспечивается измерительным устройством |
||||||||||||||||||||
типа АЦП (рис. 3.20). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Таким образом на выходе системы мы имеем таблицу отсчетов: |
|
|
|
|
|
|
|||||||||||||
|
i |
0 |
|
1 |
2 |
|
3 |
4 |
5 |
6 |
|
|
7 |
8 |
9 |
|
10 |
11 |
12 |
13 |
|
F(ti) |
0 |
|
3 |
5 |
|
6 |
3 |
4 |
3 |
|
|
0 |
-3 |
-5 |
|
-6 |
-3 |
-4 |
-3 |
|
f(t) |
T |
|
|
|
|
|
|
|
|
|
|
|
Необходимо |
найти коэффициенты |
|||||
|
|
|
|
|
|
|
|
|
|
|
разложения в ряд Фурье непрерывной |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
функции f(t), заданной серией дискрет- |
||||||||
|
|
|
|
|
|
|
f(t) |
|
|
|
ных отсчетов на протяжении её периода. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
f (t) = A0 |
|
∞ |
|
cos(kω1t +ϕk ) |
|||||
0 |
|
|
|
|
|
t |
|
|
АЦП |
|
|
|
+∑Ak |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
k =1 |
|
|
|
|
||
|
|
|
|
|
|
|
Запуск |
|
|
|
|
|
Разложение в ряд Фурье необходи- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
мо для использования заново получен- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ной непрерывной функции в дальнейшей |
||||||||
|
|
|
Рис. 3.20. |
|
|
|
|
|
|
обработке (например для вывода ее на |
||||||||||
печатающее устройство, цифровой фильтрации, фильтрации высокочастотных шумов и других преоб- |
||||||||||||||||||||
разований, осуществляемых в частотной области). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
f(t) |
T |
|
|
|
|
|
Сразу же необходимо отметить, что при этом неизбежно |
||||||||||||
|
|
|
|
|
|
происходит потеря информации о поведении функции между |
||||||||||||||
f(ti) |
|
|
f(t) |
|
|
отсчетами! Поэтому разложение можно использовать лишь в |
||||||||||||||
|
|
|
|
случаях, когда Вы уверены в том, что частота дискретизации |
||||||||||||||||
|
|
|
|
|
tN-1 |
t |
достаточна для улавливания всех скоростных процессов в |
|||||||||||||
0 |
ti |
|
|
|
изменении функции (см. Теорему Котельникова-Найквиста в |
|||||||||||||||
|
|
|
tN=T |
курсе ЭПУ). |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
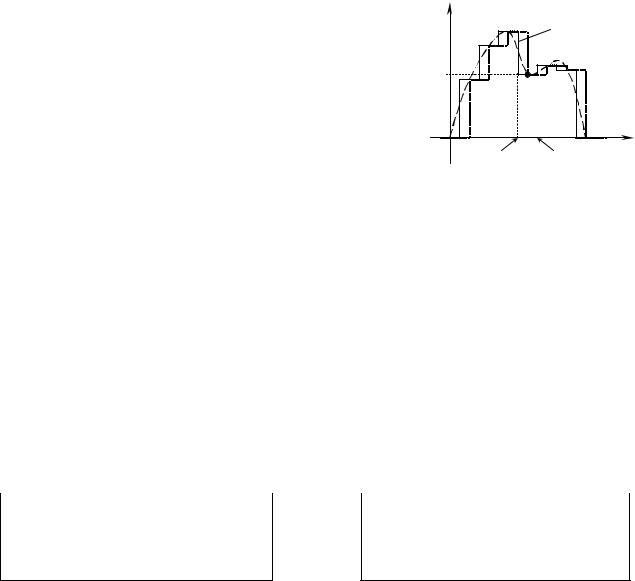
Простейшим подходом к разложению в этом случае яв- |
||||||||||||
|
|
|
|
|
|
|
ляется замена функции f(t) eё ступенчатой аппроксимацией |
|||||||||||||
|
|
Рис. 3.21. |
|
|
|
(см. рис. 3.21). |
|
|
|
|
|
|
|
|
|
|
|
|||
по формулам: |
|
|
|
|
Как известно, коэффициенты разложения определяются |
|||||||||||||||
|
T |
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
||
|
|
Bk = 2 |
f (x ) cos(kω1x )dx |
Ck |
= |
|
2 |
f (x ) sin(kω1x )dx . |
|
|
||||||||||
|
|
T |
∫0 |
|
|
|
|
|
|
|
T |
∫0 |
|
|
|
|
|
|
|
|
|
Будем вычислять функцию f(x), а также sin(kw1x) и cos(kw1x) в подынтегральном выражении, через |
|||||||||||||||||||
их дискретные отсчеты в моменты времени ti — f(ti) (т.е. используем ступенчатые аппроксимации для |
||||||||||||||||||||
обеих функций в подынтегральном выражении). Пусть на периоде Т имеется N+1 отсчетов непрерыв- |
||||||||||||||||||||
ной функции. Тогда ∆t=T/N; i=0...(N-1); |
t0=0; |
ti=∆t i. Тогда после несложных преобразований формулы |
||||||||||||||||||
для коэффициентов Bk, Ck приобретают вид: |
2πi |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
kω1xi |
= k 2π Ti |
= k |
2π |
i = |
k ; |
2 |
dx = 2 ∆x = |
|
2 |
∆t = |
2 |
|
|||||||
|
|
T |
|
N |
|
N |
|
N |
|
T |
|
|
T |
|
N∆t |
|
N |
|
||
62
|
2 |
N −1 |
2πi |
|
|
2 |
N −1 |
||
Bk = |
|
∑ f (ti ) cos |
|
k |
Сk = |
|
∑ |
||
N |
N |
N |
|||||||
|
i=0 |
|
|
|
i=0 |
||||
Естественно, что ступенчатая аппроксимация имеет большую погрешность, поэтому для коэффициентов ряда Фурье погрешность возрастает. Более точным является случай, когда на каждом интервале ∆t осуществляется аналитическое интегрирование функций cos(kw1x) и sin(kw1x), а ступенчатая аппроксимация функции сдвигается на полшага по оси времени (рис. 3.22), тем самым более точно аппроксимируя функцию. При этом коэффициенты разложения вычисляются следующим образом:
|
|
|
2 |
N −1 |
ti + |
∆t |
|
|
|
|
2 |
||||
Bk |
= |
∑ |
∫ f (ti ) cos(kω1x )dx = |
||||
T |
|||||||
|
|
i=0 |
ti − |
∆t |
|||
|
|
|
|
|
2 |
||
|
|
|
|
|
|
||
2πi |
|
|
||
f (ti ) sin |
N |
k |
|
|
|
|
|
||
f(t) |
|
|
сдвинутая |
|
|
|
|
||
|
|
|
аппрокс. |
|
f(ti) |
|
|
|
|
0 |
|
ti |
t |
|
ti-∆t/2 |
ti+∆t/2 |
|||
|
||||
|
Рис. 3.22. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ti + |
∆t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin(kω1x ) |
|
ti +∆t |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
N −1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
N −1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (ti ) |
|
|
|
2 = |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
|
∑ f (ti ) ∫cos(kω1x )dx |
= |
∑ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i=0 |
|
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
T |
i=0 |
|
|
|
|
|
|
|
|
kω |
|
|
|
|
∆t |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ti − |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
ti − |
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
ti + |
∆t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
N −1 |
|
|
|
|
|
|
|
|
sin k |
|
|
|
ω1 |
|
|
|
|
|
|
1 |
|
N −1 |
|
|
|
|
2πki |
|
|
πk |
|
|
2πki |
|
πk |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
= |
|
|
∑ |
f (ti ) |
|
|
tN |
|
|
|
|
|
|
|
|
= |
|
|
∑ f (ti |
) sin |
|
|
|
|
|
+ |
|
|
−sin |
|
|
− |
|
= |
|||||||||||||||||||||||
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
kπ |
|
N |
|
N |
|
N |
||||||||||||||||||||||||||||||||||||
|
|
N∆t i=0 |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆tN |
|
|
|
|
|
|
ti − |
∆t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 sin |
πk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
1 |
|
|
|
N −1 |
|
|
|
|
|
2πki |
|
|
πk |
|
|
|
|
N −1 |
|
|
|
|
|
|
|
2πki |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
= |
|
|
|
∑ f (ti ) 2 cos |
|
|
|
sin |
|
|
|
= |
|
|
|
N |
|
|
∑ f (ti ) cos |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
kπ |
|
N |
|
|
|
|
πk |
|
|
|
|
N |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2 |
|
sin |
πk |
|
|
|
N −1 |
|
|
|
|
|
2πi |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
sin |
πk |
N −1 |
|
|
|
2πi |
|
|
||||||||||||||||
|
Bk = |
|
|
|
|
|
N |
|
∑ f (ti ) cos |
|
|
|
|
k |
|
, аналогично |
Ck = |
|
|
|
|
|
|
|
|
N |
∑ f (ti ) sin |
|
k |
|
|||||||||||||||||||||||||||
N |
|
|
|
|
N |
|
|
N |
|
|
|
|
|
|
N |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
πk |
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
πk |
|
i=0 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для дальнейшего увеличения точности можно заменить f(t) не ступенькой, а кусочно-линейной аппроксимацией.
Таким образом для ДПФ необходимо выполнить пропорциональное N2 операций умножения. Если число отсчетов, и, следовательно, гармоник увеличивается, увеличивается пропорционально N2 и число операций умножения. Например, если N1=8, N2=32, то время расчета возрастает в 16 раз!
Для устранения этого недостатка существует группа методов, получивших название быстрого преобразования Фурье (БПФ).
Интеграл Фурье
Как известно разложение периодической функции, удовлетворяющей условиям Дирихле, в ряд Фурье имеет вид:
|
|
|
|
|
|
|
|
A0 |
|
|
|
|
∞ |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
f (t) = |
+ ∑[Bk cos(kω1t )+Ck sin(kω1t )] |
|
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|||
где k ω1 = ωk = k 2π/T принимает дискретные значения ω1=2π/T; ω2=2 2π/T... |
и т.д., а коэффициенты |
|||||||||||||||||||||
ряда вычисляются по формулам: |
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|||||||
|
|
|
+ |
T |
|
|
|
|
|
|
+ |
|
|
|
|
+ |
T |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
T |
2 |
|
|
T |
|
2 |
|
T |
|
2 |
|
|||||||||||
∫ |
|
|
|
∫ |
|
|
∫ |
|
||||||||||||||
A0 = |
2 |
|
|
|
|
f (x )dx ; |
Bk = |
2 |
|
|
|
|
|
f (x ) cos(kω1x )dx ; |
Ck = |
2 |
|
|
|
|
f (x ) sin(kω1x )dx |
|
|
− |
T |
|
|
|
− |
T |
|
− |
T |
||||||||||||
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
||||||
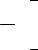
63
Интервал между круговыми частотами соседних гармоник:
∆ω =ωk +1 |
−ωk = [k +1 − k ] |
2π |
; |
|
2 |
= |
∆ω |
|
T |
T |
π |
||||||
|
|
|
|
|||||
Подставляя в формулу ряда Фурье значения коэффициентов A0, Bk, Ck:
|
|
+ |
T |
||
|
|
||||
∞ |
2 |
2 |
|||
+ ∑= |
|
|
∫ |
||
T |
|||||
k 1 |
|
− |
T |
||
|
|
|
|||
|
|
2 |
|||
Т.к. t не зависит от
+T
f (t) = 1 ∫2 f (x )dx + T −T2
|
|
|
+ |
T |
|
|
|
||
|
|
|
|||||||
f (x ) cos(kω1x )dx |
cos(kω1t )+ |
2 |
|
∫2 |
|
f (x ) sin(kω1x )dx sin(kω1t ) |
|||
|
|||||||||
|
T |
|
− |
T |
|
|
|
||
|
|
||||||||
|
|
|
2 |
|
|
|
|||
x, то его можно внести под знак интеграла:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
T |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (t) |
= |
1 |
|
∫2 f (x )dx + |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
− |
T |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
+ |
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
T |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||
|
∞ |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||
+ ∑= |
|
|
∫ |
f (x ) cos(kω1x ) cos(kω1t )dx + |
|
∫ f (x ) sin(kω1x ) sin(kω1t )dx |
= |
|||||||||||||||||||||||||||||||||||||
T |
T |
|||||||||||||||||||||||||||||||||||||||||||
|
k 1 |
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|||||||||||||
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||
|
|
+ |
T |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
2 |
|
|
|
|
|
|
|
∞ |
∆ω |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= |
∫ f (x )dx + ∑= |
|
|
∫ f (x ) [cos(kω1x ) cos(kω1t )dx +sin(kω1x ) sin(kω1t )] dx = |
||||||||||||||||||||||||||||||||||||||||
T |
π |
|||||||||||||||||||||||||||||||||||||||||||
|
|
− |
T |
|
|
|
|
|
|
k 1 |
|
|
|
|
|
− |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
T |
|
|
|
|
|
|
|
|
|
+ |
T |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
∞ |
|
∆ω |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
∫ f (x )dx + ∑= |
∫ f (x ) cos(kω1 |
(t − x )) dx |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
T |
π |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
T |
|
|
|
|
k |
1 |
|
|
|
− |
T |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Устремляя T к бесконечности, заключаем, что если функция f(x) абсолютно интегрируема в беско-
нечных пределах (т.е. если конечен интеграл |
+∞∫ |
|
|
f (x ) |
|
dx , то конечное значение имеет также инте- |
|||
|
|
||||||||
|
|
−∞ |
|
|
|
|
|
||
грал +∞∫ f (x ) cos(kω1 (t − x ))dx при любых ωk=k ω1 и t. При этом же условии: |
|||||||||
−∞ |
|
|
|
|
|
|
|
|
|
|
+ |
T |
|
|
|
|
|
||
1 |
2 |
|
|
|
|
|
|||
Tlim→∞ |
|
∫ |
|
|
f (x )dx = 0 |
||||
|
|
||||||||
T |
T |
|
|
|
|
|
|||
|
− |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||
При T→∞ ∆ω→0 (∆ω→dω), суммирование заменяется на интегрирование в пределах от 0 до
+∞. Таким образом, выражение для f(t) преобразуется к следующему виду: |
|
|||
f (t) = |
1 |
∞∫dω+∞∫ f (x ) cos(ω (t − x ))dx |
(1) |
|
π |
||||
0 |
−∞ |
|
||
Т.к. T→∞, функция f(t), заданная на промежутке -∞ ≤ t ≤ +∞ является уже непериодической функцией. Поэтому можно утверждать, что формула (1) представляет собой сумму бесконечно большого числа гармонических функций с непрерывно изменяющимися частотами ω и бесконечно малыми амплитудами. Таким образом, непериодическая функция характеризуется непрерывным спектром частот, в то время как периодическая функция — дискретным. Выражение (1) носит название интеграла Фу-
рье в тригонометрической форме.
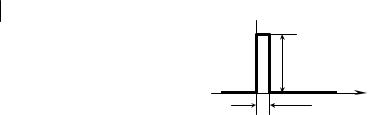
64
В силу четности функции cos(ω(t-x)) относительно ω можно записать:
|
|
|
1 |
+∞ |
+∞ |
|
|
f (t) = |
∫dω ∫ f (x ) cos(ω (t − x ))dx |
(2) |
|||||
2π |
|||||||
|
|
|
−∞ |
−∞ |
|
||
Рассмотрим теперь функцию |
1 |
+∞∫dω+∞∫ f (x ) sin(ω (t − x ))dx = 0. |
(3) |
||||
2π |
|||||||
|
|
−∞ |
−∞ |
|
|
||
Т.к. функция sin(ω (t-x)) нечетна относительно ω, то данный интеграл равен 0. Умножим теперь равенство (3) на j и сложим его с (2). Учтем при этом, что
e jωt = cos(ωt )+ j sin(ωt )
После данных несложных преобразований получаем интеграл Фурье в комплексной форме (4):
|
1 |
+∞ |
+∞ |
1 |
+∞ |
+∞ |
|
|
f (t) = |
∫dω ∫ f (x ) e jω (t−x )dx = |
∫e jωt dω ∫ f (x ) e−jωx dx |
(4) |
|||||
2π |
2π |
|||||||
|
−∞ |
−∞ |
−∞ |
−∞ |
|
|||
Если теперь рассмотреть внутренний интеграл как функцию от ω – F(jω)
F (jω)= +∞∫ f (τ) e− jωτ dτ , |
(5) |
|||
то |
−∞ |
|
|
|
|
+∞∫F( jω) e jωt dω |
|
||
f (t) = |
1 |
(6) |
||
2π |
||||
|
−∞ |
|
||
Если f(t) задана на промежутке от 0 до +∞, а на промежутке от -∞ до 0 равна нулю, то можно запи-
сать |
|
F (jω)= +∞∫ f (τ) e− jωτ dτ = F(ω) e jΘ(ω) |
(7) |
0 |
|
Равенство (7) — это одностороннее прямое преобразование Фурье. Комплексная функция час-
тоты F(jω) дает закон изменения комплексной амплитуды гармоник в зависимости от частоты ω и называется спектральной плотностью (спектральной или амплитудно-фазовой характеристикой, годографом) или, короче, спектром заданной функции f(t). F(ω) - амплитудно-частотная характеристика (четная функция частоты); Θ(ω) - фазочастотная характеристика (нечетная функция частоты). F(ω) также называют спектральной плотностью амплитуд или спектральной характеристикой непериодического сигнала; Θ(ω) — спектром фаз или фазовой характеристикой непериодического сигнала.
Равенство (6) представляет собой обратное преобразование Фурье.
Таким образом F(jω) по модулю и фазе характеризует гармонику частоты ω, а выражение (1/2π) F(jω) exp(jωt) представляет собой гармонику с частотой ω функции f(t). Эта гармоника выражена в комплексной форме, имеет бесконечно малую амплитуду и называется элементарной.
Сравнивая формулы прямого и обратного преобразования Лапласа
∞ |
|
1 |
|
σ + j∞ |
|
F( p) = L[f (t)]= ∫ f (t) e−pt dt |
f (t) = L−1[F( p)]= |
|
0 |
∫F ( p) ept dp |
|
2πj |
|
||||
0 |
|
|
σ0 |
− j∞ |
|
|
|
|
|||
с формулами прямого и обратного преобразования Фурье, заключаем, что преобразование Фурье является частным случаем преобразования Лапласа, получается из него при p = jω и применимо для более узкого класса функций f(t). Следовательно частотный спектр F(jω) функции f(t) получается из её Лапласова изображения F(p) по формуле:
F ( jω) = F( p) p=jω
Таким образом, имеется аналогия в преобразованиях Лапласа и Фурье, в частности и то, и другое можно использовать при расчете переходных процессов.
Рассмотрим спектр некоторых наиболее часто встречающихся сигналов. Для иллюстрации найдем спектр видеоимпульса - одиночного прямоугольного импульса, имеющего длительность tи (рис. 3.23).
 f(t)
f(t)
A
0 |
t |
tи
Рис. 3.23.
