
- •Кафедра высшей математики
- •Оглавление
- •Введение
- •Методические указания по теме «Интегральное исчисление функции одной переменной»
- •Справочный материал к контрольной работе по теме «Интегральное исчисление функции одной переменной»
- •2. Свойства неопределенного интеграла. Интегрирование методом подведения под знак дифференциала части подинтегральной функции
- •3. Интегрирование по частям
- •4. Интегрирование рациональных дробей
- •5. Интегрирование некоторых тригонометрических функций
- •6. Вычисление определенного интеграла по формуле Ньютона–Лейбница
- •7. Несобственные интегралы первого и второго рода
- •10. Вычисление объема тела вращения
- •11. Вычисление длины дуги плоской кривой
- •Примерный вариант и образец выполнения контрольной работы по теме «Интегральное исчисление функции одной переменной»
- •Варианты контрольной работы №5 по теме «Интегральное исчисление функции одной переменной»
- •Рекомендуемая литература
3. Интегрирование по частям
Формулой интегрирования по частям называют следующую формулу:
![]() .
(4)
.
(4)
Обычно
за
![]() выбирают
такое выражение, интегрирование которого
не вызывало бы трудностей, а за u
– функцию, дифференцирование которой
приводит к ее упрощению.
выбирают
такое выражение, интегрирование которого
не вызывало бы трудностей, а за u
– функцию, дифференцирование которой
приводит к ее упрощению.
Можно выделить два основных класса интегралов, берущихся по частям:
1)
![]() ;
;![]() ;
;![]() ;
;![]()
– здесь
за u
принимают
многочлен ![]() ,за
,за
![]() – оставшееся
выражение,тоесть, например
– оставшееся
выражение,тоесть, например
![]() .
.
2)
![]() ;
;![]() ;
;![]()
– здесь
за u
принимают обратную функцию, например,
arcsinbx,за
![]() – оставшееся
выражение,тоесть
– оставшееся
выражение,тоесть ![]() .
.
4. Интегрирование рациональных дробей
Рациональной
дробью
![]() называют отношение двух многочленов
называют отношение двух многочленов![]() и
и
![]() ,
т.е.
,
т.е.
![]() =
=![]() .
Для интегрирования
рациональной дроби необходимо
предварительно разложить
.
Для интегрирования
рациональной дроби необходимо
предварительно разложить
![]() ,
т.е. представить ее в виде суммы
элементарных дробей видов:
,
т.е. представить ее в виде суммы
элементарных дробей видов:
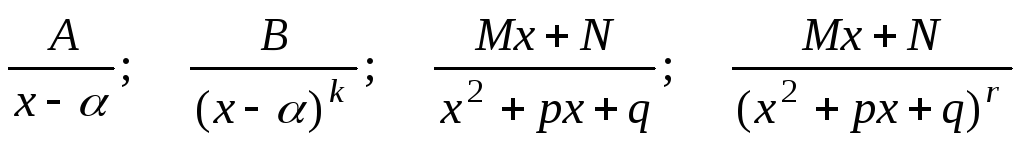 ,
,
где
k,
r
– целые положительные числа, а трехчлен
![]() не имеет действительных корней. Если
дробь
не имеет действительных корней. Если
дробь![]() неправильная (
неправильная (![]() ),
то необходимо предварительно выделить
целую часть дроби.
),
то необходимо предварительно выделить
целую часть дроби.
5. Интегрирование некоторых тригонометрических функций
Для
нахождения интегралов видов
![]() и
и![]() используют тригонометрические формулы:
используют тригонометрические формулы:
![]()
![]() (5)
(5)
Для
нахождения интегралов вида
![]() ,
гдеR
– рациональная функция (не содержащая
sinх
и cosx
под знаком корней), используют универсальную
подстановку:
,
гдеR
– рациональная функция (не содержащая
sinх
и cosx
под знаком корней), используют универсальную
подстановку:
![]() ,
которая сводит
,
которая сводит
![]() к интегралу от рациональной функции,
т.к.
к интегралу от рациональной функции,
т.к.
![]() и
и
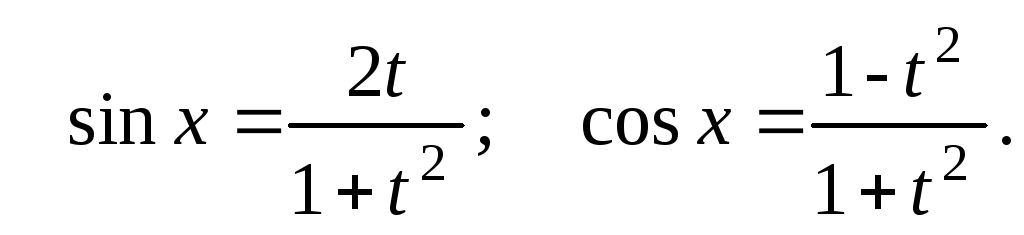 (6)
(6)
6. Вычисление определенного интеграла по формуле Ньютона–Лейбница
Формула Ньютона–Лейбница для вычисления определенного интеграла имеет вид:
![]() ,
(7)
,
(7)
если
![]() и
и![]() непрерывна на
непрерывна на![]() .
.
Пример
4. Вычислить
определенный интеграл![]() .
.
Решение. Это определенный интеграл, берущийся по частям, поэтому, применяя формулу (4), а затем формулу Ньютона–Лейбница, получаем:
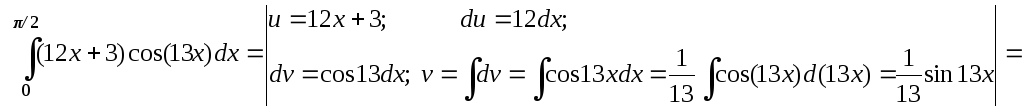
![]()
![]()
![]()
=![]() .
.
Ответ:
![]() .
.
7. Несобственные интегралы первого и второго рода
Интеграл
![]() (8)
(8)
называется несобственным интегралом первого рода.
Интеграл
![]() ,
(9)
,
(9)
где
a
– точка
бесконечного разрыва функции
![]() называетсянесобственным
интегралом второго рода.
называетсянесобственным
интегралом второго рода.
Если
b
– точка
бесконечного разрыва функции
![]() ,
то
,
то
![]() ,
(10)
,
(10)
– тоже несобственный интеграл второго рода.
Несобственный интеграл называется сходящимся, если существует конечный предел в правой части равенства. Если же предел не существует или равен бесконечности, то интеграл называется расходящимся.
Пример
5. Исследовать
на сходимость интеграл
![]() .
.
Решение. Это несобственный интеграл первого рода, поэтому
![]()
![]()
Следовательно,
интеграл сходится и равен
![]() .
.
Ответ:
интеграл сходится и равен
![]() .
.
Пример
6. Исследовать
на сходимость интеграл
![]() .
.
Решение. Это несобственный интеграл второго рода, так как х = 1 – точка разрыва второго рода подинтегральной функции, поэтому
![]()
![]() ,
,
следовательно, интеграл расходится.
Ответ: интеграл расходится.
8. Вычисление площади в декартовой системе координат (ДСК)
К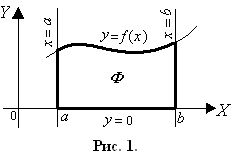 риволинейной
трапецией
в ДСК называется фигура, ограниченная
прямыми x
= a,
x=
b,
y
= 0 и кривой y
= f(x),
где
риволинейной
трапецией
в ДСК называется фигура, ограниченная
прямыми x
= a,
x=
b,
y
= 0 и кривой y
= f(x),
где
![]() для
для![]() (рис. 1).
(рис. 1).
Формула для вычисления площади криволинейной трапеции:
![]() .
(11)
.
(11)
Е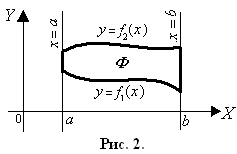 сли
фигураФ
ограничена в ДСК линиями x
= a,
x=
b,
y
= f1(x)
и
сли
фигураФ
ограничена в ДСК линиями x
= a,
x=
b,
y
= f1(x)
и
y
= f2(x)
где
![]() для
для![]() (рис. 2), то площадьФ
можно вычислить по формуле:
(рис. 2), то площадьФ
можно вычислить по формуле:
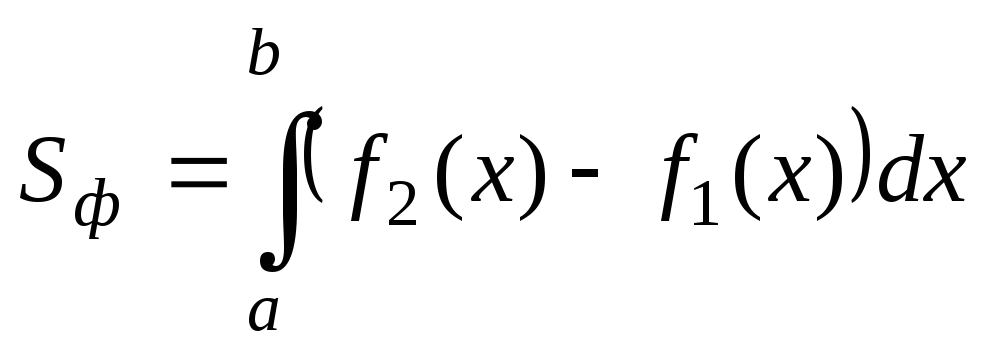 .
(12)
.
(12)
9. Вычисление площади в полярной системе координат (ПСК)
К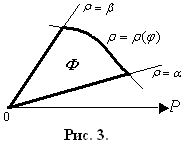 риволинейным
сектором в
ПСК называется фигура, ограниченная
лучами
риволинейным
сектором в
ПСК называется фигура, ограниченная
лучами
![]() и кривой
и кривой![]() ,
где
,
где![]() (рис. 3).
(рис. 3).
Формула для вычисления площади криволинейного сектора:
![]() .
(13)
.
(13)
