Числовые характеристики

Понятие математического ожидания М (Х) и дисперсии D(X) введенные ранее дискретной случайной величины, можно распространить на непрерывные случайные величины.

• Математическое ожидание М (Х) непрерывной случайной величины Х определяются равенством:

_+∞

M(X)= ∫ x•f(x)dx,

^-∞

при условии, что этот интеграл сходится абсолютно.

• Дисперсия D(X) непрерывной случайной величины Х определяется равенством:

_+∞

D(X)= ∫ (х-М(х)²)•f(x)dx, или

^-∞

_+∞

D(X)= ∫ х²•f(x)dx- (М(х))²

^-∞

• Среднее квадратическое отклонение σ(Х) непрерывной случайной величины определяется равенством:

Все свойства математического ожидания и дисперсии, рассмотренные ранее для дисперсных случайных величин, справедливы и для непрерывных.

Задача №3. Случайная величина Х задана дифференциальной функцией f(x):

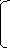0 при х≤0,

f(х)= х/3 при 0<х≤2,

1/3 при 2<х≤3,

0 при х>3.

Найти M(X),D(X),σ(Х), а также P(1<х<5)

Решение

_{+∞ 0 2 2 +∞ 2 3}

M(X)= ∫ х•f(x)dx=∫ х•0dx+∫ х•х/3 dx+∫ х/3dx+∫ 0•х•dx=1/3∫х²dx+1/3∫ хdx=

^-∞ _{0 3} ² ₃ ^{0 3 3 0 2}

= x³/9 + х²/6 = 8/9-0+9/6-4/6=31/18,

^{2 2}

_{+∞ 2 3 2 3}

D(X)= ∫ х²• f(x)dx-(М(х))²=∫ х²•х/3•dx+∫1/3х² dx=(31/18)²=х⁴/12 +х³/9 -

^{-∞ 0 2 0 2}

- (31/18)²=16/12-0+27/9-8/9-(31/18)²=31/9- (31/18)²==31/9(1-31/36)=155/324,

_{5 2 3 5 2 3}

P(1<х<5)= ∫ f(x)dx=∫ х/3 dx+∫ 1/3 dx+∫ 0 dx= х²/6 +1/3х =

^{1 1 2 3 1 2}

= 4/6-1/6+1-2/3=5/6.

Задачи для самостоятельного решения.

2.1.Непрерывная случайная величина Х задана функцией распределения:

0 при х≤0,

F(х)= при 0<х≤1,

1 при х>1.

Найти дифференциальную функцию распределения f (x), а также

Р(-1/2<Х<1/2).

2.2.Непрерывная случайная величина Х задана функцией распределения:

0 при х≤ π/6,

F(х)= -cos 3x при π/6<х≤ π/3,

1 при х> π/3.

Найти дифференциальную функцию распределения f (x), а также

Р(2π /9<Х< π /2).

2.3. Непрерывная случайная величина Х задана плотностью распределения:

0 при х≤2,

f(х)= с•х при 2<х≤4,

0 при х>4.

Найти: а) число с; б) М(Х), D(X).

2.4. Непрерывная случайная величина Х задана плотностью распределения:

0 при х≤0,

f(х)= с•√х при 0<х≤1,

0 при х>1.

Найти: а) число с; б) М(Х), D(X).

2.5. Задана плотность распределения вероятностей непрерывной случайной величины Х:

f(х)= при х[3;5],

0 при х [3;5].

Найти: а) F(х) и построить ее график; б) M(X),D(X), σ(Х); в) вероятность того, что в четырех независимых испытаниях величина Х примет ровно 2 раза значение, принадлежащее интервалу (1;4).

2.6. Задана плотность распределения вероятностей непрерывной случайной величины Х:

f(х)= 2(х-2) при х[2;3],

0 при х [2;3].

Найти: а) F(х) и построить ее график; б) M(X),D(X), σ (Х); в) вероятность того, что в трех независимых испытаниях величина Х примет ровно 2 раза значение, принадлежащее отрезку [1;2,5].

2.7. Функция f(х) задана в виде:

f(х)= при х[-√3/2 ; √3/2],

0 при х[-√3/2 ; √3/2].

Найти: а) значение постоянной с, при которой функция будет плотностью вероятности некоторой случайной величины Х; б) функцию распределения F(x).

2.8.Функция f(x) задана в виде:

f(х)= при х[- π /4 ; π /4],

0 при х[- π /4 ; π /4].

Найти: а) значение постоянной с, при которой функция будет плотностью вероятности некоторой случайной величины Х; б) функцию распределения F(x).

2.9. Случайная величина Х, сосредоточенная на интервале (3;7), задана функцией распределения F(х)= .Найти вероятность того, что

случайная величина Х примет значение: а) меньше 5, б) не меньше 7.

2.10. Случайная величина Х, сосредоточенная на интервале (-1;4),

задана функцией распределения F(х)= . Найти вероятность того, что

случайная величина Х примет значение: а) меньше 2, б) не меньше 4.

2.11. Случайная величина задана дифференциальной функцией распределения:

f(х)= при х[1; е],

0 при х[1; е].

Найти: а) число с; б) М(Х); в) вероятность Р(Х> М(Х)).

2.12. Случайная величина задана дифференциальной функцией распределения:

f(х)= при х[0; π],

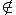0. при х[0; π].

Найти: а) М(Х); б) вероятность Р(Х≤М(Х))

2.13. Распределение Ремя задается плотностью вероятности:

0 при х<0,

f(х)= при х≥0.

Доказать, что f(x) действительно является плотностью распределения вероятностей.

2.14. Задана плотность распределения вероятностей непрерывной случайной величины Х:

0 при х<0,

f(х)= с•х•е^-х при х≥0.

Найти число с.

2.15.Случайная величина Х распределена по закону Симпсона (равнобедренного треугольника) на отрезке [-2; 2] (рис.4). Найти аналитическое выражение для плотности вероятности f(x) на всей числовой оси.

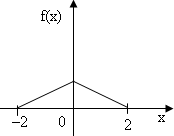(рис.4) 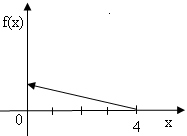(рис.5)

2.16. Случайная величина Х распределена по закону «прямоугольного треугольника» в интервале (0;4) (рис.5). Найти аналитическое выражение для плотности вероятности f(x) на всей числовой оси.

Ответы

2.1.

0 при х≤0,

f(х)= при 0<х≤1,

0. при х>1.

Р(-1/2<Х<1/2)= 2/3.

2.2. 0 при х≤ π/6,

F(х)= 3sin 3x при π/6<х≤ π/3,

0 при х> π/3.

Р(2π /9<Х< π /2)=1/2.

2.3. а) с=1/6, б) М(Х)=3 в) D(X)=26/81.

2.4. а) с=3/2, б) М(Х)=3/5 в) D(X)=12/175.

2.5. 0 при х≤3,

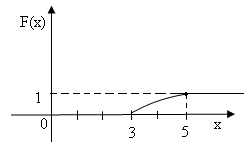
а) F(х)= 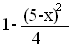при 3<х≤5,

1 при х>5.

б) M(X)=3 , D(X)=2/9, σ (Х)= √2/3;

в)3/8.

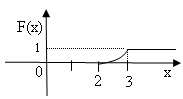
2.6. 0 при х≤2,

а) F(х)= (х-2)² при 2<х≤3,

1 при х>3.

б)M(X)=2 , D(X)=3, σ (Х)= ^≈ 1,893.

в)9/64.

2.7. а) с=

0 при х≤√3/2,

б) F(х)=

при -√3/2<х≤√3/2,

1 при х>√3/2.

2.8. а) с=1/2

0 при х≤- π /4,

б) F(х)= при - π /4 <х≤ π /4,

1 при х> π /4.

2.9. а)1/4; б) 0.

2.10. а)3/5; б) 1.

2.11.а)с=2; б)М(Х)=2; в)1-ln²2≈0,5185.

2.12. а) М(Х)= π /2 ; б) 1/2

2.14. с=1.

2.15.f(х)= при х[-2; 2],

0 при х[-2; 2].

2.16. f(х)= при х(0;4),

0 при х(0;4).