
АиГ / тема 7
.docКурс “Алгебра и Геометрия”
(спец. прикладная математика, информатика, 1 курс, 1 семестр)
Тема 7. Уравнения прямой на плоскости. – 2 ч.
Содержание: общее уравнение прямой, уравнение прямой с угловым коэффициентом; угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых; уравнение прямой, проходящей через две данные точки; неполные уравнения прямой; уравнение прямой в отрезках; нормальное уравнение, расстояние от точки до прямой; полярное уравнение прямой; уравнение пучка прямых.
Цель: изучить различные способы задания прямых на плоскости их уравнениями; научиться применять уравнения прямых при решении планиметрических задач.
Форма контроля: опрос.
Задачи
Задача
1 ([8], 216). Даны
уравнения двух сторон параллелограмма
![]() ,
,
![]() и уравнение одной из его диагоналей
и уравнение одной из его диагоналей
![]() .
Определить координаты вершин этого
параллелограмма.
.
Определить координаты вершин этого
параллелограмма.
Задача
2 ([8], 217).
Стороны треугольника лежат на прямых
![]() ,
,
![]() ,
,
![]() .
Вычислить его площадь
.
Вычислить его площадь
![]() .
.
Задача
3 ([8], 218).
Площадь треугольника
![]() кв. ед.; две его вершины - точки
кв. ед.; две его вершины - точки
![]() и
и
![]() ,
а третья вершина
,
а третья вершина
![]() лежит на прямой
лежит на прямой
![]() .
Определить координаты вершины
.
Определить координаты вершины
![]() .
.
Задача
4 ([8], 220).
Составить уравнение прямой и построить
прямую на чертеже, зная её угловой
коэффициент
![]() и отрезок
и отрезок
![]() ,
отсекаемый ею на оси Oy:
,
отсекаемый ею на оси Oy:
1)
![]() ,
,
![]() ;
2)
;
2)
![]() ,
,
![]() ;
3)
;
3)
![]() ,
,
![]() ;
4)
;
4)
![]() ,
,
![]() ;
;
5)
![]() ,
,
![]() ;
6)
;
6)
![]() ,
,
![]() .
.
Задача
5 ([8], 221).
Определить угловой коэффициент
![]() и отрезок
и отрезок
![]() ,
отсекаемый на оси Oy, для каждой из прямых:
,
отсекаемый на оси Oy, для каждой из прямых:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() .
.
Задача
6 ([8], 222). Дана
прямая
![]() .
Определить угловой коэффициент
.
Определить угловой коэффициент
![]() прямой:
прямой:
-
параллельной данной прямой;
-
перпендикулярной к данной прямой.
Задача
7 ([8], 223). Дана
прямая
![]() .
Составить уравнение прямой, проходящей
через точку
.
Составить уравнение прямой, проходящей
через точку
![]() :
:
-
параллельной данной прямой;
-
перпендикулярной к данной прямой.
Задача
8 ([8], 224). Даны
уравнения двух сторон прямоугольника
![]() ,
,
![]() и одна из его вершин
и одна из его вершин
![]() .
Составить уравнения двух других сторон
этого прямоугольника.
.
Составить уравнения двух других сторон
этого прямоугольника.
Задача
9 ([8], 225). Даны
уравнения двух сторон прямоугольника
![]() ,
,
![]() и уравнение одной из его диагоналей
и уравнение одной из его диагоналей
![]() .
Найти вершины прямоугольника.
.
Найти вершины прямоугольника.
Задача
10 ([8], 226).
Найти проекцию точки
![]() на прямую
на прямую
![]() .
.
Задача
11 ([8], 227).
Найти точку
![]() ,
симметричную точке
,
симметричную точке
![]() относительно прямой
относительно прямой
![]() .
.
Задача 12 ([8], 228). В каждом из следующих случаев составить уравнение прямой, параллельной двум данным прямым и проходящей посередине между ними:
1)
![]() ,
,
![]() ;
;
2)
![]() ,
,
![]() ;
;
3)
![]() ,
,
![]() ;
;
4)
![]() ,
,
![]() ;
;
5)
![]() ,
,
![]() .
.
Задача
13 ([8], 253).
Определить угол
![]() между двумя прямыми:
между двумя прямыми:
1)
![]() ,
,
![]() ;
;
2)
![]() ,
,
![]() ;
;
3)
![]() ,
,
![]() ;
;
4)
![]() ,
,
![]() .
.
Задача
14 ([8], 254). Дана
прямая
![]() .
Составить уравнение прямой, проходящей
через точку
.
Составить уравнение прямой, проходящей
через точку
![]() под углом 45o
к данной прямой.
под углом 45o
к данной прямой.
Задача
15 ([8], 272).
Составить уравнения сторон треугольника,
зная одну из его вершин
![]() и уравнения двух биссектрис
и уравнения двух биссектрис
![]() и
и
![]() .
.
Задача
16 ([8], 273).
Составить уравнения сторон треугольника,
зная одну его вершину
![]() ,
а так же уравнения высоты
,
а так же уравнения высоты
![]() и биссектрисы
и биссектрисы
![]() ,
проведённых из одной вершины.
,
проведённых из одной вершины.
Задача
17 ([8], 274).
Составить уравнения сторон треугольника,
зная одну его вершину
![]() ,
а так же уравнение высоты
,
а так же уравнение высоты
![]() и биссектрисы
и биссектрисы
![]() ,
проведённых из различных вершин.
,
проведённых из различных вершин.
Задача
18 ([8], 275).
Составить уравнения сторон треугольника,
зная одну его вершину
![]() ,
а так же уравнение высоты
,
а так же уравнение высоты
![]() и медианы
и медианы
![]() ,
проведённых из одной вершины.
,
проведённых из одной вершины.
Задача
19 ([8], 276). Составить
уравнения сторон треугольника, зная
одну его вершину
![]() ,
а так же уравнение высоты
,
а так же уравнение высоты
![]() и медианы
и медианы
![]() ,
проведённых из различных вершин.
,
проведённых из различных вершин.
Задача
20 ([8], 277).
Составить уравнения сторон треугольника,
зная одну его вершину
![]() ,
а так же уравнение биссектрисы
,
а так же уравнение биссектрисы
![]() и медианы
и медианы
![]() ,
проведённых из одной вершины.
,
проведённых из одной вершины.
Задача
21 ([8], 278).
Составить уравнения сторон треугольника,
зная одну его вершину
![]() ,
а так же уравнение биссектрисы
,
а так же уравнение биссектрисы
![]() и медианы
и медианы
![]() ,
проведённых из разных вершин.
,
проведённых из разных вершин.
Задача
22 ([8], 286).
Определить, при каких значениях
![]() и
и
![]() прямая
прямая
![]() параллельна оси абсцисс и отсекает на
оси ординат отрезок, равный -3 (считая
от начала координат). Написать уравнение
этой прямой.
параллельна оси абсцисс и отсекает на
оси ординат отрезок, равный -3 (считая
от начала координат). Написать уравнение
этой прямой.
Задача
23 ([8], 292).
Определить при каких значениях
![]() и
и
![]() две прямые
две прямые
![]() ,
,
![]() .
.
-
параллельны;
-
совпадают;
-
перпендикулярны.
Задача
24 ([8], 304).
Составить уравнение прямой, которая
проходит через точку
![]() и отсекает от ординарного угла треугольник
с площадью, равной
и отсекает от ординарного угла треугольник
с площадью, равной
![]() кв. ед.
кв. ед.
Задача
25 ([8], 307).
Через точку
![]() проведена прямая, отсекающая от
координатного угла треугольник, площадь
которого равна 3 кв. ед. Определить точки
пересечения этой прямой с осями координат.
проведена прямая, отсекающая от
координатного угла треугольник, площадь
которого равна 3 кв. ед. Определить точки
пересечения этой прямой с осями координат.
Задача
26 ([8], 312).
Вычислить величину отклонения
![]() и расстояние
и расстояние
![]() точки от прямой в каждом из следующих
случаев:
точки от прямой в каждом из следующих
случаев:
-
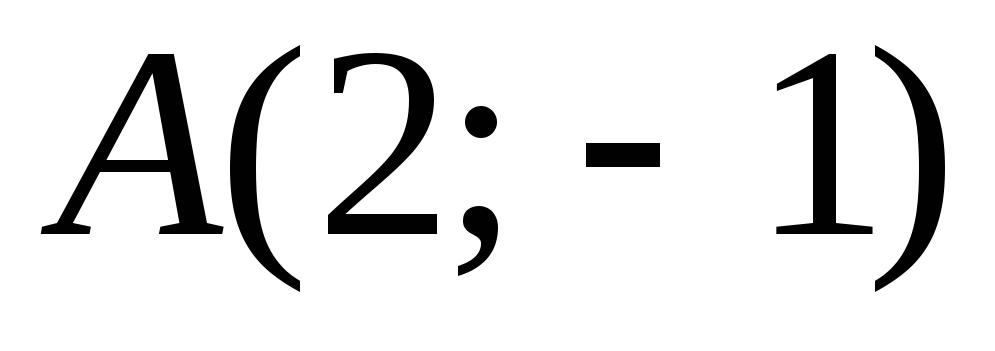 ,
,
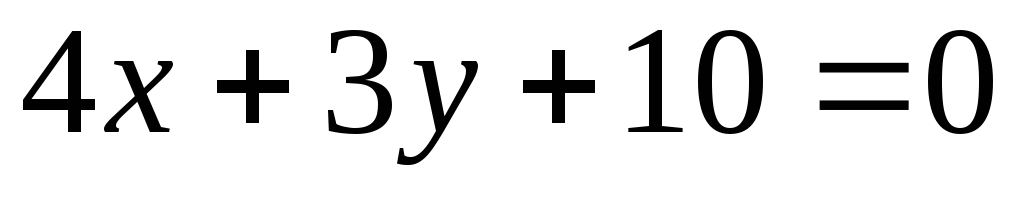 ;
2)
;
2)
 ,
,
 ;
;
3)
![]() ,
,
![]() ;
4)
;
4)
![]() ,
,
![]() .
.
Задача
27 ([8], 324).
Доказать, что прямая
![]() параллельна прямым
параллельна прямым
![]() ,
,
![]() и делит расстояние между ними пополам.
и делит расстояние между ними пополам.
Задача
28 ([8], 333).
Точка
![]() является вершиной квадрата, одна из
сторон которого лежит на прямой
является вершиной квадрата, одна из
сторон которого лежит на прямой
![]() .
Составить уравнения прямых, на которых
лежат остальные стороны этого квадрата.
.
Составить уравнения прямых, на которых
лежат остальные стороны этого квадрата.
Задача
29 ([8], 336).
Отклонения точки
![]() от прямых
от прямых
![]() и
и
![]() равны соответственно -3 и -5. Определить
координаты точки
равны соответственно -3 и -5. Определить
координаты точки
![]() .
.
Задача 30 ([8], 339). Составить уравнения биссектрис углов, образованных двумя пересекающимися прямыми:
1)
![]() ,
,
![]() ;
2)
;
2)
![]() ,
,
![]() ;
;
3)
![]() ,
,
![]() .
.
Задача
31 ([8], 349).
Составить уравнения биссектрисы угла
между прямыми
![]() и
и
![]() ,
в котором лежит точка
,
в котором лежит точка
![]() .
.
Задача
32 ([8], 353).
Найти центр пучка прямых, данного
уравнения
![]() .
.
Задача
33 ([8], 359). Даны
уравнения сторон треугольника
![]() ,
,
![]() ,
,
![]() .
Не определяя координат его вершин,
составить уравнения высот этого
треугольника.
.
Не определяя координат его вершин,
составить уравнения высот этого
треугольника.
Задача
34 ([8], 360).
Составить уравнение прямой, проходящей
через точку пересечения прямых
![]() ,
,
![]() под углом в 45о
к прямой
под углом в 45о
к прямой
![]() .
Решить задачу, не вычисляя координат
точки пересечения данных прямых.
.
Решить задачу, не вычисляя координат
точки пересечения данных прямых.
Задача
35 ([8], 363). Дано
уравнение пучка прямых
![]() .
Найти прямые этого пучка, отрезки
которых, заключённые между прямыми
.
Найти прямые этого пучка, отрезки
которых, заключённые между прямыми
![]() ,
,
![]() ,
равны
,
равны
![]() .
.
Задача
36 ([8], 364). Дано
уравнение пучка прямых
![]() .
Доказать, что прямая
.
Доказать, что прямая
![]() принадлежит этому пучку.
принадлежит этому пучку.
Задача 37 ([8], 381). Вывести полярное уравнение прямой, если даны:
-
угол
 наклона прямой к полярной оси и длина
перпендикуляра
наклона прямой к полярной оси и длина
перпендикуляра
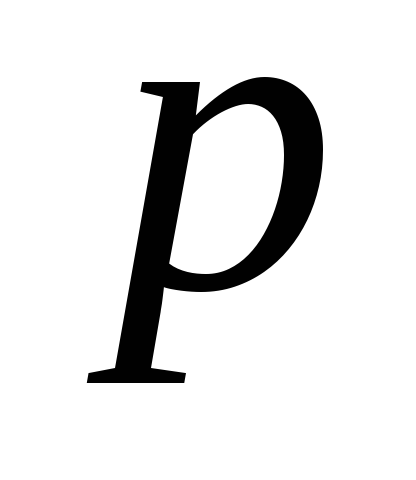 ,
опущенного из полюса на эту прямую.
Написать уравнение этой прямой в случае
,
опущенного из полюса на эту прямую.
Написать уравнение этой прямой в случае
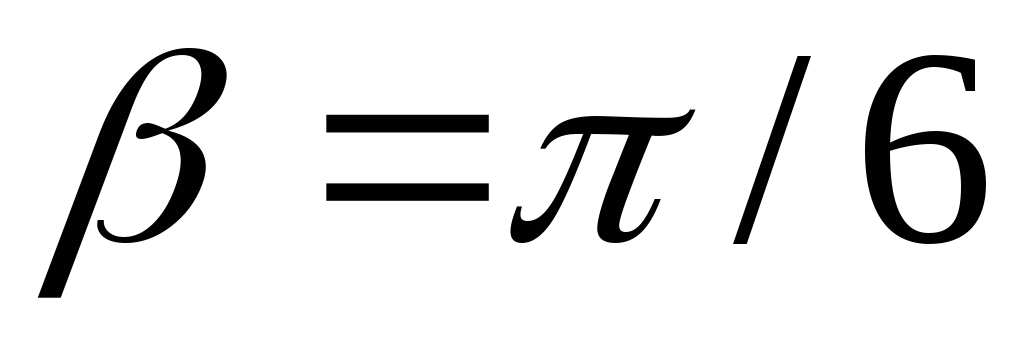 ,
,
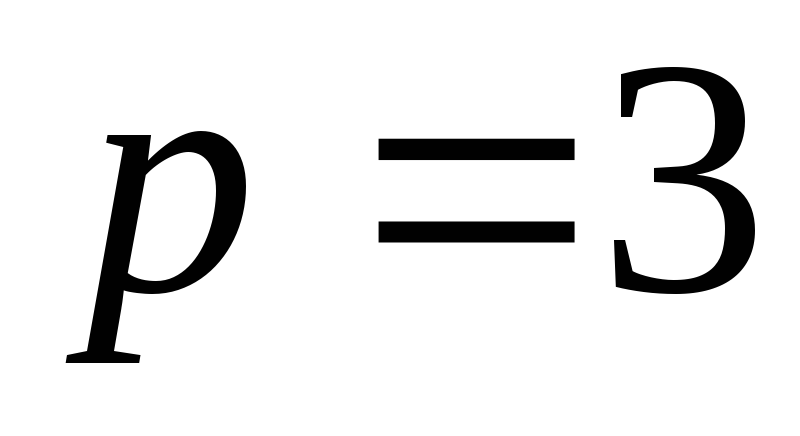 ;
; -
отрезок
 ,
который отсекает прямая на полярной
оси, считая от полюса, и полярный угол
,
который отсекает прямая на полярной
оси, считая от полюса, и полярный угол
 нормали этой прямой. Написать уравнение
этой прямой в случае
нормали этой прямой. Написать уравнение
этой прямой в случае
 ,
,
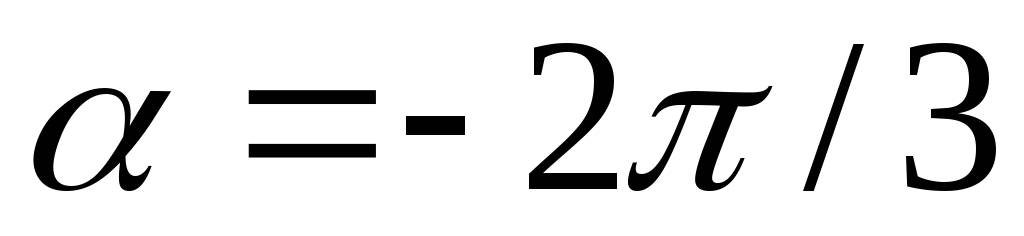 ;
; -
угол
 наклона этой прямой к полярной оси и
отрезок
наклона этой прямой к полярной оси и
отрезок
 ,
который отсекает прямая на полярной
оси, считая от полюса. Написать уравнение
этой прямой в случае
,
который отсекает прямая на полярной
оси, считая от полюса. Написать уравнение
этой прямой в случае
 ,
,
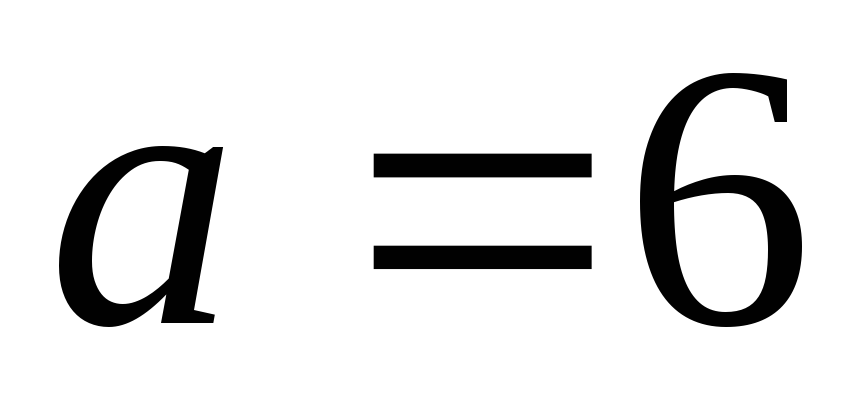 .
.
Задача
38 ([8], 384).
Составить уравнение прямой, проходящей
через точки
 и
и
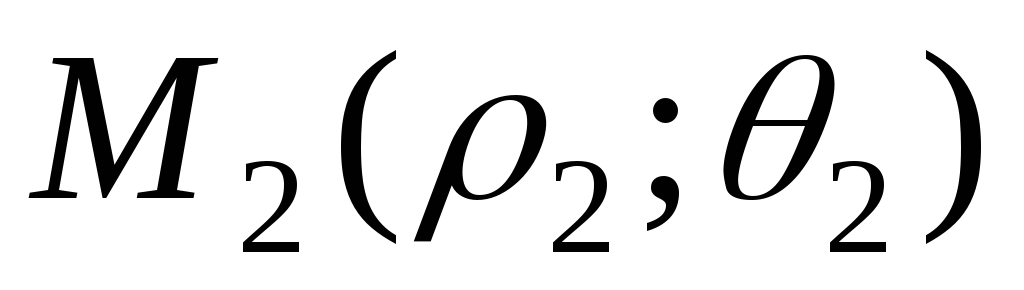 .
.
Тема 7. Различные виды уравнения прямой на плоскости.
Ответы
Задача
1.
![]() ,
,
![]() ,
,
![]() и
и
![]() .
.
Задача
2.
![]() кв. ед.
кв. ед.
Задача
3.
![]() или
или
![]() .
.
Задача
4.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() ;
5)
;
5)
![]() ;
6)
;
6)
![]() .
.
Задача
5. 1)
![]() ,
,
![]() ;
2)
;
2)
![]() ,
,
![]() ;
3)
;
3)
![]() ,
,
![]() ;
;
4)
![]() ,
,
![]() ;
5)
;
5)
![]() ;
;
![]() .
.
Задача
6.
1)
![]() ;
2)
;
2)
![]() .
.
Задача
7. 1)
![]() ;
2)
;
2)
![]() .
.
Задача
8.
![]() ,
,
![]() .
.
Задача
9.
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Задача
10.
![]() .
.
Задача
11.
![]() .
.
Задача
12.
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() .
.
Задача
13.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() — прямые параллельны; 4)
— прямые параллельны; 4)
![]() .
.
Задача
14.
![]() или
или
![]() .
.
Задача
15.
![]() ,
,
![]() ,
,
![]() .
Указание.
Если на одной стороне угла дана точка
.
Указание.
Если на одной стороне угла дана точка
![]() ,
то точка, симметричная точке
,
то точка, симметричная точке
![]() относительно биссектрисы этого угла,
будет лежать на другой его стороне.
относительно биссектрисы этого угла,
будет лежать на другой его стороне.
Задача
16.
![]() ,
,
![]() ,
,
![]() .
.
Задача
17.
![]() ,
,
![]() ,
,
![]() .
.
Задача
18.
![]() ,
,
![]() ,
,
![]() .
.
Задача
19.
![]() ,
,
![]() ,
,
![]() .
.
Задача
21.
![]() ,
,
![]() ,
,
![]() .
.
Задача
22.
![]() ,
,
![]() ,
,
![]() .
.
Задача
22.
![]() ,
,
![]() ,
,
![]() .
.
Задача
23.
1)
![]() ,
,
![]() или
или
![]() ,
,
![]() ;
2)
;
2)
![]() ,
,
![]() или
или
![]() ,
,
![]() ;
3)
;
3)
![]() ,
,
![]() – любое значение.
– любое значение.
Задача
24.
Условию задачи удовлетворяют следующие
три прямые:
![]() ,
,
![]() ,
,
![]() .
.
Задача
25.
Условию задачи удовлетворяют две прямые,
пересекающие соответственно оси
координат в точках
![]() ,
,
![]() и
и
![]() ,
,
![]() .
.
Задача
26.
1)
![]() ,
,
![]() ;
2)
;
2)
![]() ,
,
![]() ;
3)
;
3)
![]() ,
,
![]() ;
;
4)
![]() ,
,
![]() — точка
— точка
![]() лежит на прямой.
лежит на прямой.
Задача
28.
Условию задачи удовлетворяют два
квадрата; остальные стороны одного из
них лежат на прямых
![]() ,
,
![]() ,
,
![]() ;
остальные стороны другого — на прямых:
;
остальные стороны другого — на прямых:
![]() ,
,
![]() ,
,
![]() .
.
Задача
29.
![]() .
.
Задача
30.
1)
![]() ,
,
![]() ;
2)
;
2)
![]() ,
,
![]() ;
3)
;
3)
![]() ,
,
![]() .
.
Задача
31.
![]() .
.
Задача
32.
![]() .
.
Задача
33.
![]() ,
,
![]() ,
,
![]() .
.
Задача
34.
![]() ,
,
![]() .
.
Задача
35.
![]() ,
,
![]() .
.
Задача
36.
1)
![]()
2)
![]()
3)
![]()
Задача
38.
![]()
