2.3 Многообразия Грассмана

Описываемое ниже клеточное разбиение многообразий Грассмана очень важно для геометрии и топологии (особенно для теории характеристических классов). Составляющие его клетки называются клетками Шуберта, а само оно называется шубертовским.

Пусть - произвольная конечная (возможно, пустая) невозрастающая последовательность целых положительных чисел, не превосходящих, причем. Обозначим черезподмножество пространства, составленное из подпространствпространстваR, удовлетворяющих следующим условиям (мы полагаем):

Rпри;

codim(R)при;

Rпри

(мы считаем, что R^aRпри:). Приведем другое, более простое описание множества.Напомним, что диаграмма Юнга набора- это фигура, которая рисуется на клетчатой бумаге, как показано на рис.4а (столбцы имеют длины). Число клеток диаграммы Юнга равно. Можно считать, что клетки пространстваотвечают диаграммам Юнга, вмещающимся в прямоугольник(рис.4а). Рассмотрим диаграмму Юнга набораи расположим ее, как показано на рис.4б. Толстая линия на этом рисунке представляет собой график некоторой неубывающей функции, и множествозадается условием dim(R) =. Ввиду наличия такого простого описания, множествообозначают иногда через, где- обозначение для диаграммы Юнга набора. Еще раз заметим, что размерность клеткиравна числу клеток диаграммы.

Лемма. Множество гомеоморфноR.

Доказательство. Расчленим диаграмму Юнга набора , как показано на рис.4в. Поставим в клетках вдоль косых линий единицы, в заштрихованные клетки - произвольные числа и в остальные места - нули. Получится-матрица, строки которой составляют базис некоторого-мерного подпространства пространстваR. Легко понять, что это подпространство принадлежити что всякое подпространство, принадлежащее, обладает единственным базисом указанного вида. Получаем параметризацию клеткинаборами изчисел (числа в заштрихованных клетках).

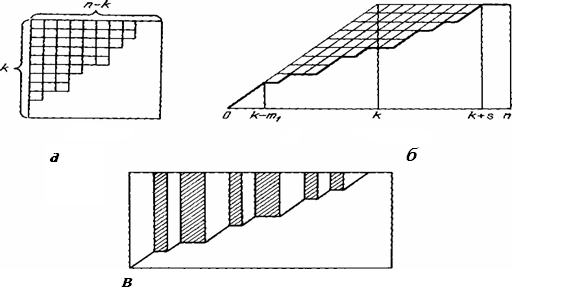
Рис.4

На самом деле верно больше: множества составляют клеточное разбиение пространства. Для доказательства нужно построить характеристические отображения, т.е. продолжить построенные гомеоморфизмыRдо непрерывных отображений, отображающих сферув объединение клеток меньших размерностей.

Замечательное свойство шубертовских клеток состоит в том, что при естественных вложениях ви вклеткагомеоморфно накладывается на клетку того же наименования. Следовательно, пространстворазбивается на клетки Шуберта, отвечающие диаграммам Юнга, содержащимся в горизонтальной полуполосе высоты, а пространстворазбивается на клетки, отвечающие всем без исключения диаграммам Юнга. Во всех случаях размерности клеток равны числам клеток диаграмм Юнга.

Комплексные и кватернионные аналоги шубертовских клеток очевидны; разумеется, размерности комплексных и кватернионных аналогов клеток Шуберта соответственно в 2 и 4 раза превосходят числа клеток соответствующих диаграмм Юнга.

2.4 Многообразия флагов

Многообразия флагов имеют естественное клеточное разбиение, обобщающее шубертовское разбиение многообразий Грассмана. Это разбиение и его клетки также называются шубертовскими. Опишем разбиение в вещественном случае (комплексный и кватернионный случаи отличаются только удвоением и учетверением размерностей клеток).

Шубертовские клетки многообразия флагов характеризуются наборами размерностей пересеченийR. Числа, однако, должны удовлетворять набору довольно неудобных условий, и мы предпочтем следующее, более рациональное описание клеток Шуберта.

Клетки пространства отвечают наборамцелых чисел, принимающих значения, причем ровноиз этих чисел равны(; мы считаем, чтои). Клетка, отвечающая набору ,состоит из флагов ,у которых

dim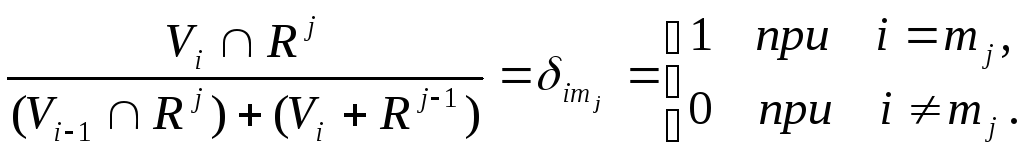

(мы считаем, что иесть все пространствоR) или, иначе,

dimcard.

Размерность клетки равна числу пар, для которых,>.

В частности, многообразие полных флагов разбито наклеток, отвечающих обыкновенным перестановкам чисел, причем размерность клетки равна числу инверсий в перестановке.

Если многообразие флагов есть многообразие Грассмана , тои набор состоит изединиц идвоек. Построим по этому набору-звенную ломаную на плоскости, начинающуюся в точкеи кончающуюся в точке. Все звенья ломаной имеют длину 1, причем-eзвено направлено вниз, если, и вправо, если. Эта ломаная ограничивает (вместе с координатными осями) некоторую диаграмму Юнга, и легко понять, что.

Заметим в заключение, что клетки (и их комплексные и кватернионные аналоги) могут быть описаны чисто групповым образом: это - орбиты группы нижних треугольных-матриц с единицами на диагонали, естественным образом действующей в многообразии флагов. Именно, клеткаесть орбита флага,-е пространство которого порождено координатными векторами, номеракоторых удовлетворяют неравенству.