8. Непрерывные отображения

Содержание: Определение непрерывного отображения. Простейшие свойства непрерывных отображений. Критерии непрерывности отображения. Некоторые конструкции, связанные с непрерывными отображениями топологических пространств. Открытые и замкнутые отображения. Гомеоморфизмы.

Необходимо научиться проверять непрерывность заданного отображения, знать и уметь применять свойства непрерывных отображений.

Основные определения

Пусть f – отображение пространства X в пространство Y.

Отображение f называется непрерывным в точке a пространства X, если для каждой окрестности V точки существует окрестностьU точки a, такая, что .

Отображение f непрерывно, если оно непрерывно в каждой точке пространства X.

Отображение f называют открытым, если при этом отображении образ каждого открытого в X множества открыт в Y. Отображение f называют замкнутым, если при этом отображении образ каждого замкнутого в X множества замкнут в Y.

Вопросы для повторения

1. Что следует понимать под топологическим свойством отображения топологических пространств?

2. Являются ли топологическими свойствами непрерывность, открытость, замкнутость отображений топологических пространств?

3. Сформулируйте известное из курса математического анализа определение Коши непрерывности отображения метрических пространств. Как это определение связано с данным выше определением непрерывности отображения топологических пространств?

Задания

1. Пусть f – отображение пространства X во множество Y, ,. Доказать, что– окрестность точкиq тогда и только тогда, когда в X существует содержащее точку q открытое множество W, для которого .

2. Доказать, что отображение топологических пространств непрерывно в точкепространстваX тогда и только тогда, когда для любого подмножества M пространства X из следует .

3. Пусть f – отображение метрического пространства в метрическое пространство,. Доказать:

1) f непрерывно в точке q тогда и только тогда, когда для любого положительного числа существует положительное числотакое, что для каждой точкииз неравенстваследует неравенство.

2) если для каждой точки выполняется неравенство , то f непрерывно в точке q.

4. Пусть f – отображение пространства X в пространство Y, и пространствоX имеет счетную базу в точке q. Доказать, что непрерывно в точкеq в том и только том случае, если для любой последовательности точек, принадлежащих пространствуX, из следует.

5. Пусть f – отображение пространства X в пространство Y, , Z – подпространство пространства Y, содержащее . Доказать, чтоf непрерывно в точке q в том и только том случае, если f, рассматриваемое как отображение X в Z , непрерывно в точке q.

6. Пусть X, Y, Z – топологические пространства, отображение непрерывно в точке q пространства X, а отображение непрерывно в точке . Доказать, что композиция непрерывна в точке q.

7. Пусть − отображение топологических пространств, , – предбаза в точке пространства Y. Доказать, что f непрерывно в точке q, если для каждого множествоявляется окрестностью точкиq.

8. Пусть − непрерывное отображение,− база пространстваX, – база пространстваY. Можно ли утверждать, что

а) − база в?

б) − база вX ?

9. Доказать, что отображение f пространства X в пространство непрерывно тогда и только тогда, когда для любого подмножествапространства X имеем: .

10. Пусть f – отображение пространства X в пространство Y, − открытое подпространство пространства X, и непрерывно в точке x. Доказать, что f непрерывно в точке x.

11. Пусть – отображение топологических пространств,,, и при этоминепрерывны. Доказать, чтоf непрерывно.

12. Пусть и− замкнутые подпространства пространства X, и . Доказать:

а) если , а отображения и непрерывны в точке q, то f непрерывно в точке q;

б) если и непрерывны, тоf непрерывно.

13. Пусть f и g – непрерывные отображения топологического пространства X в T₂-пространство Y. Доказать, что множество замкнуто.

14. Пусть f и g – непрерывные отображения пространства X в T₂-пространство Y, D – всюду плотное подмножества пространства X, и при этом . Доказать, чтоf = g.

15. Пусть ,,. Определим отображение

(называемое функцией Дирихле) пространства в дискретное двоеточие {0; 1}. Доказать, что это отображение не является непрерывной ни в одной точке пространстваX. В то же время, отображения инепрерывны.

16. Может ли отображение евклидовой плоскости в евклидову прямую быть непрерывным по каждой из двух «переменных», но не являться при этом непрерывным отображением?

17. Доказать, что для каждого всякое аффинное преобразование евклидова пространства является гомеоморфизмом.

18. Доказать, что для каждого всякое проективное преобразование проективного пространства с естественной топологией на нем является гомеоморфизмом.

19. Рассматривая каждое множество вещественных чисел как подпространство евклидовой прямой , доказать:

1. Если ,, то отображение– топологическое преобразование прямой;

2. Отображение – топологическое преобразование «проколотой прямой».

3. Отображение – гомеоморфизмна.

4. Отображение – гомеоморфизмна.

5. Отображение − гомеоморфизмна .

6. Отображение − гомеоморфизм на .

7. Два бесконечных промежутка евклидовой прямой гомеоморфны в следующих случаях:

а) каждый из двух промежутков либо является замкнутым и неограниченным, либо не замкнут и не открыт;

б) оба промежутка являются замкнутыми и ограничеными;

в) оба промежутка открыты.

20. Доказать, что следующие подпространства евклидова пространства гомеоморфны:

а) (n – 1)-мерная сфера и граница замкнутого n-мерного куба, лежащего в ;

б) замкнутый n-мерный куб и замкнутый n-мерный шар.

21. Пусть S – n-мерная сфера с евклидовой топологией на ней, . Доказать, что евклидово пространство и открытый n-мерный шар, лежащий в , гомеоморфны «проколотой сфере».

22. Доказать, что любые два непустых открытых выпуклых подмножества евклидова пространства гомеоморфны, а если эти подмножества являются ограниченными, то их границы также гомеоморфны.

Можно ли утверждать, что любые два замкнутых выпуклых подмножества евклидова пространства , имеющих внутренние точки, гомеоморфны?

23. Доказать, что следующие подпространства евклидовой плоскости гомеоморфны друг другу:

1) «проколотая евклидова плоскость» ;

2) «проколотый открытый круг» .

3) «открытое кольцо» .

24. Доказать, что следующие подпространства евклидова пространства гомеоморфны «проколотой евклидовой плоскости»:

1) «открытый круговой цилиндр», т.е. поверхность, полученная вращением в открытого промежутка (ограниченного или неограниченного) вокруг оси, параллельной этому промежутку;

2) однополостный гиперболоид;

3) дважды проколотая сфера (т.е. теоретико-множественная разность сферы и множества, состоящего из двух точек, принадлежащих этой сфере).

25. Пусть T – тор в (т.е. поверхность, полученная вращением вокружности вокруг оси, лежащей в плоскости этой окружности, но не пересекающей окружность),S₁ – меридиан тора (например, окружность, при вращении которой получен тор), а S₂ – параллель тора T (например, один из экваторов тора). Может ли топологическое преобразование тора T отображать S₁ на S₂, а S₂ − на S₁?

26. Доказать, что каждое топологическое преобразование граничной сферы замкнутого n-мерного шара, лежащего в , можно продолжить до топологического преобразования этого шара.

27. Указать негомеоморфные топологические пространства, содержащиеся в евклидовой прямой , каждое из которых гомеоморфно подпространству другого.

28. Даны следующие отображения евклидовой плоскости в себя:

1)

2)

3)

4)

5)

6)

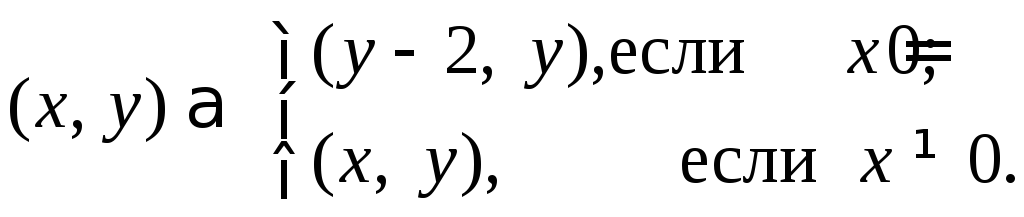
7)

8)

Для каждого из этих отображений укажите множество всех точек, в которых отображение непрерывно.

29. Какие из приведенных ниже условий необходимы, а какие достаточны для непрерывности отображения топологических пространств?

1. .

2. .

3. Для каждой точки пространстваи каждой последовательности, сходящейся вк точке, последовательностьсходитсяв к точке .

4. Для всякого всюду плотного подмножества A пространства множество является всюду плотным подмножеством пространства.

5. .

6. .

7. Для каждой точки и любого множестваиз того, что, следует, что.

8. Для каждой точки существует окрестностьточки , которая содержит образ всякой окрестности точки .

9. .

10. .

11. Для всякого открытого подмножества A пространства множество является открытым подмножеством пространства.

12. Для всякого замкнутого подмножества B пространства множествоявляется замкнутым подмножеством пространства.

13. .

14. Для всякого замкнутого подмножества A пространства множество является замкнутым подмножеством пространства.

15. Для всякого открытого подмножества B пространства множествоявляется замкнутым подмножеством пространства.

30. Какие из следующих утверждений справедливы?

1. Непрерывный образ T₂-пространства – T₂-пространство.

2. Непрерывный образ нормального пространства – нормальное пространство.

3. Непрерывный образ сепарабельного пространства сепарабелен.

4. Непрерывный образ пространства со счетной базой имеет (не более чем) счетную базу.

31. Пусть отображения ипространстваX в евклидову прямую непрерывны в точке , . Определим отображенияравенствами

Доказать: ,непрерывны в точкеa; если же , тонепрерывно в точкеa.

32. Пусть . Определим отображениеевклидовой прямой в евклидово пространство, для каждогополагая

.

Доказать, что непрерывно, замкнуто, но не открыто.

33. Пусть для каждого отображениенепрерывно в точке евклидовой прямой . Определим отображения

, ∆∆

следующими равенствами:

,

∆∆.

Докажите, что непрерывно в точке, а если, то ∆∆непрерывно в точке.

Верно ли, что и ∆∆– открытые (соответственно, замкнутые) отображения, если каждое из отображений , … , открыто (соответственно, замкнуто)?

34. Доказать, что отображение евклидовой плоскостина евклидову прямуюнепрерывно, открыто, но не замкнуто.

35. Каждое ли непрерывное замкнутое отображение одного пространства на другое пространство является открытым?

36. Пусть и – непрерывные отображения топологических пространств и. Доказать, что если отображение открыто (соответственно, замкнуто), то отображениеоткрыто (соответственно, замкнуто).

37. Доказать что отображение f пространства X в пространство Y замкнуто тогда и только тогда, когда любого множества A пространства X выполняется включение .

38. Пусть f – взаимно однозначное отображение пространства X на пространство Y. Доказать, что следующие условия попарно эквивалентны.

1. f – гомеоморфизм.

2. f – непрерывное открытое отображение.

3. f – непрерывное замкнутое отображение.

4. f и – непрерывные отображения.

5. Для любого подмножества A пространства X выполняется равенство .

39*. Указать негомеоморфные топологические подпространства евклидовой прямой , каждое из которых непрерывно и взаимно однозначно отображается на другое.

40. Подмножества A и B пространства X называются функционально отделимыми, если существует непрерывное отображение , для которого,. Доказать:

1. Если любые два замкнутых непересекающихся подмножества T₁-пространства функционально отделимы, то пространство нормально.

2*. Любые два замкнутых непересекающихся подмножества нормального пространства функционально отделимы.

41. Пусть – метрическое пространство. Доказать:

1. Для любого отображение, заданное равенством, непрерывно. При этомтогда и только тогда, когда.

2. Любые два замкнутых непересекающихся подмножества A и B пространства функционально отделимы непрерывным отображением, заданным равенством

.

3*. Если h – непрерывное отображение замкнутого подпространства A пространства в отрезокевклидовой прямой, то отображение, определенное равенством

,

непрерывно и при этом .

42*. Доказать, что регулярное пространство со счетной базой метризуемо.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Введение в топологию : учебн. пособие / Ю.Г. Борисович [и др.]. – М. : Наука, 1995. – 416 с.

1. Дифференциальная геометрия, топология, тензорный анализ : сб. задач / Н.И. Кованцов [и др.]. – К. : Выща шк., 1989. – 398 с.

2. Келли Дж.Л. Общая топология / Дж.Л. Келли. – М. : Наука, 1981. – 432 с.

3. Мищенко А.С. Курс дифференциальной геометрии и топологии : учебн. пособие / А.С. Мищенко, А.Т. Фоменко. – СПб. : Лань, 2009. – 480 с.

4. Топология : учебн. пособие / С.Г. Кононов [и др.]. ; под общ. ред. А.С. Феденко – Минск: Выш. шк., 1990. – 318 с.

Методические указания к практическим занятиям по курсу

«Дифференциальная геометрия и топология»

раздел «Топология»

для студентов 3 курса дневной формы обучения

направления подготовки 6.040201 «математика»

образовательно-квалификационного уровня «бакалавр»

отрасли знаний 0402 «физико-математические науки»

Составитель: Криворучко Александр Иванович

Рецензент: М.А.Муратов

Редактор: Н.А.Василенко

_________________________________________________________

Подписано к печати . .11. Формат 60x84/16. Бумага тип. ОП.

Объем 1,5 п. л. Тираж - 50. Заказ -

_________________________________________________________