Вопросы для повторения
Что такое топология?
Является ли промежуток ]0; 1[ числовой прямой открытым множеством? Является ли этот промежуток открытым на числовой евклидовой прямой? Будет ли этот же промежуток открытым (или замкнутым) на дискретной числовой прямой?
Может ли пересечение конечного семейства открытых множеств топологического пространства не быть открытым? Может ли пересечение бесконечного семейства открытых множеств топологического пространства не быть открытым?
Является ли точка 0 на числовой прямой R бесконечно близкой к интервалу ]0; 1[ ?
Метризуема ли числовая прямая?
Приведите пример неметризуемого топологического пространства.
Иногда говорят, что «метрические пространства – частный случай топологических пространств». Верно ли это?
Может ли замыкание интервала ]0; 1[ числовой прямой R совпадать с R?
Может ли одноточечное подмножество бесконечного топологического пространства быть всюду плотным?
Может ли точка прикосновения множества не быть его предельной точкой?
Может ли предельная точка множества не быть его точкой прикосновения?
Может ли точка прикосновения множества A иметь окрестность, содержащую только одну точку множества A ?
Может ли предельная точка множества A иметь окрестность, содержащую только одну точку множества A ?
Пусть
– метрическое пространство,
,
.
Можно ли утверждать, что, что
тогда и только тогда, когда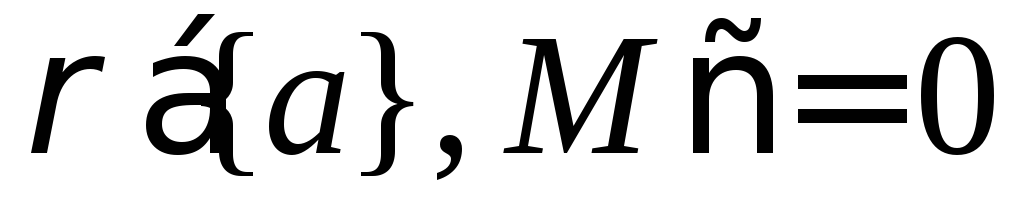
?Может ли множество строго содержаться в его границе?
Пусть
– последовательность точек
пространстваX.
Что означает равенство
?Следующие понятия являются топологическими: окрестность, замкнутое множество, предельная точка, граничная точка, дискретное пространство, метризуемое пространство, и т.д. Что это означает? Является ли метрика топологическим понятием?
Задания
1.
Пусть x,
y,
z
попарно различны. В каком случае
упорядоченная пара
является топологическим пространством?
а)
,
;
б)
,
;
в)
,
;
г)
,
.
2. Доказать:
а) единичное отображение idX топологического пространства X на себя является гомеоморфизмом;
б) отображение, обратное гомеоморфизму топологического пространства − гомеоморфизм;
в) если
и
– гомеоморфизмы топологических
пространств, то композиция
этих гомеоморфизмов также является
гомеоморфизмом.
3. Доказать:
а) каждое пространство гомеоморфно самому себе;
б) если пространство X гомеоморфно пространству Y, то Y гомеоморфно X;
в) если пространство X гомеоморфно пространству Y, а Y гомеоморфно пространству Z, то X гомеоморфно Z.
4. Пусть U – подмножество пространства X. Доказать, что следующие условия попарно эквивалентны:
а) U открыто в X;
б) для каждой точки множества U найдется окрестность этой точки, содержащаяся в U;
в)
замкнуто вX;
г) U – дополнение некоторого замкнутого подмножества пространства X;
д)
.
5. Доказать, что в топологическом пространстве
а) множество всех точек пространства и пустое множество замкнуты;
б) пресечение любого семейства замкнутых множеств является замкнутым множеством;
в) объединение любого конечного семейства замкнутых множеств замкнуто.
6. Пусть H – подмножество пространства X. Доказать, что каждое из следующих условий эквивалентно замкнутости H:
а) H – дополнение в X некоторого открытого подмножества пространства X;
б) каждая точка, бесконечно близкая к H, принадлежит H;
в)
.
7.
Пусть a
– точка
пространства X,
.
Доказать, что каждое из следующих условий
эквивалентно тому, что
:
а) точка a бесконечно близка к H;
б) либо
,
либоa
– предельная точка множества H.
8. Доказать, что замыкание пустого подмножества топологического пространства пусто; при этом для любых подмножеств A и B топологического пространства
,
,
.
9.
Пусть X
– топологическое пространство,
,
.
Используя определение замыкания
множества, доказать:
а)
;
б)
;
в) если
,
то
;
г)
X
= X.
Можно ли утверждать,
что
?
10.
Пусть
– семейство подмножеств пространстваX.
Используя определение замыкания
множества, доказать, что
,
.
Можно ли утверждать,
что
?
11. Доказать, что свойства замыкания, указанные в заданиях 9 и 10, следуют из свойств замыкания, приведенных в задании 8.
12.
Докажите, что для любого счетного
семейства
подмножеств топологического пространства
Существует ли
счетное семейство
,
для которого
?
13.
Пусть множество A
открыто в пространстве X,
.
Доказать, что
тогда и только тогда, когда
.
14.
Пусть множество A
замкнуто в
пространстве X,
а множество B
открыто
в X.
Доказать, что
замкнуто, а
открыто вX.
15.
Пусть A
и B
– подмножества топологического
пространства, A
открыто и
.
Доказать, что
.
16. Доказать, что подмножество A топологического пространства замкнуто тогда и только тогда, когда каждая предельная точка этого подмножества принадлежит A.
17.
Доказать, что точка a
подмножества A
топологического пространства является
изолированной точкой этого подмножества
тогда и только тогда, когда точки a
имеет окрестность U,
для которой
.
18.
Привести пример пространства X,
в котором некоторая точка x
является предельной для множества
,
но никакая последовательность точек,
принадлежащих
,
не сходится к точкеx.
19.
Пусть x
– точка пространства X.
Можно ли утверждать, что если x
– предельная
точка для множества
,
тоx
– предельная
точка некоторой последовательности
точек, принадлежащих
?
20.
Пусть
– последовательность точек метрического
пространства
.
Доказать:
а) эта последовательность имеет не более одного предела;
б) (
)
(
).
21.
Даны следующие семейства подмножеств
вещественной прямой
:
1.
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
.
8.
.
9.
.
10.
.
11.
.
12.
.
13.
.
14.
.
15.
.
Какие из них являются топологиями на множестве R?
Для какой из этих топологий
а) Q открыто?
б) Q замкнуто?
в)
открыто?
г)
замкнуто?
д)
открыто?
е)
замкнуто?
22.
Даны подмножества евклидовой плоскости
:
1.
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
.
8.
9.
.
10.
.
11.
.
12.
.
13.
.
14.
.
15.
.
16.
.
Для каждого из этих множеств найти его внутренность, замыкание и границу. Какие из этих множеств открыты? Какие из этих множеств замкнуты? Какие из этих множеств всюду плотны?
23. Какие из следующих условий достаточны, а какие необходимы для того, чтобы подмножество A пространства X было открытым?
A не замкнуто в X.
Ни одна точка множества Fr A не принадлежит A.
Каждая точка прикосновения множества A ему принадлежит.
Всякая точка прикосновения множества A является его граничной точкой.
Множество A содержит все свои внутренние точки.
Всякая граничная точка множества A является его точкой прикосновения.
24. Какие из следующих условий необходимы, а какие достаточны для того, чтобы подмножество A пространства X было замкнутым?
Всякая точка, не являющаяся точкой прикосновения множества A, ему не принадлежит.
Для каждой последовательности точек множества A всякий предел в X этой последовательности принадлежит A.
Для каждой последовательности точек множества A всякая предельная в X точка этой последовательности принадлежит A.
Для всякой точки
,
если некоторая окрестность точкиx
пересекает A,
то
.Множество A не открыто.
25. Какие из следующих условий необходимы, а какие достаточны для того, чтобы подмножество A пространства X было всюду плотным?
Множество A не открыто.
Множество A не замкнуто.
Для каждого непустого открытого подмножества U пространства X множество
пусто.Найдется граничная точка множества A, которая ему не принадлежит.
26. Какие из следующих утверждений справедливы для каждого подмножества A любого топологического пространства X ?
1.
.
2.
.
3.
.
4.
.
5.
.
6. Если A
− конечное множество, то
.
7. Если A
и
,
то
.
8. Если A
открыто, то
.
9. Если
,
тоA
замкнуто.
10. Если
конечно, то
.
11. Если A
плотно в X,
то
.
12. Если
,
то
.
13.
.
14.
.
15.
.
16.
.
17.
.
18.
.
19.
.
20.
.
21.
.
22.
.
23.
.
24.
.
25.
.
26.
.
27. Какие из следующих утверждений справедливы для любых подмножеств A и B произвольного пространства X ?
1.
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
.
8.
.
9.
.
10.
.
11.
.
12.
.
13.
.
14.
.
15.
.
16.
.
17.
.
18.
.
19.
.
20.
.
21.
.
22.
.
30. Если A
и
B
– всюду
плотные подмножества, то
всюду плотно.
31. Если A
и
B
– всюду плотные подмножества, и хотя
бы одно из этих подмножеств открыто, то
всюду плотно.
32. Если A
и
B
– всюду
плотные подмножества, и хотя бы одно из
этих подмножеств замкнуто, то
всюду плотно.
33. Если A
открыто, а
B
всюду плотно,
то
.
34. Если A
замкнуто, а
B
всюду плотно, то
.
35. Если B
всюду плотно и открыто, то
.