
- •Курсовая работа
- •Содержание
- •Введение
- •Нелинейные динамические модели
- •Выбор оптимального решения на основе классификации экономико-математических моделей
- •Биография
- •Логистическое уравнение
- •Логистическое отображение
- •Зависимость поведения от параметра
- •Аналитическое решение
- •Модель Ферхюльста (рождаемость и смертность с учетом роста численности)
- •Для этой модели нужно взять побольше временной диапазон ,т.К. Она наглядна на длинном промежутке времени временной диапазон ,т.К. Она наглядна на длинном промежутке времени. Динамика Ферхюльста
- •Гиперболический рост населения земли и модель с.П. Капицы
- •Модель роста населения земли и технологии м. Кремера
- •Модель роста жизнесберегающих технологий а.В. Подлазова
- •Миф о том, что синергетика может объяснить гиперболический рост численности населения Земли
- •Заключение
- •Список использованных источников:
Логистическое уравнение
Логистическое уравнение, также известное, как уравнение Ферхюльста (по имени впервые сформулировавшего его бельгийского математика), изначально появилось при рассмотрении модели роста численности населения.
Исходные предположения для вывода уравнения при рассмотрении популяционнойдинамики выглядят следующим образом:
скорость размножения популяции пропорциональна её текущей численности, при прочих равных условиях
скорость размножения популяции пропорциональна количеству доступных ресурсов, при прочих равных условиях. Таким образом, второй член уравнения отражает конкуренцию за ресурсы, которая ограничивает рост популяции.
Обозначая
через ![]() численность
популяции (вэкологиичасто
используется обозначение
численность
популяции (вэкологиичасто
используется обозначение![]() ),
а время —
),
а время —![]() ,
модель сводится кдифференциальному
уравнению:
,
модель сводится кдифференциальному
уравнению:
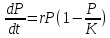
где
параметр ![]() характеризует
скорость роста (размножения), а
характеризует
скорость роста (размножения), а![]() —
поддерживающую ёмкость среды (то есть,
максимально возможную численность
популяции). Исходя из названия
коэффициентов, вэкологиичасто
различают
две стратегии поведения видов:
—
поддерживающую ёмкость среды (то есть,
максимально возможную численность
популяции). Исходя из названия
коэффициентов, вэкологиичасто
различают
две стратегии поведения видов:
 -стратегия
предполагает бурное размножение и
короткую продолжительность жизни
особей
-стратегия
предполагает бурное размножение и
короткую продолжительность жизни
особейа
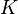 -стратегия
— низкий темп размножения и долгую
жизнь.
-стратегия
— низкий темп размножения и долгую
жизнь.
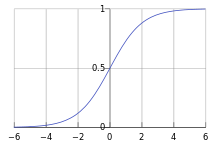
![]() Рис.2
Рис.2
Логистическая кривая для K=1 иP0=0,5
Точным
решением уравнения (где ![]() —
начальная численность популяции)
являетсялогистическая
функция,
S-образная кривая, (логистическая кривая):
—
начальная численность популяции)
являетсялогистическая
функция,
S-образная кривая, (логистическая кривая):

где
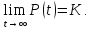
Ясно, что в ситуации «достаточного объёма ресурсов», то есть пока P(t) много меньше K, логистическая функция поначалу растёт приблизительно экспоненциально:
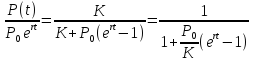
Аналогично, при «исчерпании ресурсов» (t → ∞) разность K-P(t) экспоненциально убывает с таким же показателем.
Почему Ферхюльст назвал уравнение логистическим, остается неизвестным. В 1924году Раймонд Перл применил уравнение для описанияавтокаталитических реакций.
Дискретным аналогом логистического уравнения является логистическое отображение.
Логистическое отображение
[6] Логистическое отображение(такжеквадратичное отображениеилиотображение Фейгенбаума) — этополиномиальноеотображение, которое описывает, как меняется численностьпопуляциис течением времени. Его часто приводят в пример того, как из очень простыхнелинейных уравненийможет возникать сложное,хаотическоеповедение. Логистическое отображение —дискретныйаналог непрерывногологистического уравненияФерхюльста; оно отражает тот факт, что прирост популяции происходит в дискретные моменты времени.
Математическая формулировка отображения
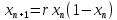
где:
![]() принимает
значения от 0 до 1 и отражает численность
популяции в n-ом
году, а
принимает
значения от 0 до 1 и отражает численность
популяции в n-ом
году, а  обозначает
начальную численность (в год номер 0);
обозначает
начальную численность (в год номер 0);
![]() —положительный
параметр, характеризующий скорость
размножения (роста) популяции.
—положительный
параметр, характеризующий скорость
размножения (роста) популяции.
Иногда эта формулировка называется отображением Ферхюльста (или Ферхюльста-Пирла), а логистическим отображением называется другая, но эквивалентная по свойствам формула:

Это нелинейное отображение описывает два эффекта:
с одной стороны, когда численность популяции мала, она размножается со скоростью, пропорциональной этой численности;
с другой стороны, поскольку популяция обитает в среде с ограниченной «ёмкостью», то при росте плотности популяции скорость размножения падает, возрастает конкуренция и смертность.
Одним из недостатков использования отображения в качестве демографическоймодели является тот факт, что при некоторых начальных значениях и величинах параметров отображение даёт отрицательные значения численности популяции. Этого недостатка лишена дискретнаямодель Рикера, которая также демонстрирует хаотическое поведение.
