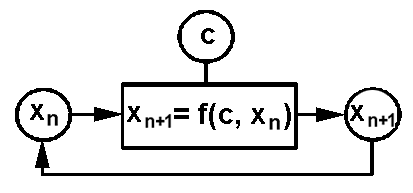Модель Ферхюльста (рождаемость и смертность с учетом роста численности)

Постановка задачи [4] Как правило, численность популяции зависит не только от рождаемости и смертности, но и от ограниченности пищевых и других ресурсов. Вскоре за созданием модели Мальтуса, бельгийский математик Ферхюльст задался вопросом: будет ли население Бельгии расти неограниченно? Ответом на этот вопрос было создание новой модели динамики численности популяции при ограниченных ресурсах, описываемая следующим уравнением: dN/dt=r*N-m*N²(1)  r - удельная скорость роста численности N - численность популяции m - число встреч членов популяции, при котором они могут конкурировать за какой-либо ресурс уравнение это отличается от уравнения экспотенциального роста (уравнения Мальтуса) выражением m*N2, которое как раз и отражает ограниченность ресурсов. Перепишем уравнение так: dN/dt=N(r-m*N) Выражение в скобках - это удельная скорость роста популяции. Причем чем больше численность популяции (N), тем меньше скорость роста. Если в правой части уравнения вынести за скобки выражение r  dN/dt=N*r(1-N*m/r)  и обозначить m/r за 1/K, то уравнение можно переписать так: dN/dt=N*r(1-N/K) При малых N значением N/K можно пренебречь, и тогда рост численности идет по экспоненциальному закону, при возрастании N и неизменном K рост численности будет замедляться, и приN близком к К рост остановится. Величину К называют емкостью среды. Она отражает возможности среды обитания предоставить популяции нужные для ее роста ресурсы.  Уравнение графически отображается в виде S- образной кривой. Эта кривая называется логистической кривой, а рост численности ,соответствующий уравнению - логистическим. Исследуя кривую, можно сказать , что максимальная скорость роста достигается , когда численность равна K/2. В некоторый момент численность стабилизируется и остается постоянной величиной. Популяции, существующие в условиях ограниченных ресурсов, часто хорошо подчиняются правилам логистического роста. Например, когда овцы были завезены в Тасманию, рост их стада описывался логистической кривой. Но правила логистического роста приложимы не ко всем случаям. Например, у размножающихся половым путем видов, при слишком малой численности мала вероятность встреч особей разного пола и размножение может вообще прекратиться.  Для реализации модели в среде электронных таблиц уравнение следует представить в дискретном виде N(i+1)=N(i)*r*(1-N(i)/K) где N(i) - численность популяции в i-й момент времени; r -удельная скорость роста популяции (рождаемость/ смерность); К - емкость среды

Компьютерная модель 4

	A	B	C	D	E	F
1	Коэффициент  рождаемости 14,5	Коэффициент смертности 10,2	Начальная  численность 147000000	Емкость среды К (7350000000)	Удельная скорость роста =$A$1/$B$1
2	0 0	=A2+1 1	=B2+1 2	=C2+1 3	=D2+1	...
3	=c$1 1000	=A3*$E$1*(1 - A3/$D$1)	Копировать формулу из B3	...	...	...

Для этой модели нужно взять побольше временной диапазон ,т.К. Она наглядна на длинном промежутке времени временной диапазон ,т.К. Она наглядна на длинном промежутке времени. Динамика Ферхюльста

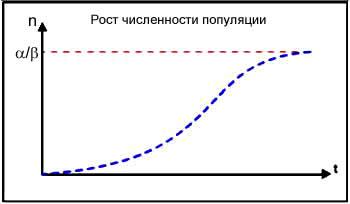
[5] В качестве модели в данной работе используется уравнение Ферхюльста, предложенное им в 1845 г. и описывающее динамику роста численности популяции организмов. Как было выяснено позднее (более чем через сто лет), это уравнение носит принципиальный характер, и предсказанные им сценарии были обнаружены при описании некоторых свойств турбулентного потока, а также в исследованиях по лазерной физике, гидродинамике и кинетике химических реакций. Уравнение Ферхюльста описывает изменение численности n популяции от времени и в дифференциальной форме выглядит следующим образом: dn/dt = αn - βn² , где в правой части 1-е выражение соответствует количеству рождений, а 2-е количество смертей. При некой начальной численности n, не равной нулю, популяция будет расти до определенного максимального значения N_max= α/β (Рис. 4). Это значение называют емкостью среды.

Рис.4

Однако запись уравнения Ферхюльста в дифференциальной форме, подразумевает, что значения dn и dt могут быть сколь угодно малыми. А реально dn не может быть меньше чем одна особь, а dt меньше, чем минимальное время воспроизводства. Т.е. эти величины дискретны. Поэтому уравнение Ферхюльста правильнее записать в численном виде.

Пусть N₀ - начальная численность популяции. Через год ее численность станет равна N₁, а через n лет - N_n. Через n+1 станет равной N_n+1 и так далее. Однако в реальных условиях численность популяции не может расти бесконечно, и есть некоторое максимальное значение N_max, которое определяется количеством особей способных прокормиться на территории их обитания. Если количество особей превышает это значение, численность популяции убывает, если меньше - возрастает. При построении моделей используют не абсолютные значения N_n, а относительную величину: x_n = N_n/ N_max, тогда x_max = N_max/ N_max = 1. Коэффициент прироста популяции R определяется как относительное изменение численности: 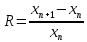.Чтобы популяция бесконечно не увеличивалась, коэффициент R должен, с приближением к N_max (x_n = 1), уменьшаться до 0. Тогда можно записать: 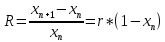 Из этого можно вывести,уравнение Ферхюльста. 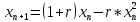Оно описывает динамику роста численности популяции, и представляет собой нелинейное уравнение следующего вида: Где x_n - численность популяции через n лет, x_n+1 - на последующий год, r - параметр роста. Первое выражение в правой части уравнения - равно приросту численности популяции, а второе - ее убыли.

Анализ динамики роста численности популяции заключается в исследовании изменения численности особей во времени при разных значениях параметра роста r. Для этого используются соответствующие программы, позволяющие последовательно рассчитать, на основании уравнения Ферхюльста, численность популяции от начального значения x₀ до значения в n-й год x_n. При подстановке в правую часть уравнения x₀ сначала находится x₁, затем по x₁ находится x₂, и так далее... Уравнение Ферхюльста является частным случаем процесса с обратной связью, в котором одна и та же операция выполняется снова и снова, и результат одной операции является начальным значением для следующей (Рис.5).

Риc.5

Единственное, что требуется, чтобы динамический закон x_n+1 = f(x_n) был более сложным, чем простая пропорциональность x_n+1 = kx_n. На рисунке c является параметром, от которого зависит этот динамический закон. Изучение динамики роста, в зависимости от параметра роста показывает, что она существенно сложней, чем приведенная на рисунке 1.8. При определенных значениях этого параметра возникает колебательный режим, затем усложнение характера колебаний вплоть до не предсказуемой хаотической динамики. Такая хаотическая динамика называется динамическим хаосом. Динамический хаос в отличие от теплового хаотического движения детерминирован: он имеет структуру и в его основе лежит строгое математическое выражение. Точки перехода от одного характера динамики к другому имеют специфическое название - бифуркации. Кроме этого, оказалось, что диаграмма, отражающая возможный характер динамики в зависимости от параметра роста (сценарий Ферхюльста) является фрактальной структурой.