Lektsii_Rubleva_1 / Гл 08 Кратн_ кривол_н_йн_ та поверхнев_ _нтеграли / Пар 8-15 Формула Гаусса-Остроградського

3

Глава 8

Кратні, криволінійні та поверхневі інтеграли

15. Формули Гауса-Остроградського та Стокса

Скінчена лінійна комбінація простих регулярних орієнтованих поверхонь з класу з цілими коефіцієнтами називається ланцюгом з того самого класу і позначається символом .

Покладемо за означенням: 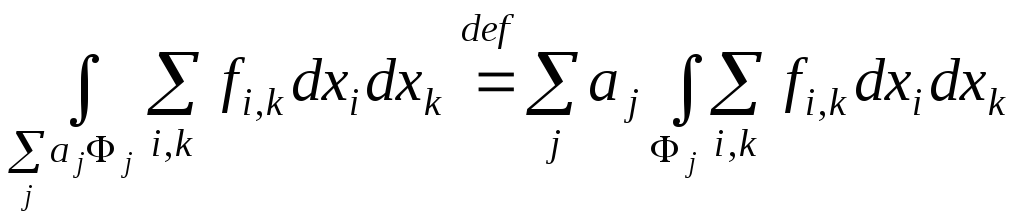, кожного разу як тільки права частина існує.

Тіло називається елементарним для інтегрування по першій та другій змінним, якщо існують елементарна множина та функції такі, що .

З геометричної точки зору вказане тіло обмежене зверху графіком функції (поверхнею) , знизу - , а з боків – циліндричною поверхнею, твірні якої паралельні осі . Межу тіла розуміємо як ланцюг, складений з орієнтованої поверхні (її параметричне зображення має вигляд , ), яка береться з множником „”, орієнтованої поверхні (її параметричне зображення має вигляд , ), яка береться з множником „” та циліндричної поверхні , орієнтованої так, що відповідна нормаль направлена зовні тіла з множником „”. Цей ланцюг будемо називати додатною межею тіла . Розглянемо тепер вектор-функцію . Треба обчислити поверхневий інтеграл другого роду: . Розіб’ємо цей інтеграл на суму трьох інтегралів по відповідних поверхнях. З того, що на циліндричній поверхні вектор нормалі має вигляд , то підінтегральний вираз дорівнює: , а тому

.

Повністю аналогічно визначаються тіла, що є елементарними для інтегрування по інших парах змінних.

Тіло називається елементарним, якщо його можна подати у вигляді скінченого об’єднання тіл, без спільних внутрішніх точок, які є елементарними для інтегрування по -й та -й змінним. Додатною межею тіла є сума ланцюгів, що утворюють додатні межі складових тіл.

Теорема 1.	(Гауса-Остроградського)
	Нехай - елементарне тіло в просторі , - його додатна межа. Якщо функція , то

Доведення. Потрібно довести три аналогічні формули, а тому доведемо одну з них: . Згідно теореми Фубіні та формули Ньютона-Лебніца, маємо:

, що й треба було довести.

Теорема доведена.

Наслідок.	(Обчислення об’єму за допомогою поверхневого інтегралу)
	Об’єм - елементарне тіла в просторі , можна обчислити за допомогою поверхневого інтегралу 2-го роду за однією з формул: , де - його додатна межа.

Все слідує з формули Гауса-Остроградського, якщо зробити так, щоб підінтегральна функція в потрійному інтегралі була одиниця.

Теорема 2.	(Стокса)
	Нехай - проста гладка орієнтована поверхня в просторі , - неперервна на функція разом із своїми похідними . Тоді має місце формула Стокса: , де - орієнтована межа поверхні ; , - оператори диференціювання, - вектор нормалі до поверхні .

Доведення. Нехай поверхню, яка складається з об’єднання простих поверхонь

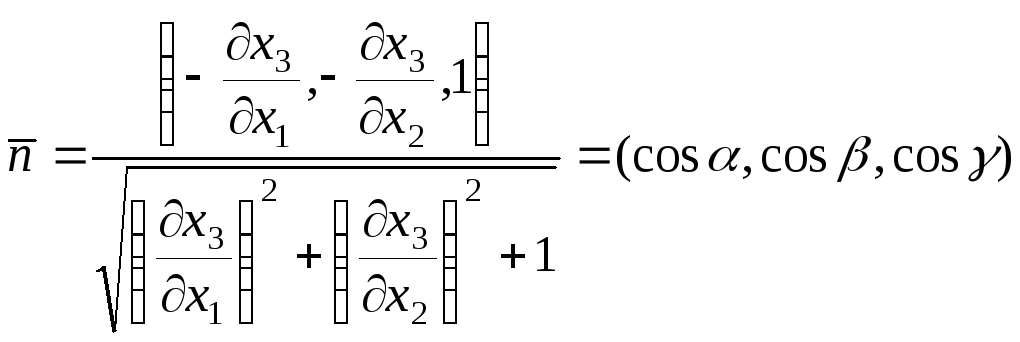ми можемо подати у явному вигляді рівнянням , де , - відповідно орієнтована межа компакту . Розглянемо криволінійний інтеграл: (за формулою Гріна) . Вектор нормалі дорівнює: , а тому , , .

Аналогічно доводяться для інших доданків.

Теорема доведена.
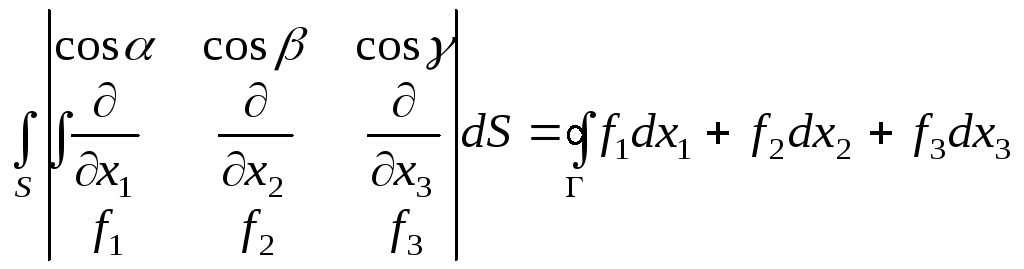