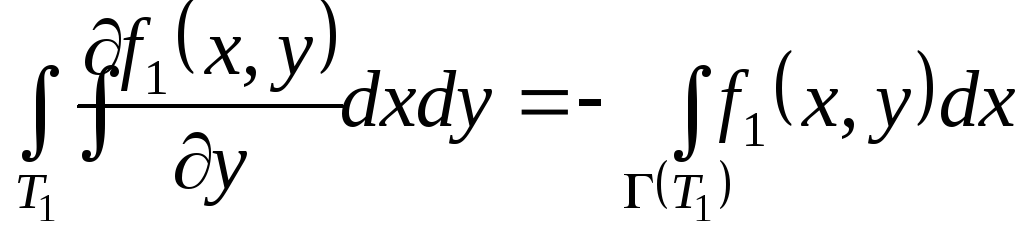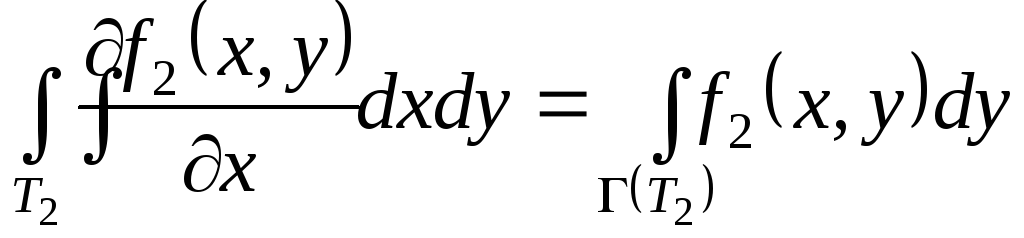Lektsii_Rubleva_1 / Гл 08 Кратн_ кривол_н_йн_ та поверхнев_ _нтеграли / Пар 8-11 Формула Гр_на

2

Глава 8

Кратні, криволінійні та поверхневі інтеграли

11. Формула Гріна

Функція називається кусково-гладкою, якщо існує таке розбиття сегмента , що звуження є неперервно диференційованими функціями.

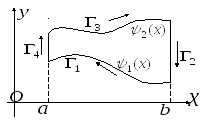
Множина називається криволінійною трапецією першого роду, якщо та - кусково-гладкі функції, що визначені на сегменті .

Нехай гладкі орієнтовані криві з параметричними зображеннями , де:

, ,

, ,

, ,

, .

Упорядкований набір називається додатно орієнтованою межею трапеції . Указану межу називають орієнтованою проти руху годинникової стрілки.

Теорема 1.	(Гріна, для трапецій першого роду).
	Нехай функції , і неперервні. Тоді
		(1)

Доведення.

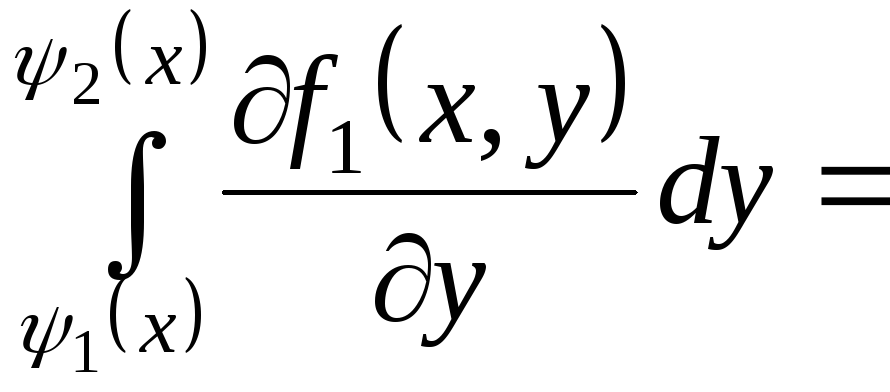
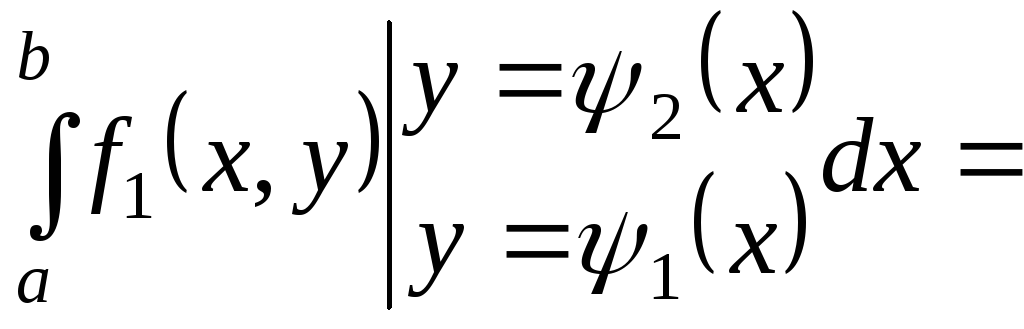
Теорема доведена.

Повністю аналогічно визначається трапеція другого роду . При цьому додатна орієнтація буде відповідати руху годинникової стрілки. Додатною орієнтацією будемо вважати ту, яка протилежна рухові годинникової стрілки. В зв’язку з цим аналог формули (1) приймає вигляд:

(2)

(треба змінити знак правої частини).

Множина називається елементарною, якщо прямими, паралельними координатним осям, її можна розбити на скінчену кількість трапецій першого і другого роду.

Межею елементарної множини є кусково-гладка крива і ми орієнтуємо її проти годинникової стрілки.

Теорема 2.	(Гріна, для елементарних множин).
	Нехай - елементарна множина. Якщо функція неперервна разом з частинними похідними і на множині , то виконується рівність:
		(3)

Це випливає з означення елементарної множини та формул (2.1), (2.2).

Наслідок.	(Обчислення площі за допомогою криволінійних інтегралів)
	Нехай - елементарна множина, межа якої проста замкнена крива без само перетинів та пробігається в додатному напрямі. Тоді площу області можна обчислити за однією з формул:
		(4)

Доведення теореми слідує з формули Гріна та формули обчислення площі через подвійний інтеграл:

.