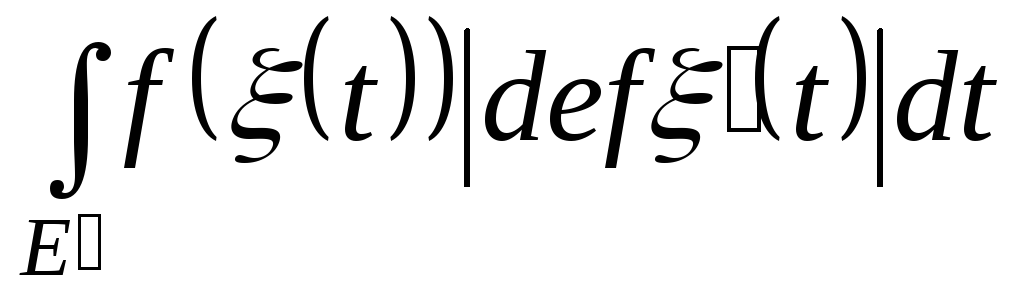Lektsii_Rubleva_1 / Гл 08 Кратн_ кривол_н_йн_ та поверхнев_ _нтеграли / Пар 8-09 Невласний _нтеграл Р_мана
.doc
Глава 8
Кратні, криволінійні та поверхневі інтеграли
9.
Невласний
![]() -
кратний інтеграл Рімана
-
кратний інтеграл Рімана
Точка
![]() називається особливою
точкою
для інтегрування функції
називається особливою
точкою
для інтегрування функції
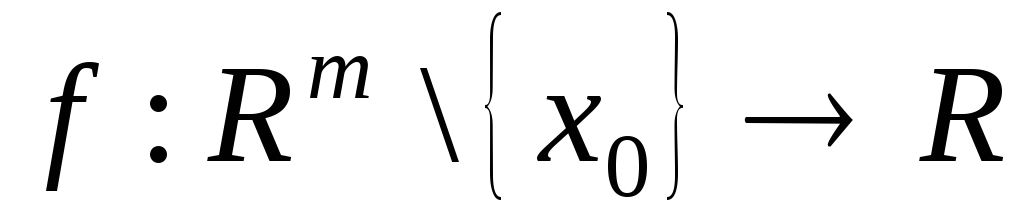 (
(![]() ),
якщо
),
якщо
![]() не обмежена в будь-якому її околі
не обмежена в будь-якому її околі
![]() .
.
Припустимо,
що всі особливі точки функції
![]() утворюють замкнену множину
утворюють замкнену множину
![]() міри
міри
![]() (можливо
(можливо
![]() ).
Візьмемо послідовність множин
).
Візьмемо послідовність множин
![]() ,
яка має властивості:
,
яка має властивості:
1)![]() відкриті
відкриті
![]() та вимірні за Жорданом (межа такої
множини має міру 0);
та вимірні за Жорданом (межа такої
множини має міру 0);
2)![]() і
і
![]()
![]()
![]() .
.
Таку
послідовність множин назвемо припустимою
для інтегрування функції
![]() з множиною особливих точок
з множиною особливих точок
![]() ,
або коротше – припустимою.
,
або коротше – припустимою.
(Зазначимо, що з вимірності за Жорданом слідує їх обмеженість).
Нехай
![]() неперервна майже скрізь в області
визначення, оскільки
неперервна майже скрізь в області
визначення, оскільки
![]() і
і
![]()
![]() ,
то у кожної точки
,
то у кожної точки
![]()
![]() є окіл
є окіл
![]() ,
значення функції в якому обмежені. За
теоремою Гейне-Бореля, з вказаної сім’ї
околів можна вибрати їх скінчену
підмножину
,
значення функції в якому обмежені. За
теоремою Гейне-Бореля, з вказаної сім’ї
околів можна вибрати їх скінчену
підмножину
![]()
![]() ,
яка покриває
,
яка покриває
![]() .
Тоді в кожному з околів
.
Тоді в кожному з околів
![]() обмежена числом
обмежена числом
![]() ,
тоді числом
,
тоді числом
![]()
![]() функція обмежена на множині
функція обмежена на множині
![]() ,
звідси вона інтегрована на множині
,
звідси вона інтегрована на множині
![]() .
.
Розглянемо
послідовність
![]() кратних
інтегралів Рімана
кратних
інтегралів Рімана
![]() . (1)
. (1)
Якщо
для будь-якої припустимої послідовності
множин (![]() )
послідовність інтегралів Рімана (
)
послідовність інтегралів Рімана (![]() )
має при
)
має при
![]() скінчену границю
скінчену границю
![]() ,
яка не залежить від вибору припустимої
послідовності, то існує
(збігається) невласний
,
яка не залежить від вибору припустимої
послідовності, то існує
(збігається) невласний
![]() кратний
інтеграл Рімана:
кратний
інтеграл Рімана:
![]() , (2)
, (2)
який
дорівнює числу
![]() .
Якщо
.
Якщо
![]() ,
або взагалі не існує, то невласний
інтеграл (2) не існує (розбігається).
,
або взагалі не існує, то невласний
інтеграл (2) не існує (розбігається).
Невласний
інтеграл (10.2) називається абсолютно
збіжним,
якщо збігається інтеграл![]() .
.
|
Теорема 1. |
(Невласний інтеграл для невід’ємної функції) |
|
|
Нехай
функція |
Доведення.
Існування границі послідовностей
(скінченої чи нескінченої) за будь-якого
вибору припустимої послідовності множин
(![]() )
випливає з теореми Вейєрштрасса про
границю монотонної числової послідовності.
Залишилося довести незалежність границі
від вибору послідовності (
)
випливає з теореми Вейєрштрасса про
границю монотонної числової послідовності.
Залишилося довести незалежність границі
від вибору послідовності (![]() ).
).
Нехай
(![]() )
– інша припустима послідовність множин.
)
– інша припустима послідовність множин.
![]() замкнена і обмежена і
замкнена і обмежена і
![]()
![]() ,
тому (
,
тому (![]() )
)
![]() покриття
множини
покриття
множини
![]() .
За теореми Гейне-Бореля, з неї можна
виділити скінчене покриття. Тому існує
номер
.
За теореми Гейне-Бореля, з неї можна
виділити скінчене покриття. Тому існує
номер
![]() :
:
![]()
![]() ,
,
![]() .
В нерівності
.
В нерівності
![]()
![]()
![]() (4)
(4)
перейдемо
спочатку до границі при
![]() ,
а далі до границі при
,
а далі до границі при
![]() ,
звідси одержимо:
,
звідси одержимо:
![]()
![]() . (5)
. (5)
Замінюючи
місцями (![]() )
і (
)
і (![]() ),
одержимо нерівність, зворотну до
нерівності (5),
звідси і одержимо бажану рівність.
),
одержимо нерівність, зворотну до
нерівності (5),
звідси і одержимо бажану рівність.
Теорему доведено.
|
Теорема 2. |
(Збіжність абсолютно збіжного інтегралу) |
|
|
Нехай
|
Доведення.
Розглянемо функції
![]() ,
,
![]() .
Вони обидві невід’ємні і, крім того,
виконуються рівності:
.
Вони обидві невід’ємні і, крім того,
виконуються рівності:
![]() ;
;
![]() .
Тому маємо:
.
Тому маємо:
|
|
|
(6) |
|
|
|
(7)
|
де
(![]() )-
довільна припустима послідовність
множин.
)-
довільна припустима послідовність
множин.
З
рівності (6)
слідує обмеженість послідовностей
![]() ,
,
![]() і з теореми 1 обидва ці інтеграли
збігаються:
і з теореми 1 обидва ці інтеграли
збігаються:
![]() ,
,
![]() ,
а з рівності (7)
слідує існування скінченої і незалежної
від припустимої послідовності (
,
а з рівності (7)
слідує існування скінченої і незалежної
від припустимої послідовності (![]() )
границі
)
границі
![]() і існує інтеграл:
і існує інтеграл:
![]()
![]()
![]() .
.
Теорему доведено.
|
Теорема 3. |
(Зв’язок абсолютної та простої збірностей інтегралів) |
|
|
Нехай
|
Доведення.
Припустимо, що збіжний інтеграл (2)
абсолютно розбіжний, тоді для будь-якої
припустимої послідовності множин (![]() )
маємо:
)
маємо:
![]() .
Легко зрозуміти, що можна було взяти
таку послідовність (
.
Легко зрозуміти, що можна було взяти
таку послідовність (![]() ),
для якої
),
для якої
|
|
|
(8) |
Поклавши
![]() ,
дістанемо нерівність:
,
дістанемо нерівність:
![]()
![]() .
Згадуючи, що
.
Згадуючи, що
![]() ,
запишемо останню нерівність у вигляді:
,
запишемо останню нерівність у вигляді:
|
|
|
(9) |
Враховуючи
невід’ємність обох функцій
![]() і
і
![]() ,
маємо, що з двох інтегралів
,
маємо, що з двох інтегралів
![]() і
і
![]() один більше або дорівнює іншому. Нехай
один більше або дорівнює іншому. Нехай
![]()
![]()
![]() .
Тоді з (9)
ми одержимо:
.
Тоді з (9)
ми одержимо:
|
|
|
(10) |
Візьмемо
такий
![]() вимірний
брус
вимірний
брус
![]()
![]()
![]() ,
що
,
що
![]()
![]() ,
де
,
де
 .
.
З
нерівності (10)
ми одержимо:![]()
![]()
![]() ,
з властивості верхньої межі знайдеться
таке розбиття
,
з властивості верхньої межі знайдеться
таке розбиття
![]() ,
що
,
що
|
|
|
(11) |
Нехай
![]() внутрішність тих комірок, в яких функція
внутрішність тих комірок, в яких функція
![]() додатна
додатна
![]()
Тому
маємо:
![]()
![]()
![]() .
Позначимо
.
Позначимо
![]() вона
припустима і
вона
припустима і
![]()
![]()
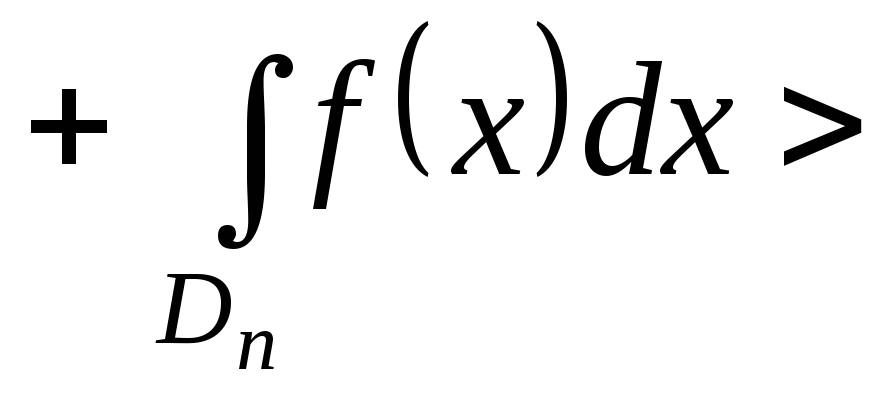
![]() . (12)
. (12)
З
останньої нерівності слідує, що
послідовність
![]() - необмежена (теж саме було б у припущенні
- необмежена (теж саме було б у припущенні
![]()
![]()
![]() ).
).
Теорема доведена.
|
Теорема 4. |
(Лінійність невласних інтегралів) |
|
|
Якщо
невласний інтеграл збігається для
функцій
|
Нехай
![]() ,
,
![]() неперервна майже скрізь на множині
неперервна майже скрізь на множині
![]() та не інтегрована за Ріманом у введених
раніше означеннях. Розглянемо функцію
та не інтегрована за Ріманом у введених
раніше означеннях. Розглянемо функцію
![]() :
:
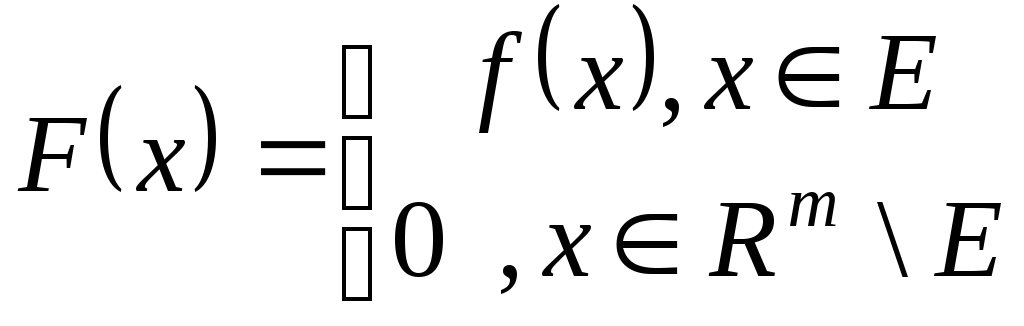 .
Невласний
.
Невласний
![]() кратний
інтеграл
кратний
інтеграл
![]() (13)
назвемо
(13)
назвемо
![]() кратним
невласним
інтегралом
від функції
кратним
невласним
інтегралом
від функції
![]() на множині
на множині
![]() і позначимо його символом
і позначимо його символом
![]() .
.
|
Приклад 1. |
Дослідити на збіжність невласний інтеграл: |
|
|
|
|
|
|
|
|
|
|
|
|
(14) |
|
|
де
|
|
|
|
|
(15) |
|
|
|
|
|
Приклад 2. |
Дослідити
на збіжність невласний інтеграл: |
|
|
|
|
|
|
Аналогічно
Прикладу 1
|
-
збіжний, якщо -розбіжний,
якщо
|
|
|
Ознака 1. |
(Загальна ознака порівняння) |
|
|
Нехай
|
Доведення
очевидно (послідовність
![]() обмежена).
обмежена).
|
Ознака 2. |
(Ознака збіжності на нескінченності) |
|
|
Якщо
функція
|
|
Ознака 3. |
(Ознака збіжності в нулі) |
|
|
Якщо
функція
|
|
Теорема 5. |
(Заміна змінної в невласному інтегралі) |
|
|
|
Нехай
|
|
|
|
|
(16) |
|
|
існує, то наступний інтеграл . |
|
|
|
|
(17) |
|
|
також існує і вони рівні між собою |
|
Доведення.
Спочатку припустимо, що
![]() .
У цьому випадку достатньо дослідити
поведінку інтегралів (16)
та (17)
на одній припустимій послідовності
множин. Візьмемо якусь припустиму
послідовність множин (
.
У цьому випадку достатньо дослідити
поведінку інтегралів (16)
та (17)
на одній припустимій послідовності
множин. Візьмемо якусь припустиму
послідовність множин (![]() ),
яка складається з об’єднання скінченої
кількості
),
яка складається з об’єднання скінченої
кількості
![]() вимірних
брусів. Нехай
вимірних
брусів. Нехай
![]() і покажемо, що послідовність (
і покажемо, що послідовність (![]() )
– припустима.
)
– припустима.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
У
кожному околі, який не перетинається з
![]() функція
функція
![]() обмежена тобто усі особливі точки цієї
функції належать цієї множині
обмежена тобто усі особливі точки цієї
функції належать цієї множині
![]() .
.
![]() - образ при регулярному відображенні
відкритої множини є відкритою множиною.
Межа множини
- образ при регулярному відображенні
відкритої множини є відкритою множиною.
Межа множини
![]() є прообразом межі
є прообразом межі
![]() .
Покажемо, що її міра є 0. Розглянемо
функцію:
.
Покажемо, що її міра є 0. Розглянемо
функцію:
 ,
,
![]() вона є неперервною, крім того
вона є неперервною, крім того
![]() - межа множини
- межа множини
![]() є ком пакт
є ком пакт
![]() з теореми про заміну змінних маємо:
з теореми про заміну змінних маємо:
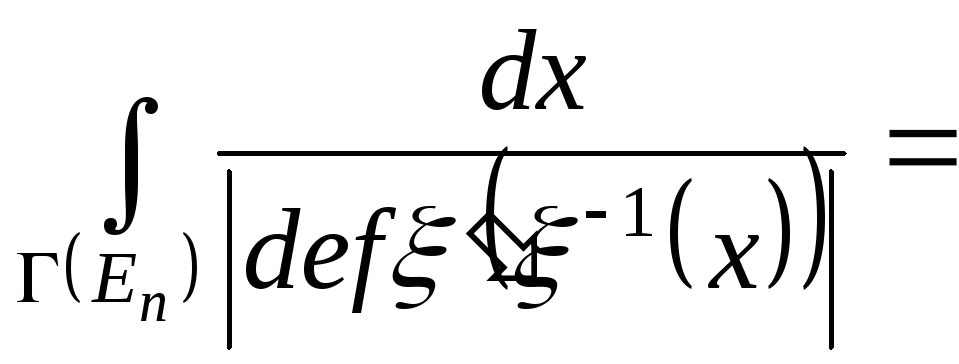
 оскільки
оскільки
![]() - міри 0 (
- міри 0 (![]() -
вимірні за Жорданом ), то міра
-
вимірні за Жорданом ), то міра
![]() дорівнює нулю (значення дорівнює
інтегралу), отже
дорівнює нулю (значення дорівнює
інтегралу), отже
![]() -
є припустимою і за формулою заміни
змінних ми маємо:
-
є припустимою і за формулою заміни
змінних ми маємо:
![]()
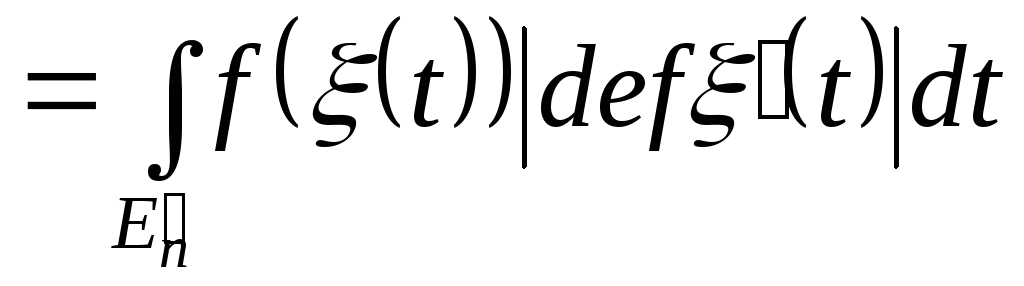 .
Перейдемо до границі при
.
Перейдемо до границі при
![]() і дістанемо бажану рівність.
і дістанемо бажану рівність.

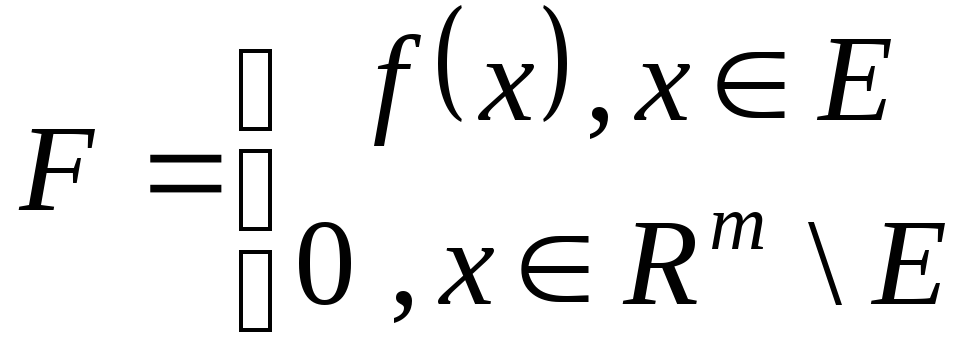 .
Оскільки
.
Оскільки
 ,
,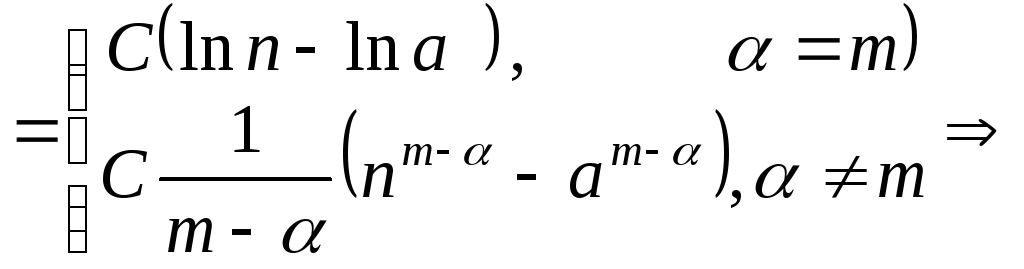 якщо
якщо
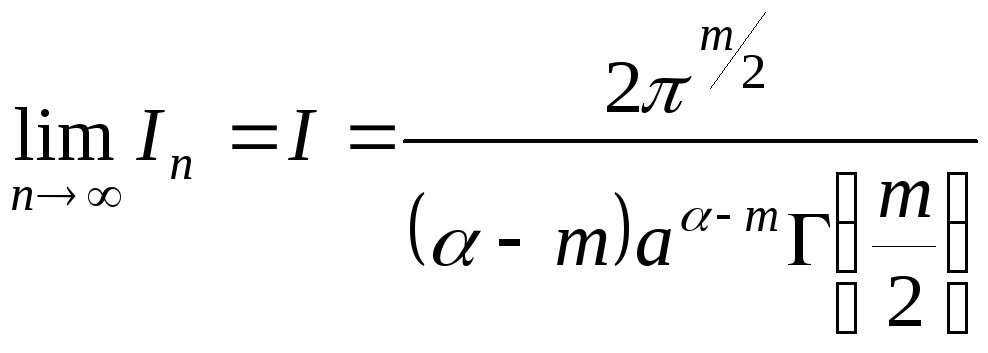 .
.