Задачі.

1. Довести твердження:

а) нехай - міра на алгебрі множин , тоді , мають місце співвідношення:

1) ;

2) ;

3)

4) ;

5) ;

6) ;

7)

;

8) ;

9) для будь-якої скінченої або зліченої сукупності множин ;

10) якщо , то ;

б) адитивна функція є мірою на алгебрі тоді і тільки тоді, коли - -адитивна;

в) нехай - зовнішня міра на -алгебрі множин , тоді мають місце умови:

1) ;

2) ;

3) ;

4) якщо принаймні одна з множин чи вимірна, то в попередньому пункті має місце рівність;

5) якщо до довільної множини додати чи відняти множину міри нуль, то для одержаної множини ;

6) зовнішня міра може бути не адитивною;

г) внутрішня міра в просторі зі скінченною мірою має властивості:

1) невід’ємність ;

2) монотонність;

3) ;

4) злічена-напівадитивність;

5) ;

6) множина - вимірна ;

д) нехай міра визначена на -алгебрі , , тоді:

1) ;

2) , якщо ;

3) множина є кільцем;

4) є -кільцем;

5) якщо для деякої множини і : та , то - вимірна;

е) в просторі монотонними класами є:

1) ;

2) будь-яке -кільце в ;

є) перетин будь-якої кількості монотонних класів є монотонним класом;

ж) нехай - деяка система підмножин основного простору, - відповідно найменша -алгебра та найменший монотонний клас, що містить множину , тоді ;

з) якщо деяка функція, функція множин , що визначена на півкільці півінтервалів дійсної осі, задається таким чином: , тоді - міра на - неспадна та неперервна зліва на функція;

2. Нехай - міра на алгебрі множин , знаючи міри множин (), знайти міри множин:

а) ; б) ;

в) ; г) .

3. Перевірити твердження:

а) якщо міри на алгебрі , то функція , є мірою на ;

б) функція є мірою на алгебрі множин , де:

1) ;

2) , де - фіксована точка простору ;

3) , де - фіксовані точки простору ;

4) , де - фіксована послідовність точок простору ;

5) , де - фіксована послідовність точок простору ;

в) для вказаного простору на -алгебрі задана міра буде -скінченною, де:

1) , ;

2) , ;

3) , ;

4) , задана функція і ;

г) зовнішня міра напівадитивна;

д) якщо зовнішні міри на , то зовнішньою мірою також є функція:

1) ;

2) , ;

е) функція є зовнішньою мірою у розумінні аксіоматичного означення на алгебрі множин , де:

1) , де - фіксована точка простору ;

2) ;

3) , ;

4) , - дорівнює кількості елементів множини і ;

є) для сукупності множин , де такі, що множини не порожні, покладемо , , тоді:

1) - злічено-адитивна на ;

2) існує нескінченно багато продовжень до міри на ;

3) попередній пункт суперечить теоремі про існування та єдиність мінімального продовження міри (теорема 8);

4. Побудувати:

а) для простору на -алгебрі міру таким чином, щоб і ;

б) приклад немонотонної функції множин , що задовольняє умовам невід’ємності, зліченої-напівадитивності, а також ;

в) для тих функції з задачі 3д), що є зовнішніми мірами, клас -вимірних множин;

г) приклад послідовності множин , для якої нерівності в задачі 1д)1) стають строгими (усі чи деякі з них);

д) в просторі , де - система усіх прямокутників , в яких довжина чи ширина дорівнюють одиниці, з функцією (площа прямокутника ) два різних продовження на (переконавшись попередньо, що - -адитивна міра на );

е) приклад невід’ємної функції множин , для якої виконуються умови:

1) визначена на деякому півкільці ;

2) ;

3) - адитивна функція;

4) - не є -адитивною функцією;

є) для простору зовнішню міру, якщо на алгебрі міру задано таким чином:

1) , , , ;

2) , , , ;

3) , , , ;

5. Довести, що:

а) якщо - міра на алгебрі _, - її мінімальне продовження на , тоді:

1) ;

2) ;

3) - вимірна , де і ;

4) - вимірна, якщо : та ;

б) якщо - міра на алгебрі _, - її зовнішня міра, тоді:

1) відношення ~ є відношенням еквівалентності на ;

2) якщо - відповідна фактор-множина, - її елементи, то функція , де , , є метрикою на ;

в) якщо - міра на алгебрі _{, визначимо множину і міру на , тоді:}

_{1) -} -алгебра;

2) - повна міра на _{(цю міру називають поповненням міри );}

_{г) якщо - адитивна функція множин, що визначена на алгебрі , тоді кожна з наступних умов є достатнім для} -адитивності :

1) для будь-якої монотонно зростаючої послідовності множин , для якої ;

2) для будь-якої монотонно спадної послідовності множин , для якої і : ;

3) для будь-якої монотонно спадної послідовності множин , для якої і : ;

д) для алгебри , у якої , виконуються умови:

1) - злічено-адитивна на ;

2) не можливо продовжити до міри на ;

3) це не суперечить теоремі про існування продовження міри (теорема 2);

6. В просторі розглянемо півкільце прямокутників з вигляду . Покладемо на функцію .

а) перевірити, чи буде функція мірою, що визначена на півкільці ;

б) описати явний вигляд лебегівського продовження цієї міри;

в) з’ясувати, чи буде вимірною за Лебегом множина ;

7. Нехай - міра на . Довести, що наступні умови:

а) еквівалентні, якщо - кільце;

б) можуть бути не еквівалентними, якщо - півкільце, де:

(усі множини, що розглядаються вибираються з )

1. злічена напівадитивність: ;

2. напівнеперервність зверху, тобто для монотонно спадної послідовності ;

3. напівнеперервність знизу, тобто для монотонно зростаючої послідовності ;

4. неперервність, тобто для послідовності , що має границю ;

8. Нехай два основних простори, - -алгебри в цих просторах, відображення визначено таким чином, що 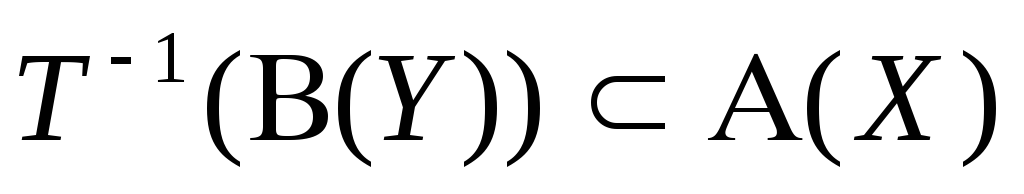, - міра на -алгебрі . Покладемо далі . Довести, що 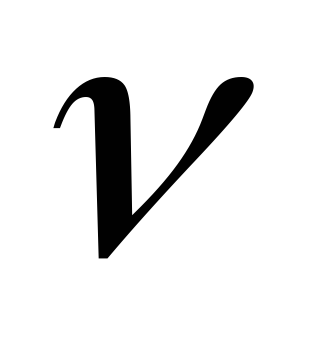- міра на -алгебрі , яку називають образом міри при відображенні .

9. Нехай - довільний простір, довільна послідовність різних точок з 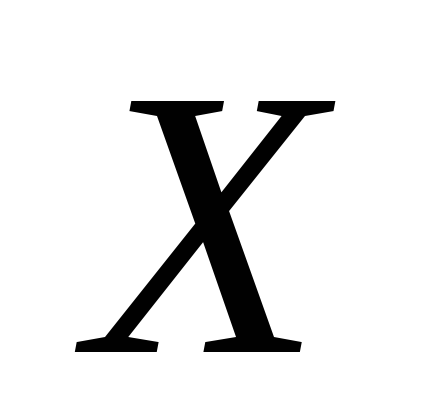, - фіксована послідовність додатних чисел; на -алгебрі визначимо функцію , яку називають дискретною мірою. Довести, що:

а) функція - є мірою на ;

б) якщо ряд - збіжний, то ;

в) якщо ряд - розбіжний, то:

1) ; може приймати й нескінченні значення;

2) міра - -скінчена;

г) функція що дорівнює кількості елементів множини (може приймати нескінчені значення) є дискретною мірою на ;