Lektsii_Rubleva_1 / Гл 11 М_ра Лебега / Пар 11_3 Вим_рн_ множини

9

Глава 11.

МІРА ЛЕБЕГА.

11.3. Вимірні множини.

Нехай як і раніше - основний простір, - деяка алгебра, на якій визначена міра , - зовнішня міра, що визначається за формулою (2.1) . Більшість з наведених далі тверджень справджуються для будь-яких мір, для доведення інших треба звузити клас мір -скінченними.

Множина називається вимірною (вимірною за Каратеодорі), якщо виконується рівність:

. (1)

Сукупність усіх вимірних множин позначимо , а звуження зовнішньої міри на позначимо .

Зауваження.

Оскільки , а тому з напівадитивності зовнішньої міри маємо, що , тобто для доведення вимірності деякої множини треба перевіряти лише зворотню нерівність.

Теорема 1.	(Сукупність вимірних множин)
	Сукупність вимірних множин утворює -алгебру множин, що містить в собі алгебру . Звуження зовнішньої міри на є мірою на (для -скінченої міри).

Доведення проводиться в декілька кроків.

Першій крок. Покажемо, що з умови слідує, що . Запишемо рівність (1) для вимірної множини , замінивши в ньому спочатку на , а далі на . Тоді одержимо:

, (2)

. (3)

Додамо останні дві нерівності, тоді з вимірності зліва одержимо , а тому маємо :

. (4)

В останній рівності, що справджується замінимо на . Перші три доданки правої частини (4) не зміняться при такій заміні, а останній доданок стане дорівнювати: , а тому остаточно одержимо:

. (5)

Порівнюючи (4),(5), одержимо, що :

,

тобто множина - вимірна.

Другий крок. Оскільки при заміні на рівність (1) не змінюється, а тому з вимірності слідує й вимірність . З перших двох пунктів слідує, що - алгебра.

Третій крок. Якщо - диз’юнктна система, то рівність (5) набуває вигляду:

, аналогічно для будь-якої скінченої диз’юнктної системи множин :

. (6)

Четвертий крок. Доведемо, що - -алгебра. Нехай нам задана довільна послідовність множин , яку без обмеження загальності ми можемо вважати диз’юнктною. Для доведення вимірності їх об’єднання достатньо показати, що виконується нерівність :

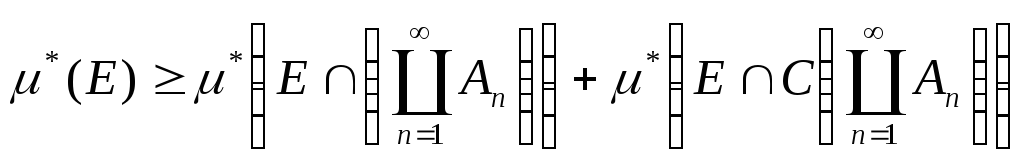. (7)

З того, що - алгебра зрозуміло, що , тому:

,

з формули (6) та з монотонності зовнішньої міри одержимо:

, (8)

(використали очевидне включення , що справджується ), переходимо до границі при , знайдемо:

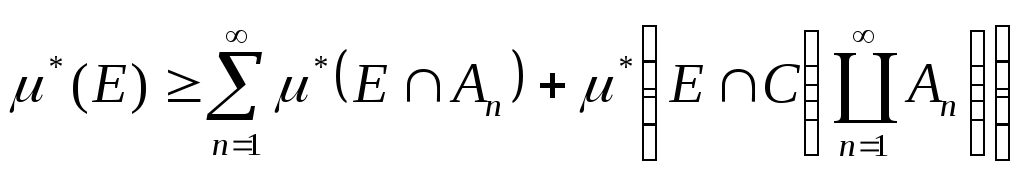. (9)

Із зліченої напівадитивності зовнішньої міри, одержимо

,

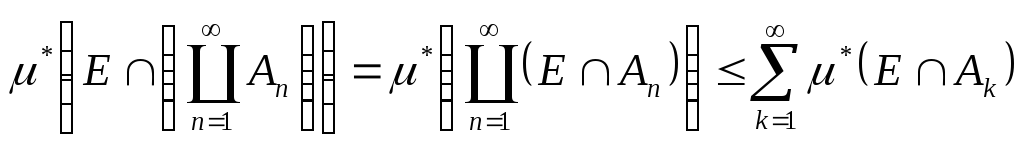додаючи до цієї нерівності (9), одержимо (7), тому , тобто - -алгебра.

П’ятий крок. Доведемо, що на є мірою. Для цього достатньо показати злічену адитивність на . Нехай . Покладемо в (9) , тоді будемо мати , поєднуючи це з зліченою напівадитивністю, одержимо потрібну рівність: .

Шостий крок. Доведемо, що . Для цього достатньо показати, що виконується нерівність :

. (10)

З визначення зовнішньої міри з властивостей інфінума, : , при цьому

. (11)

Кожну з множин подамо у вигляді: , кожна множиня цього об’єднання входить в , тому й

,

тоді нерівність (11) набуває вигляду:

. (12)

Крім того,

, ,

звідки означенню зовнішньої міри, маємо:

, ,

а тому з (12) одержимо:

.

Внаслідок довільності одержуємо те, що треба.

Теорема доведена.

Теорема 2.	(Існування продовження міри)
	Нехай - деяка алгебра, - міра на . Тоді існує -алгебра і міра на , така що її звуження на співпадає з (для -скінченої міри).

Доведення. Все безпосередньо слідує з попередньої теореми. Побудуємо по мірі зовнішню міру і за виберемо -алгебру усіх вимірних (за Каратеодорі) множин, а за - міру . Це й буде шуканим продовженням міри.

Теорема доведена.

Нехай - деяка алгебра, - міра на . Позначимо породжену цією алгеброю -алгебру (мінімальну), побудуємо продовження міри на . Таке продовження називають мінімальним продовженням.

Легко показати, що воно існує. Оскільки , то можемо покласти , як звуження міри на -алгебру . Очевидно, що міра і що це мінімальне продовження міри .

Зауваження.

Якщо - аксіоматично визначена зовнішня міра, то для неї можна визначити аналогічним чином поняття вимірності та вимірної множини. При цьому залишається чинною теорема 1.

Міра , що задана на алгебрі , називається повною, якщо з умов слідує, що . Зрозуміло, з монотонності міри, що при цьому .

Теорема 3.	(Про множини нульової міри)
	Нехай - міра на алгебрі , - її зовнішня міра. Якщо , то множина вимірна й .

Доведення. Для доведення вимірності достатньо показати, що справджується нерівність: , . Оскільки , то з монотонності та невід’ємності міри слідує , аналогічно

, тобто множина вимірна, а далі очевидно, що .

Теорема доведена.

Наслідок.	(Повнота )
	Міра , що одержана як звуження зовнішньої міри на -алгебру вимірних множин є повною.

Теорема 4.	(Неперервність для об’єднання)
	Нехай - міра на -алгебрі , якщо задана монотонно зростаюча послідовність множин , то .

Доведення. Згадавши подання об’єднання через диз’юнктні множини, одержимо:

_,

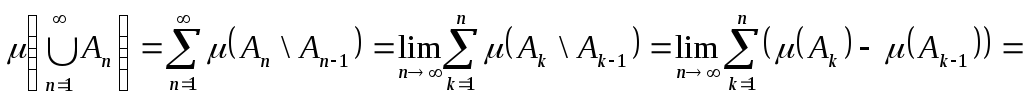
_{з урахуванням того, що .}

_{Теорема доведена.}

Теорема 5.	(Неперервність для перетину)
	Нехай - міра на -алгебрі , якщо задана монотонно спадна послідовність множин , і , то .

Доведення. Без обмежень загальності можемо вважати, що _{, а тому далі за правилами де Моргана легко зведемо задачу до попередньої: 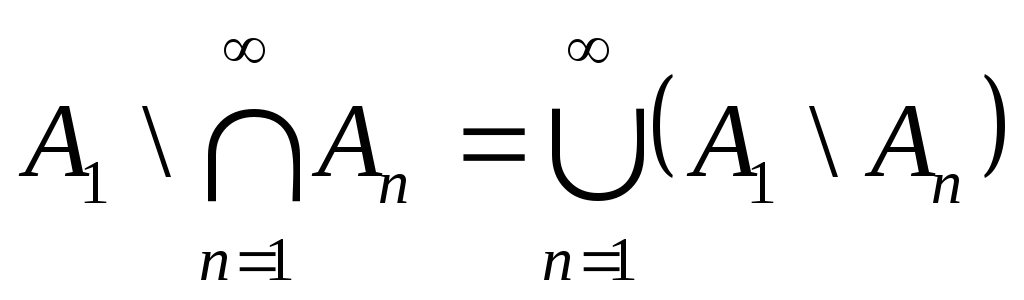, з субтрактивності міри}

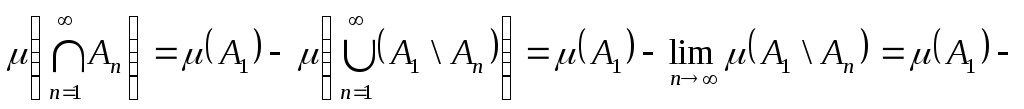
, що й треба довести.

Теорема доведена.

Теорема 6.	(Критерій вимірності)
	Нехай - -скінчена міра на алгебрі множин , - продовження цієї міри на -алгебру вимірних множин . Тоді множина - вимірна () тоді і тільки тоді, коли : .

Доведення. Необхідність. З того, що останню умову можна записати у вигляді . Нехай множина має скінчену міру. З визначення зовнішньої міри : і

. (13)

Оскільки та , то останню нерівність можна переписати у вигляді: .

Запишемо , справа записана монотонно зростаюча послідовність множин, то з теореми 4

, із збіжності ряду можемо вибрати достатньо великим, щоб виконувалась нерівність:

, (14)

тоді покладемо і покажемо, що воно шукане, тобто виконується нерівність 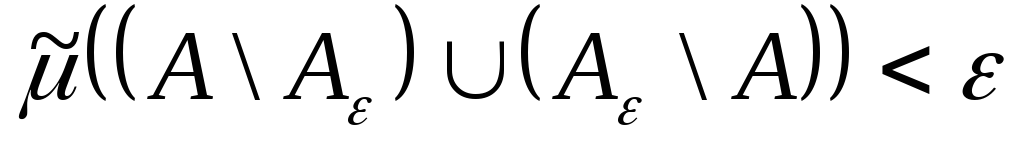, для чого достатньо щоб виконувалися нерівності:

, (15.1)

. (15.2)

Оскільки 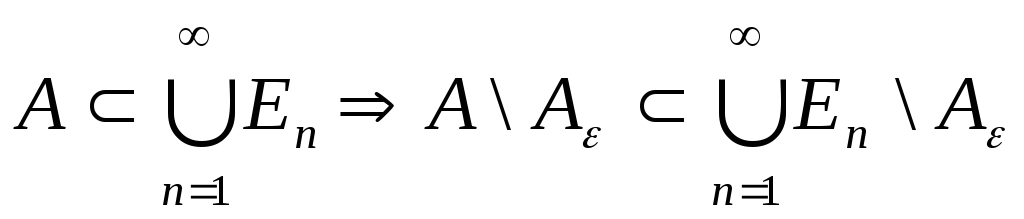, тому з монотонності, субтрактивності міри та з формули (14) маємо:

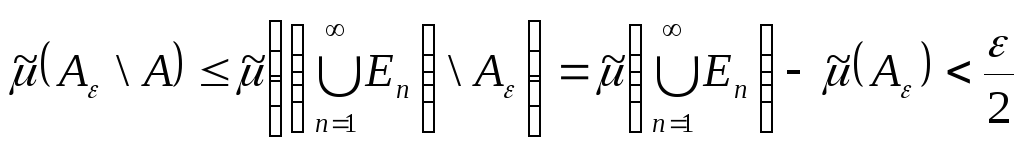, і нерівність (15.1) доведена. Далі, оскільки , то з властивостей міри:

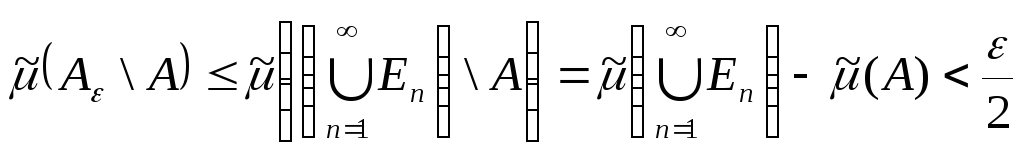, що слідує із співвідношення (13). Таким чином доведена нерівність (15.2), а тому й необхідність доведена.

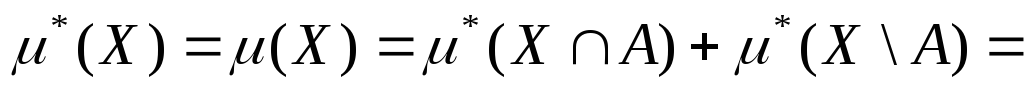
Достатність. Для скінченої міри усе доводиться доволі просто. Якщо - вимірна за Каратеодорі, то , а тому , що еквівалентно вимірності за Лебегом. Інші випадки цієї теореми пропонуємо довести самостійно.

Теорема доведена.

Система підмножин простору називається монотонним класом, якщо разом з будь-якою монотонною послідовністю множин вона містить також її границю .

Лема 1.	(Кільце - монотонний клас)
	Якщо кільце множин є монотонним класом, то - -кільце.

Доведення. Виберемо довільну послідовність множин , побудуємо монотонно зростаючу послідовність множин , з того, що - монотонний клас, слідує, що , що й треба було довести.

Лема доведена.

Теорема 7.	(Про мінімальний монотонний клас)
	Нехай - деяке кільце. Позначимо через породжене кільцем -кільце, а через - мінімальний монотонний клас, що містить . Тоді .

Доведення. Оскільки містить усі можливі злічені об’єднання, а лише об’єднання монотонних послідовностей, то . Якщо ми покажемо, що - кільце множин, то з леми одержимо, що - також -кільце. Тоді оскільки - мінімальне -кільце, що містить , то , з чого й буде слідувати потрібна рівність. Тобто залишається показати, що - кільце множин.