
Lektsii_Rubleva_1 / Гл 06 Ряди / Пар 6-2 Достатн_ ознаки зб_жност_
.docГлава 6
Ряди
6.2. Достатні ознаки збіжності знакосталих рядів
В цьому розділі будемо вважати сі ряди, які ми розглядаємо, є знакосталими, і навіть рядами з додатними членами. Зрозуміло, що для рядів з від’ємними членами мають місце аналогічні властивості.
|
Теорема 0. |
(Критерій збіжності знакосталого ряду) |
|
|
Ряд
|
Доведення.
Монотонно зростаюча послідовність
збіжна в
![]() тоді і тільки тоді, коли вона обмежена.
тоді і тільки тоді, коли вона обмежена.
Теорема доведена.
Нагадаємо,
що дві послідовності дійсних чисел
![]() пов’язані співвідношенням
пов’язані співвідношенням
![]() ,
якщо існує така послідовність
,
якщо існує така послідовність
![]() (обмежена послідовність), для якої
(обмежена послідовність), для якої
![]()
![]() .
В такому разі послідовність
.
В такому разі послідовність
![]() називають мажорантою
для послідовності
називають мажорантою
для послідовності
![]() .
.
|
Теорема 1. |
(Ознака мажорації) |
|
|
Нехай
послідовність
|
Доведення.
Нехай ряд
![]() збіжний, тоді послідовність його
часткових сум
збіжний, тоді послідовність його
часткових сум
![]() монотонно зростає і обмежена. З умови
монотонно зростає і обмежена. З умови
![]() слідує, що
слідує, що
![]() ,
де
,
де
![]() .
Але тоді послідовність
.
Але тоді послідовність
![]() також є обмеженою, крім того вона
монотонно зростає, а тому є збіжною. З
цього і слідує збіжність ряду
також є обмеженою, крім того вона
монотонно зростає, а тому є збіжною. З
цього і слідує збіжність ряду
![]() .
.
Якщо
ряд
![]() розбіжний, то послідовність
розбіжний, то послідовність
![]() необмежена, але тоді і послідовність
необмежена, але тоді і послідовність
![]() також не обмежена, бо вона мажорує
послідовність
також не обмежена, бо вона мажорує
послідовність
![]() .
З цього слідує розбіжність ряду
.
З цього слідує розбіжність ряду
![]() .
.
Теорема доведена.
|
Теорема 2. |
(Ознака порівняння) |
|
|
Якщо
ряд
|
Доведення.
Перепишемо задану нерівність у вигляді:
![]()
![]() ,
а тому виконується така оцінка
,
а тому виконується така оцінка

![]() .
А тому
.
А тому
![]() ,
тобто
,
тобто
![]() ,
і за теоремою 1 ряд
,
і за теоремою 1 ряд
![]() збіжний.
збіжний.
Теорема доведена.
Зі
школи добре відомо, що ряд
![]() ,
тобто сума геометричної прогресії, є
збіжним тоді і тільки тоді, коли
,
тобто сума геометричної прогресії, є
збіжним тоді і тільки тоді, коли
![]() .
Якщо вибрати в останній теоремі в якості
збіжного ряду геометричну прогресію
(тобто
.
Якщо вибрати в останній теоремі в якості
збіжного ряду геометричну прогресію
(тобто
![]() ),
отримаємо такі дві ознаки.
),
отримаємо такі дві ознаки.
|
Теорема 3. |
(Узагальнена радикальна ознака Коші) |
|
|
Для
ряду
|
Доведення.
Нехай
![]() Перепишемо визначення верхньої границі
таким чином:
Перепишемо визначення верхньої границі
таким чином:
![]() .
Виберемо число
.
Виберемо число
![]() таким чином, щоб
таким чином, щоб
![]() .
Тоді існує такий номер
.
Тоді існує такий номер
![]() ,
що
,
що
![]()
![]() .
А тому
.
А тому
![]()
![]() .
Звідси маємо
.
Звідси маємо
![]() ,
а тому
,
а тому
![]() .
З того, що ряд
.
З того, що ряд
![]() - збіжний та з теореми 1 слідує, що й ряд
- збіжний та з теореми 1 слідує, що й ряд
![]() є збіжним.
є збіжним.
Якщо
![]() ,
то виберемо
,
то виберемо
![]() ,
таке що
,
таке що
![]() .
Тоді
.
Тоді
![]() :
:
![]()
![]() .
Але тоді існує така підпослідовність
.
Але тоді існує така підпослідовність
![]() ,
що
,
що
![]()
![]() .
Бо інакше, якщо остання нерівність
виконується тільки для скінченої
кількості членів послідовності, то
позначимо через
.
Бо інакше, якщо остання нерівність
виконується тільки для скінченої
кількості членів послідовності, то
позначимо через
![]() найбільший номер з них, тоді
найбільший номер з них, тоді
![]() ,
що суперечить одержаній нерівності. А
тоді з існування вказаної підпослідовності
слідує, що
,
що суперечить одержаній нерівності. А
тоді з існування вказаної підпослідовності
слідує, що
![]() ,
а це суперечить необхідній умові
збіжності ряду, а тому ряд
,
а це суперечить необхідній умові
збіжності ряду, а тому ряд
![]() - розбіжний.
- розбіжний.
Теорема доведена.
|
Приклад 1. |
Дослідити
на збіжність ряд
|
|
|
Застосуємо одержану ознаку. Знайдемо вказану верхню границю.
|
|
Наслідок. |
(Радикальна ознака Коші) |
|
|
Якщо
для ряду
|
|
Теорема 4. |
(Узагальнена ознака д’Аламбера) |
|
|
Якщо
для ряду
|
Доведення.
Знову виберемо число
![]() таким, щоб виконувались умови:
таким, щоб виконувались умови:
![]() .
Тоді, починаючи з деякого номера
.
Тоді, починаючи з деякого номера
![]() ,
одержимо, що
,
одержимо, що
![]()
![]()
![]()
![]()
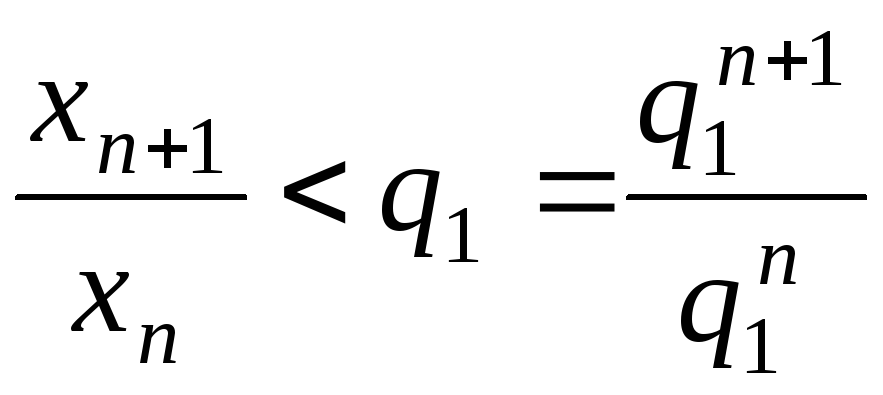 ,
і за теоремою 2 ряд
,
і за теоремою 2 ряд
![]() збіжний.
збіжний.
Теорема доведена.
|
Наслідок. |
(Ознака д’Аламбера) |
|
|
Якщо
для ряду
|
Доведення. Перша частина безпосередньо слідує з теореми, бо якщо існує границя послідовності, то вона співпадає із своєю верхньою границею.
Доведемо
другу частину. За умовою
![]() .
Виберемо число
.
Виберемо число
![]() таким, щоб виконувались умови:
таким, щоб виконувались умови:
![]() .
Тоді, починаючи з деякого номера
.
Тоді, починаючи з деякого номера
![]() ,
одержимо, що
,
одержимо, що
![]()
![]()
![]()
![]()
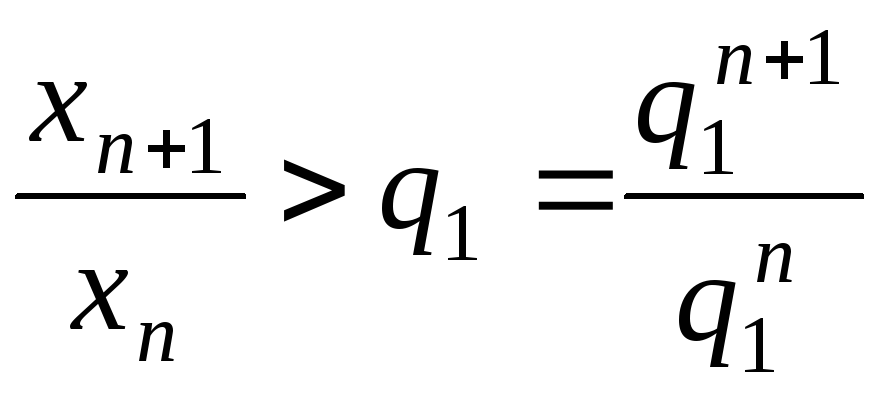 ,
і за теоремою 2 ряд
,
і за теоремою 2 ряд
![]() розбіжний.
розбіжний.
Наслідок доведено.
|
Приклад 2. |
Покажемо,
що з умови
|
|
|
Розглянемо
ряд
Якщо
ж розглянути відношення
|
|
Приклад 3. |
Дослідити
на збіжність ряд
|
|
|
Застосуємо ознаку д’Аламбера
|
|
Теорема 5. |
(Про рівнозбіжність рядів) |
|
|
Нехай
послідовність
|
Доведення.
Розглянемо такі позначення для часткових
сум
![]() ,
,
![]() .
.
Якщо
![]() ,
то
,
то
![]()
![]() ,
а тому
,
а тому
![]() . (1)
. (1)
Якщо
![]() ,
то
,
то
![]()
![]() ,
тобто
,
тобто
![]() . (2)
. (2)
Якщо
ряд
![]() збіжний, то послідовність
збіжний, то послідовність
![]() обмежена, а тому обмеженою є також
послідовність
обмежена, а тому обмеженою є також
послідовність
![]() ,
що слідує з нерівності (1),
тоді
й ряд
,
що слідує з нерівності (1),
тоді
й ряд
![]() є збіжним. Якщо ж ряд
є збіжним. Якщо ж ряд
![]() розбіжний, то відповідна послідовність
часткових сум
розбіжний, то відповідна послідовність
часткових сум
![]() необмежена, а тому й послідовність
необмежена, а тому й послідовність
![]() також необмежена, що слідує з нерівності
(2).
А з останнього слідує, що ряд
також необмежена, що слідує з нерівності
(2).
А з останнього слідує, що ряд
![]() - розбіжний. Повністю аналогічно в
зворотному порядку.
- розбіжний. Повністю аналогічно в
зворотному порядку.
Теорема доведена.
|
Наслідок 1. |
(Збіжність степеневого ряду) |
|
|
Степеневий
ряд
|
Доведення.
Якщо
![]() ,
то розбіжність цього ряду слідує з
необхідної умови збіжності ряду, тобто
загальний член ряду не прямує до нуля.
Нехай тепер
,
то розбіжність цього ряду слідує з
необхідної умови збіжності ряду, тобто
загальний член ряду не прямує до нуля.
Нехай тепер
![]() ,
використаємо теорему, розглянемо ряд
,
використаємо теорему, розглянемо ряд
![]() ,
а це є геометрична прогресія із знаменником
,
а це є геометрична прогресія із знаменником
![]() .
Цей ряд збіжний при
.
Цей ряд збіжний при
![]() ,
тобто при
,
тобто при
![]() ,
та розбіжний в іншому випадку.
,
та розбіжний в іншому випадку.
Наслідок доведено.
|
Наслідок 2. |
(Збіжність степенево-логарифмічного ряду) |
|
|
Ряд
|
Доведення.
Знову розглянемо рівнозбіжний ряд, про
який йдеться у відповідній теоремі.
![]() ,
а далі залишається скористатися наслідком
1.
,
а далі залишається скористатися наслідком
1.
Наслідок доведено.
|
Теорема 6. |
(Ознака Куммера) |
|
|
Якщо
для ряду
Тоді
ряд
|
Доведення.
Спочатку розглянемо перший випадок,
коли існує
![]() ,
для якого виконуються нерівності:
,
для якого виконуються нерівності:
![]() .
Тоді можемо записати:
.
Тоді можемо записати:
![]() .
Записуючи ці нерівності послідовно для
.
Записуючи ці нерівності послідовно для
![]() ,
одержимо:
,
одержимо:
![]()
![]()
............................
![]()
Додамо ці нерівності і будемо мати:
![]() ,
і так як
,
і так як
![]() ,
то
,
то
![]() ,
тобто послідовність
,
тобто послідовність
![]() обмежена, а тому і збіжна.
обмежена, а тому і збіжна.
Нехай
тепер
![]() ,
тоді можемо записати це у такому вигляді:
,
тоді можемо записати це у такому вигляді:
![]() .
Продовжуючи це, маємо:
.
Продовжуючи це, маємо:
![]()
![]()
![]() ,
звідки з розбіжності ряду
,
звідки з розбіжності ряду
![]() слідує розбіжність і ряду
слідує розбіжність і ряду
![]() .
.
Ознака доведена.
|
Наслідок. |
(Ознака Куммера в граничній формі) |
|
|
Якщо
для ряду
Тоді
при
|
Доведення.
Якщо
![]() ,
то
,
то
![]() :
:
![]()
![]() ,
а тепер достатньо застосувати ознаку
Куммера. Аналогічно для від’ємного
,
а тепер достатньо застосувати ознаку
Куммера. Аналогічно для від’ємного
![]() .
.
Наслідок доведено.
|
Теорема 7. |
(Ознака Раабе) |
|
|
Якщо
для ряду
|
Доведення.
Застосуємо ознаку Куммера, поклавши
![]() ,
зрозуміло, що при цьому ряд
,
зрозуміло, що при цьому ряд
![]() - розбіжний. Тоді
- розбіжний. Тоді
![]() ,
а далі залишається використати ознаку
Куммера в граничній формі.
,
а далі залишається використати ознаку
Куммера в граничній формі.
Теорема доведена.
|
Теорема 8. |
(Ознака Гаусса) |
|
|
Якщо
для ряду
-збіжний,
якщо
-
розбіжний , якщо
|
Доведення.
Випадок
![]() безпосередньо слідує з ознаки д’Аламбера.
Випадок
безпосередньо слідує з ознаки д’Аламбера.
Випадок
![]() - це наслідок з ознаки Раабе. Залишається
розглянути випадок
- це наслідок з ознаки Раабе. Залишається
розглянути випадок
![]() .
Тобто ми маємо рівність:
.
Тобто ми маємо рівність:
![]() .
Застосуємо ознаку Кум мера, вибравши в
якості послідовності
.
Застосуємо ознаку Кум мера, вибравши в
якості послідовності
![]() ,
як було показано вище, степенево-логарифмічний
ряд
,
як було показано вище, степенево-логарифмічний
ряд
![]() розбіжний. Тоді маємо:
розбіжний. Тоді маємо:
![]()
![]() .
.
Перший
доданок прямує до нуля, а другий до
![]() ,
тому що для логарифму можна скористатися
відомою формулою еквівалентності:
,
тому що для логарифму можна скористатися
відомою формулою еквівалентності:
![]() .
Таким чином
.
Таким чином
![]() ,
і з ознаки Куммера цей ряд розбіжний.
,
і з ознаки Куммера цей ряд розбіжний.
Теорема доведена.
|
Приклад 4. |
Дослідити
на збіжність ряд
|
|
|
Застосуємо ознаку Гаусса.
|

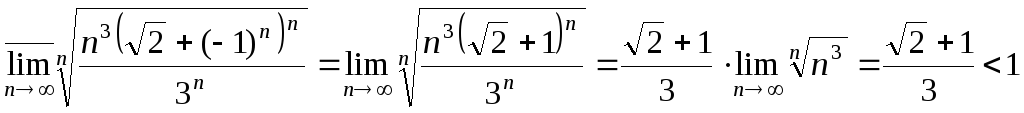 а
тому ряд збіжний.
а
тому ряд збіжний.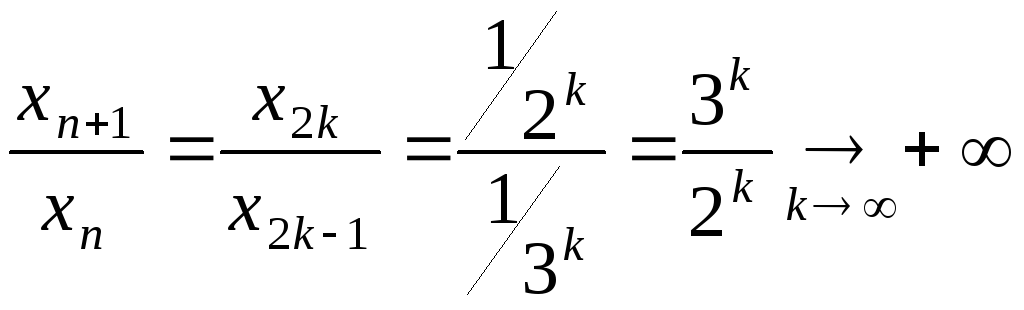 ,
а тому й
,
а тому й
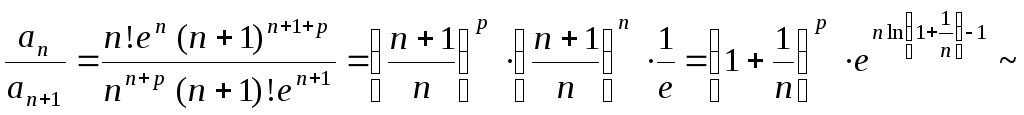
 .
Таким чином
.
Таким чином