
Lektsii_Rubleva / Лекции Рублева-1 / Гл 04 _нтеграл Р_мана / Пар 4-03 _нтеграл Р_мана на дов_льн_й множин_
.doc
Глава 4
Інтеграл Рімана
3. Інтеграл Рімана на довільній множині
Нехай
![]() ,
функція
,
функція
![]() ,
де
,
де
 називається характеристичною
функцією
множини
називається характеристичною
функцією
множини
![]() (ХФ).
(ХФ).
Нехай
![]() ,
,
![]() -
обмежена функція. Якщо
-
обмежена функція. Якщо
![]() ,
то покладемо:
,
то покладемо:
![]() .
.
Нехай
![]() ,
,
![]() - обмежена функція. Продовжимо
- обмежена функція. Продовжимо
![]() на весь
на весь
![]() :
:
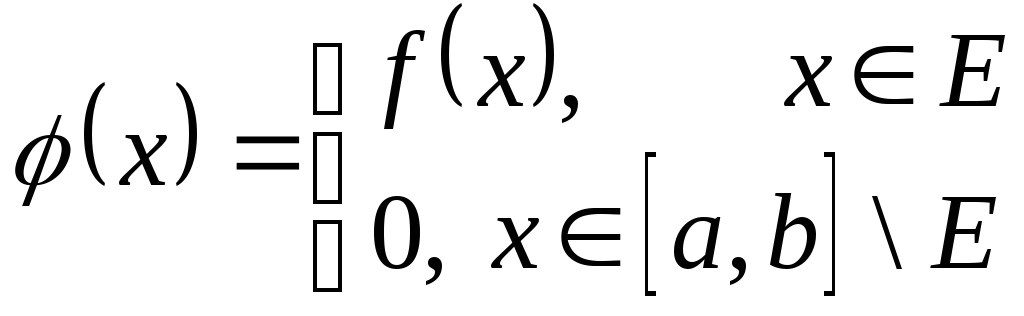 .
Якщо
.
Якщо
![]() ,
то покладемо
,
то покладемо
![]() - цей інтеграл називається інтегралом
Рімана функції
- цей інтеграл називається інтегралом
Рімана функції
![]() по множині
по множині
![]() .
.
|
Властивість. |
(Інтеграл Рімана по одноточковій множині) |
|
|
Для
довільної обмеженої функції
|
Нехай
![]() - впорядкований (частково впорядкований)
простір,
- впорядкований (частково впорядкований)
простір,
![]() - деяка множина з
- деяка множина з
![]() .
Межею
.
Межею
![]() називається множина таких точок, кожна
з яких є точкою дотикання як
називається множина таких точок, кожна
з яких є точкою дотикання як
![]() ,
так і
,
так і
![]() .
Точки множини
.
Точки множини
![]() називаються межовими,
або точками
на межі.
називаються межовими,
або точками
на межі.
|
Приклад 1. |
Знайти
межові точки множин:
|
|
Теорема 1. |
(Інтегрованість ХФ) |
|
|
Нехай
|
Доведення
теореми.
![]() ,
якщо інтеграл справа існує. Нехай
,
якщо інтеграл справа існує. Нехай
![]() - внутрішня точка
- внутрішня точка
![]()
![]()
![]()
![]()
![]() неперервна в усіх внутрішніх точках
множини
неперервна в усіх внутрішніх точках
множини
![]() .
Якщо
.
Якщо
![]() - внутрішня точка
- внутрішня точка
![]() ,
то аналогічно
,
то аналогічно
![]()
![]()
![]()
![]()
![]() - неперервна. Якщо
- неперервна. Якщо
![]()
![]()
![]()
![]()
![]()
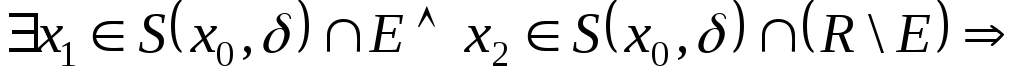
![]()
![]() розривна в точках
розривна в точках
![]() множина точок розриву
множина точок розриву
![]() співпадає з множиною
співпадає з множиною
![]() за теоремою Лебега множина
за теоремою Лебега множина
![]() має лебегова міру нуль.
має лебегова міру нуль.
Теорему доведено.
Обмежена
множина
![]() ,
межа якої має лебегова міру нуль
називається вимірною
за Жорданом,
або жордановою,
а інтеграл
,
межа якої має лебегова міру нуль
називається вимірною
за Жорданом,
або жордановою,
а інтеграл
![]() називається жордановою
мірою
множини
називається жордановою
мірою
множини
![]() (або її довжиною
і назначається
(або її довжиною
і назначається
![]() ).
).
|
Приклад 2. |
Які з множин вимірні за Жорданом. |
|
|
|
|
|
|
|
Теорема 2. |
(Властивості жорданових множин) |
|
|
Нехай
|
|
1) |
|
|
2) |
|
|
3) |
|
Доведення
теореми.
Вимірність за Жорданом очевидна. Нехай
![]() і
і
![]() містить множину
містить множину
![]()
![]()
![]() :
:
![]()
![]()
![]()
![]()
![]() .
.
Якщо
![]()
![]()
![]() і
і
![]()
![]()
![]() .
.
Теорему доведено.
|
Теорема 3. |
(Інтегрованість композиції функцій) |
|
|
Нехай
|
Доведення
теореми.
![]()
![]() міра Лебега точок розриву
міра Лебега точок розриву
![]() дорівнює нулю. Композиція
дорівнює нулю. Композиція
![]() неперервна в кожній точці неперервності
неперервна в кожній точці неперервності
![]() міра Лебега точок розриву
міра Лебега точок розриву
![]() дорівнює нулю
дорівнює нулю
![]()
![]() .
.
|
Приклад 3. |
Якщо
в умовах теореми 3 замінити умову
|
|
|
|
