
Lektsii_Rubleva / Лекции Рублева-1 / Гл 04 _нтеграл Р_мана / Пар 4-02 Теор_я _нтеграла Р_мана
.doc
Глава 4
Інтеграл Рімана
2. Теорія інтеграла Рімана
Нехай
![]() - обмежена функція,
- обмежена функція,
![]() - деяке розбиття сегмента, позначимо
значення
- деяке розбиття сегмента, позначимо
значення
![]() ,
,
![]() ,
,
![]() .
.
Верхньою
та нижньою інтегральними сумами Дарбу,
відповідними розбиттю
![]() для функції
для функції
![]() ,
називаються відповідно суми:
,
називаються відповідно суми:
![]() ,
,
![]() ,
де
,
де
![]() ,
,
![]() .
.
Розбиття
![]() сегмента
сегмента
![]() називається продовженням
розбиття
називається продовженням
розбиття
![]() цього ж сегмента, якщо
цього ж сегмента, якщо
![]() ;
розбиття
;
розбиття
![]() є спільним
для розбиттів
є спільним
для розбиттів
![]() і
і
![]() ,
якщо
,
якщо
![]() .
.
|
Лема 1. |
(Властивості сум Дарбу на продовженні розбиття). |
|
|
|
Якщо
|
|
|
|
|
(1) |
Доведення.
![]()
![]()
![]()
![]() .
Аналогічно для
.
Аналогічно для
![]() .
.
Лему доведено.
|
Лема 2. |
(Зв’язок між верхньою та нижньою інтегральними сумами). |
|
|
|
Для
будь-яких розбиттів
|
(2) |
Доведення.
Нехай
![]() - спільне розбиття, тоді:
- спільне розбиття, тоді:![]() .
.
Лему доведено.
Числа
![]()
![]() ,
,
![]() називаються відповідно верхнім
та
нижнім
інтегралом Дарбу функції
називаються відповідно верхнім
та
нижнім
інтегралом Дарбу функції
![]() на
сегменті
на
сегменті
![]() .
.
(Вони
існують і скінчені внаслідок обмеженості
![]() на
на
![]() ).
).
|
Лема 3. |
(Зв’язок між верхнім та нижнім інтегралами Дарбу). |
|
|
|
Для
будь-якої обмеженої функції
|
|
|
|
|
(3) |
Доведення.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Лему доведено.
Функція
![]() називається інтегрованою
за Дарбу
на
називається інтегрованою
за Дарбу
на
![]() ,
якщо
,
якщо
![]() ,
а спільне значення цих інтегралів
називається інтегралом
Дарбу
і позначається
,
а спільне значення цих інтегралів
називається інтегралом
Дарбу
і позначається
![]() .
Множину всіх інтегрованих за Дарбу
функцій на
.
Множину всіх інтегрованих за Дарбу
функцій на
![]() позначимо через
позначимо через
![]() .
.
|
Теорема 1. |
(Критерій інтегрованості функції). |
|
|
|
Для
того, щоб обмежена функція
|
|
|
|
|
(4) |
Доведення.
Необхідність. Нехай
![]()
![]()
![]() виберемо довільне
виберемо довільне
![]() ,
тоді
,
тоді
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Достатність.
![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Теорему доведено.
|
Теорема 2. |
(Еквівалентність інтегралів Рімана та Дарбу). |
|
|
|
Доведення.
Необхідність.
Нехай
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
Нехай
.
Нехай
![]() містить
містить
![]() точок розбиття
точок розбиття
![]() ,
покладемо
,
покладемо
![]() ,
де
,
де
![]() - коливання функції
- коливання функції
![]() на
на
![]() ,
а тепер розглянемо довільне розбиття
,
а тепер розглянемо довільне розбиття
![]() ,
для якого
,
для якого
![]() ,
а далі позначимо нове розбиття
,
а далі позначимо нове розбиття
![]() .
.
Тепер
оцінимо різницю:
![]() ,
крім того, оскільки інтервал
,
крім того, оскільки інтервал
![]() містить рівно
містить рівно
![]() точок розбиття
точок розбиття
![]()
![]()
![]()
![]()
![]() ,
а т.я.
,
а т.я.
![]()
![]() внаслідок довільності вибору
внаслідок довільності вибору
![]() :
:
![]() .
Аналогічно
.
Аналогічно
![]() .
Але тоді
.
Але тоді
![]()
![]() при
при
![]() ліва та права частини мають границю
ліва та права частини мають границю
![]() ,
з чого слідує, що ту ж саму границю має
і середина.
,
з чого слідує, що ту ж саму границю має
і середина.
Необхідність доведена.
Достатність.
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]() .
Зафіксуємо знайдене розбиття
.
Зафіксуємо знайдене розбиття
![]() .
З властивостей супремуму
.
З властивостей супремуму
![]()
![]() :
:
![]()
![]() якщо додати усі доданки при
якщо додати усі доданки при
![]() ,
справа ми одержимо
,
справа ми одержимо
![]() ,
а зліва
,
а зліва
![]() ,
тобто для множини
,
тобто для множини
![]() при фіксованому
при фіксованому
![]()
![]() є мажорантою та точкою дотику, тому
є мажорантою та точкою дотику, тому
![]() ,
аналогічно
,
аналогічно
![]()
![]()
![]()
![]()
![]() ,
далі одержимо:
,
далі одержимо:
![]() ,
що означає згідно критерію інтегрованості
за Ріманом, що
,
що означає згідно критерію інтегрованості
за Ріманом, що
![]()
![]()
![]() і
і
![]() .
.
Теорема доведена.
|
Приклад 1. |
Обчислити
|
|
|
Складемо
інтегральну суму:
|
Мірою
сегмента
![]() (інтервалу
(інтервалу
![]() ,
півінтервалів
,
півінтервалів
![]() )
називають його довжину:
)
називають його довжину:
![]() .
.
Множина
![]() має лебегову
(жорданову)
міру
нуль,
якщо
має лебегову
(жорданову)
міру
нуль,
якщо
![]() існує злічене покриття
існує злічене покриття
![]() (скінчене покриття
(скінчене покриття
![]() )
інтервалами, сумарна довжина яких не
перевищує
)
інтервалами, сумарна довжина яких не
перевищує
![]() ,
тобто
,
тобто
![]()
![]()
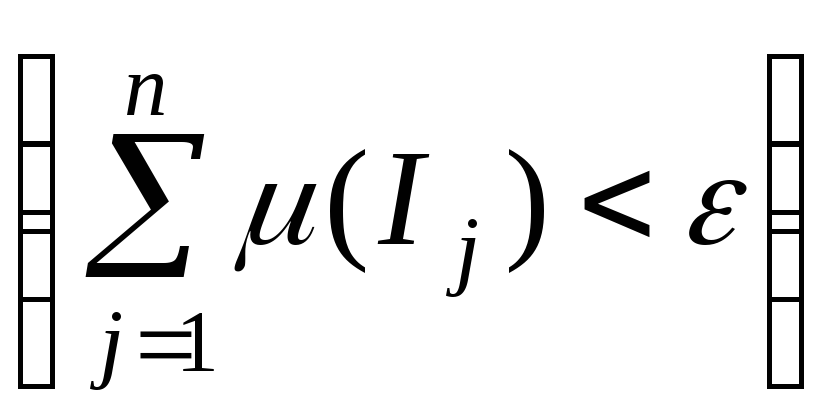 .
.
|
Властивості. |
(Множин лебегової та жорданової міри нуль). |
|
1. |
Якщо
|
|
2. |
Якщо
|
|
3. |
Будь-яка множина жорданової міри нуль є множиною лебегової міри нуль. |
|
4. |
Будь-яка злічена (скінчена) множина точок має лебегову (жорданову) міру нуль. |
|
5. |
Існує більш ніж злічена (більш ніж скінчена) множина, що має лебегова (жорданову) міру нуль. |
Доведення очевидне.
|
Теорема 3. |
(Компакт лебегової міри нуль). |
|
|
Компакт
|
Доведення.
Оскільки компакт має лебегова міру
нуль, то
![]() існує його злічене покриття
існує його злічене покриття
![]() інтервалами, сумарна довжина яких менше
за
інтервалами, сумарна довжина яких менше
за
![]() ,
а тому з леми Гейне-Бореля існує скінчене
підпокриття, а тому його сумарна довжина
також менша за
,
а тому з леми Гейне-Бореля існує скінчене
підпокриття, а тому його сумарна довжина
також менша за
![]() ,
що й означає, що він має жорданову міру
нуль.
,
що й означає, що він має жорданову міру
нуль.
Теорема доведена.
|
Теорема 4. |
(Про замкнену множину). |
|
|
Нехай
|
Доведення.
Покажемо, що доповнення цієї множини
![]() є відкритою множиною. Нагадаємо, що
є відкритою множиною. Нагадаємо, що
![]() ,
а тому
,
а тому
 .
Виберемо довільну точку
.
Виберемо довільну точку
![]() .
Для цього розглянемо два випадки.
.
Для цього розглянемо два випадки.
1)
![]()
![]()
![]() - відкритій множині
- відкритій множині
![]() існує інтервал
існує інтервал
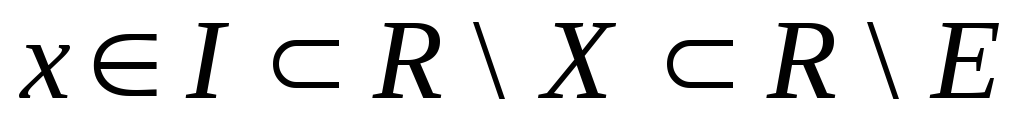
![]()
![]() - внутрішня точка множини
- внутрішня точка множини
![]() .
.
2)
![]() ,
а також
,
а також
![]()
![]()
![]()
![]()
![]() ,
де
,
де
![]()
![]()
![]() :
:
![]() .
Очевидно, що
.
Очевидно, що
![]() :
:
![]() і
і
![]() .
Але тоді
.
Але тоді
![]()
![]() ,
що легко доводиться граничним переходом.
Але тоді довільна точка цього околу
міститься в множині
,
що легко доводиться граничним переходом.
Але тоді довільна точка цього околу
міститься в множині
![]() ,
а тому кожна точка є внутрішньою, з чого
й слідує, що
,
а тому кожна точка є внутрішньою, з чого
й слідує, що
![]() ,
а тому
,
а тому
![]() - відкрита множина, що й треба було
довести.
- відкрита множина, що й треба було
довести.
Таким
чином множина
![]() - відкрита, а тому
- відкрита, а тому
![]() - замкнена.
- замкнена.
Теорема доведена.
|
Теорема 5. |
(Оцінка різниці інтегральних сум). |
|
|
Нехай
|
Доведення.
![]() існує інтервал
існує інтервал
![]() :
:
![]() .
Якщо це не так, то
.
Якщо це не так, то
![]()
![]() ,
а тому існує послідовність інтервалів,
що стягуються до
,
а тому існує послідовність інтервалів,
що стягуються до
![]() ,
тоді граничний перехід показує, що
,
тоді граничний перехід показує, що
![]() ,
а це проти ричить умові. Оскільки
,
а це проти ричить умові. Оскільки
![]() компакт, то з нескінченного покриття
інтервалами, можна виділити скінчене
підпокриття
компакт, то з нескінченного покриття
інтервалами, можна виділити скінчене
підпокриття
![]() .
.
Нехай
![]() таке покриття, що кожний сегмент
таке покриття, що кожний сегмент
![]() цього покриття міститься в деякому з
інтервалів
цього покриття міститься в деякому з
інтервалів
![]() .
Тоді
.
Тоді
![]()
![]() ,
а тому
,
а тому
![]() .
.
Теорема доведена.
|
Теорема 6. |
(Лебега, критерій інтегрованості за Ріманом). |
|
|
Нехай
|
Доведення.
Необхідність.
![]() .
Позначимо множину
.
Позначимо множину
![]() ,
тоді
,
тоді
![]() .
Покажемо, що кожна множина
.
Покажемо, що кожна множина
![]() має лебегову міру нуль. З теореми 4 про
замкнену множину
має лебегову міру нуль. З теореми 4 про
замкнену множину
![]() - замкнена, а тому й вона є компактом. З
того, що
- замкнена, а тому й вона є компактом. З
того, що
![]()
![]()
![]()
![]()
![]() - розбиття
- розбиття
![]() на сегменти
на сегменти
![]() :
:

 .
.