Lektsii_Rubleva / Лекции Рублева-1 / Гл 08 Кратн_ кривол_н_йн_ та поверхнев_ _нтеграли / Пар 8-14 Поверхнев_ _нтеграли

4

Глава 8

Кратні, криволінійні та поверхневі інтеграли

14. Поверхневі інтеграли першого і другого роду

Множина називається простою регулярною поверхнею з класу , якщо на площині існує елементарна множина і таке відображення , що:

1. воно взаємно однозначне (простота поверхні);

2. воно разів неперервно диференційоване на множині (належить до класу );

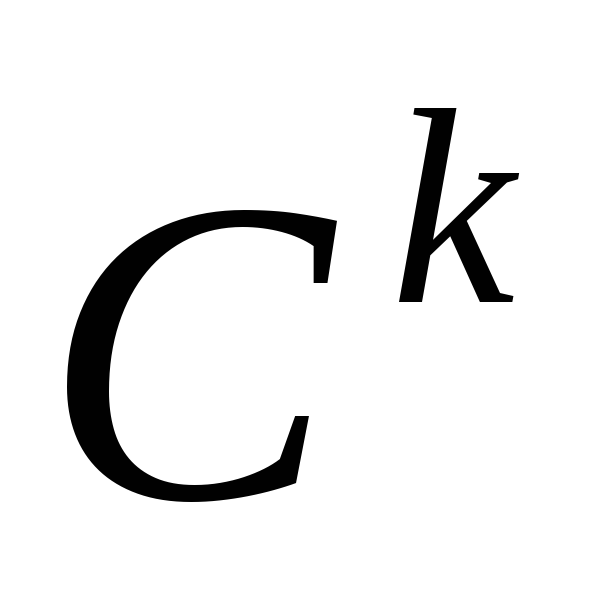3. непаралельне 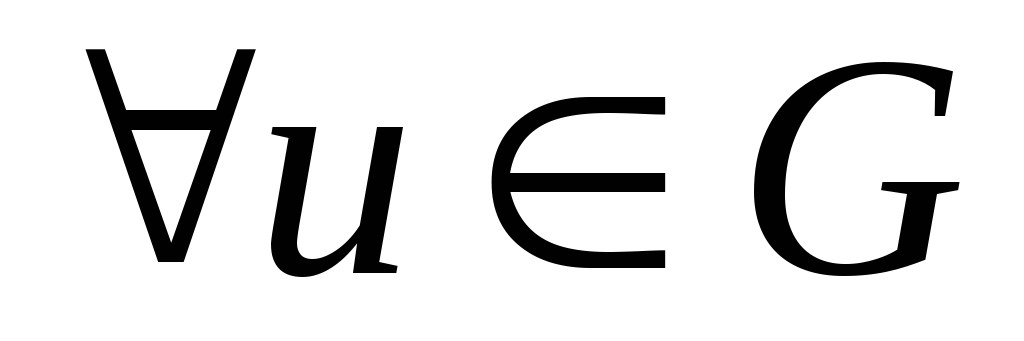, тобто вектори і непаралельні (регулярність).

Якщо , поверхня називається простою гладкою поверхнею в просторі , якщо - називається елементарною.

Кожне відображення , яке має властивості, вказані в означенні, називається параметричним зображенням поверхні , а рівняння , , де радіус-вектор точки – параметричне рівняння поверхні.

В досить малому прямокутному околі точки відображення з точністю до є лінійним:

, . Тому образ прямокутника із сторонами , можна розглядати як фігуру, близьку до паралелограма, побудованого на векторах , , що виходять з точки . Його площа дорівнює: . Звідси природнім буде наступне:

означення: площею елементарної поверхні з параметричним зображенням називається число:

. (1)

Якщо , то (1) можна записати у вигляді:

(2)

де

З теореми про заміну змінних в подвійному інтегралі Рімана випливає незалежність інтеграла від вибору параметризації.

Впровадимо такі позначення:

, , . З рівності , маємо:

(3)

Під коренем бачимо визначник Грамма:

Нехай проста регулярна поверхня, відображення - її параметричне зображення, функція, визначена в точках поверхні. Інтеграл Рімана

, (4) якщо він існує, називається поверхневим інтегралом першого роду від функції по поверхні і позначається символом .

З формули (3) маємо:

(5)

Параметричні зображення , поверхні з класу називаються еквівалентними, якщо існує така бієкція : з класу , що і якобіан .

Клас усіх еквівалентних між собою параметричних зображень поверхні називається її орієнтацією і позначається через . Упорядкована пара , яка складається з поверхні та її орієнтації називається орієнтованою поверхнею.

Нехай - орієнтована поверхня, , задана функція. Якщо існує подвійний інтеграл Рімана

,

(6)

то він називається поверхневим інтегралом другого роду (по й та й змінних) від функції по орієнтованій поверхні і позначається символом

Усі параметричні зображення поверхні , які не належать заданій орієнтації , еквівалентні між собою і утворюють іншу орієнтацію поверхні , яку назвемо протилежною до .

Розглянемо одиничний вектор 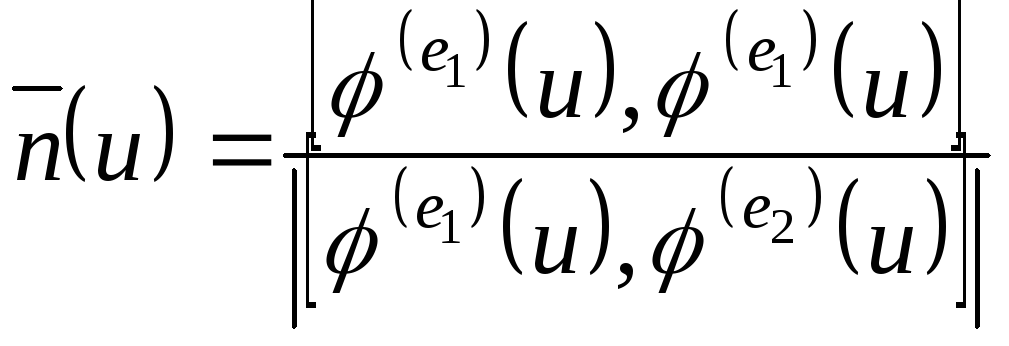, . За властивостями векторного добутку, і ортогонален дотичній площині до поверхні в точці . - одинична нормаль у точці , відповідно до орієнтації . Покажемо, що він не залежить від вибору параметричного зображення . Дійсно, якщо , , то і - еквівалентні, тобто існує бієкція : і . Внаслідок чого маємо:

внаслідок додатності визначника переходу ми маємо, що ці вектори збігаються.

Орієнтація визначається визначенням відповідної їй одиничної нормалі в якій-небудь її точці.

Покладемо:

,

(7)

де орієнтована поверхня, а підсумування ведеться за всіма значеннями .

З того, що , , а також ми можемо привести ліву і праву частини в формулі (7 ) до вигляду:

, (8)

який будемо називати поверхневим інтегралом 2-го роду в стандартній формі. Ну і найчастіше він вживається саме в такому вигляді.

Розглянемо зв’язок між поверхневими інтегралами першого та другого роду. Розглянемо поверхневий інтеграл 2-го роду в стандартній формі при деякій заданій параметризації :

=

;

далі при тій самій параметризації розглянемо такий поверхневий інтеграл 1-го роду:

(9)

з того, що останній множник під інтегралом дорівнює одиниці, ми одержимо рівність:

, (10)

яка й називається формулою зв’язку між поверхневими інтегралами 1-го та 2-го роду.

Залишається розглянути випадок, як спрощується обчислення поверхневого інтегралу 2-го роду у випадку явного визначення поверхні. Тобто треба обчислити ,

при умові що задана така її параметризація:

.

Знайдемо відповідні визначники

, (11)

, (12)

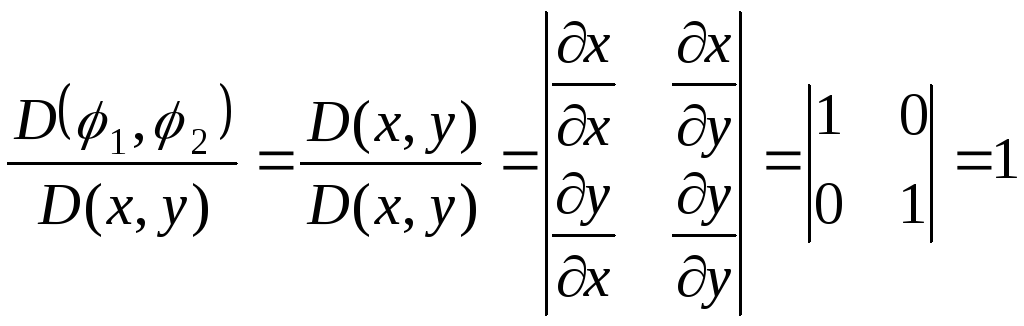, (13)

а тому можемо записати таку формулу для обчислення вказаного поверхневого інтегралу 2-го роду:

,

при цьому знак перед подвійним інтегралом вибирається за таким правилом: вибираємо знак „+”, якщо вектор нормалі до обраної сторони поверхні складає гострий кут з додатнім напрямом осі , і знак - „-” в іншому випадку.