
7_Zakon vsesvitniogo tiazhinnia 7
.pdf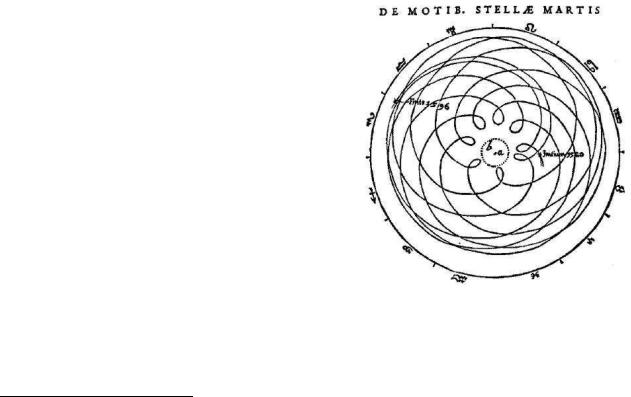
Розділ 7
ЗАКОН ВСЕСВІТНЬОГО ТЯЖІННЯ
7.1. Закони Кеплера та закон всесвітнього тяжіння
Закон всесвітнього тяжіння був уперше сформульований Ісаком Ньютоном у 1687 році в роботі
"Математичні принципи натуральної філософії". Сучасне формулювання цього закону звучить так:
Дві матеріальні точки притягують одна одну вздовж прямої, що їх з’єднує, з силою,
величина якої є прямо пропорційна добутку їх мас і обернено пропорційна квадрату відстані між ними,
F G |
m1m2 |
. |
(7.1) |
|
|||
|
r 2 |
|
|
де m1 та m2 – |
так звані гравітаційні маси частинок, що взаємодіють; r – відстань між |
||
частинками, G – так звана гравітаційна стала.
При формулюванні цього закону Ньютон спирався на сформульовані ним же три закони динаміки та на відомі на той час закони руху планет навколо Сонця, відкриті німецьким астрономом
і математиком Йоганесом Кеплером на підставі аналізу результатів спостережень за рухом планет отриманих
датським астрономом Тихо Браге. Видимий рух планет по небосхилу серед нерухомих одна відносно одної зірок є надзвичайно складним1. На Рис. 7.1 з
оригінальної роботи Кеплера показано траєкторію планети Марс протягом декількох періодів її руху
навколо Сонця. Підсумком його багаторічної праці |
|
були три твердження, що були опубліковані ним у |
|
1609-18 рр. і відомі нині як закони Кеплера: |
Рис. 7.1 |
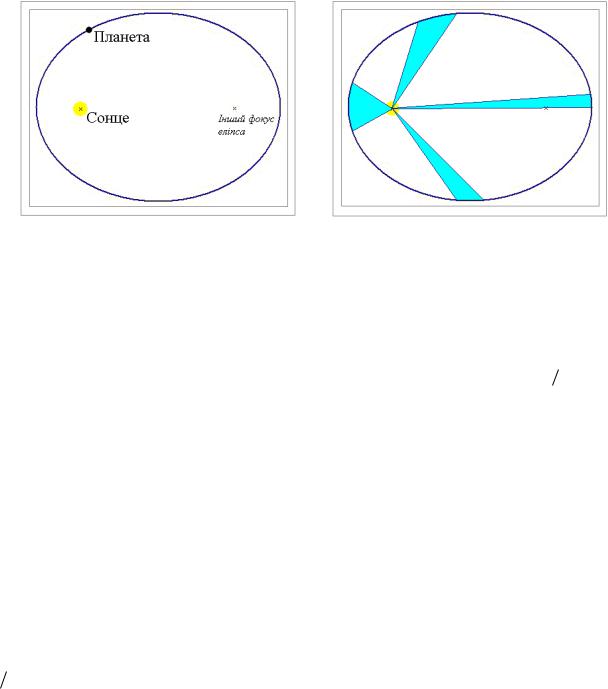
1.Усі планети рухаються по еліпсам, в одному з фокусів яких знаходиться Сонце (Рис. 7.2).
1Цьому факту завдячує саме слово планета: про небесне світило, що безладно рухається по небосхилу греки говорили як про зірку, що блукає.
258
2.Радіус-вектор, що з'єднує Сонце з планетою, за однакові проміжки часу замітає однакові площі (Рис. 7.3).
3.Відношення кубу довжини великої півосі a еліптичні орбіти планети до періоду її обертання T навколо Сонця є величина постійна для всіх планет,
a3 |
const . |
(7.2) |
|
T 2 |
|||
|
|
r
Рис. 7.2 Рис. 7.3
Покажемо як можна із законів динаміки Ньютона та законів Кеплера отримати формулу (7.1).
Оскільки ексцентриситет для більшості планет Сонячної системи (за винятком Плутона та Меркурія)
незначний, будемо вважати їх орбіти коловими. При рівномірному русі по колу прискорення планети
|
|
|
|
2 T , де T – |
має величину a |
2 r , |
де r – радіус-вектор планети відносно центру Сонця, |
||
період обертання планети. |
Отже |
|
||
|
4 2 |
|
|
|
a |
|
r . |
|
(7.3) |
T 2 |
|
|||
Відповідно до другого закону динаміки Ньютона таке прискорення планети виникає внаслідок того, що до неї прикладенаа сила, яка дорівнює добутку її маси m на це прискорення
|
4 2 m |
|
|
F |
|
r . |
(7.4) |
T 2 |
|||
Взявши до уваги третій закон Кеплера, який для колових орбіт ( a r ) набуває вигляду |
|||
r 3 T 2 K , |
де сталу в правій частині, яка дістала назву сталої |
Кеплера, позначено літерою K , |
|
вираз для сили (7.4) можна переписати у вигляді

259
|
K |
4 2 m |
|
||
F |
|
r . |
(7.5) |
||
r 3 |
|||||
|
|
|
|
||
Таким чином, на підставі другого закону Ньютона і третього закону Кеплера можна зробити надзвичайно важливий висновок, що сила, яка прикладена до планети з боку Сонця, є обернено пропорційною квадрату відстані від планети до Сонця. Варто зазначити, що такого кількісного висновку не можна дійти на підставі якихось загальних міркувань: не досить самих законів Кеплера
необхідно використати і другий закон динаміки2. Припускаючи, що всі тіла мають масу, і
спираючись на третій закон Ньютона, можна припустити, що сила притягання між планетою і Сонцем є взаємною, і величина її пропорційна не лише масі планети, рух якої розглядається, а й масі
Сонця M C , яка буде однаковою при розгляді руху будь-якої планети навколо Сонця3. Тоді рівняння
(7.5) можна переписати у вигляді
|
|
k |
4 2 mM |
C |
|
|
||||
|
F |
|
|
|
|
r , |
(7.6) |
|||
|
r 3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
де введено коефіцієнт k через співвідношення K kM C . |
|
|||||||||
Остаточно формули сили, що діє на планету з боку Сонця можна подати у вигляді |
|
|||||||||
|
|
|
|
mM C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
G |
|
|
r |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
F |
|
|
|
|
|
, |
|
(7.7) |
|
|
r 2 |
r |
|
|||||||
який є векторною формою запису закону (7.1).
Цю формулу отримано для руху небесних тіл. Але з давніх давен відоме явище вільного падіння всіх без винятку тіл на поверхню Землі по нормалі до її поверхні. Ґалілей експериментально показав, що при усуненні опору повітря4 всі тіла незалежно від їх складу, форми та інших
властивостей падають по вертикалі з прискоренням g 9,81 м / c2 . З точки зору другого закону Ньютона це прискорення зумовлено силою притягання з боку Землі. Відповідно до третього закону Ньютона тіло з такою ж силою притягує Землю.
2До Ньютона висувалися гіпотези щодо зростання сили тяжіння між небесними тілами при зменшенні відстані між ними, зокрема Кеплер припускав, що ця сила обернено пропорційна просто відстані від планети до Сонця. Сам Ньютон відзначав, що до правильної залежності сили тяжіння від відстані деякі вчені прийшли раніше.
3Сталі Кеплера для систем супутників планет Марса, Юпітера, Сатурна відрізняються від сталої Кеплера для Сонця і
пропорційні масам відповідних планет.
4Ґалілей використовував трубку, з якої було викачане повітря: всередині такої трубки, розміщеної вертикально, різні тіла,
зокрема, важка свинцева кулька і легенька пір’їнка долали відстань від верхнього до нижнього кінця трубки за один і той же час надані самі собі біля верхнього кінця трубки вони надалі рухалися разом.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
260 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
Силу гравітаційного притягання F12 , що діє на частинку з масою |
з боку частинки з масою |
||||||||||||||
m2 можна подати у вигляді |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
m1m2 |
|
|
|
r12 |
|
|
|
|
|
|
|
|
||
F12 |
|
|
|
|
|
|
, |
|
|
|
(7.8) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
r |
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
12 |
|
|
|
|
|
|
|
|
||
де r |
радіус-вектор, |
початок якого співпадає з частинкою маси |
m |
, а кінець з частинкою |
|||||||||||
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
маси m2 , а силу F21 , |
що діє на частинку з масою m2 з боку частинки з масою m1 можна подати у |
||||||||||||||
вигляді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
m1m2 |
|
|
|
r21 |
|
|
|
|
|
|
|
|
||
F21 |
|
|
|
|
|
|
, |
|
(7.9) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
r |
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
21 |
|
|
|
|
|
|
|
|
||
де r21 радіус-вектор, |
початок якого співпадає з частинкою маси m2 , а кінець з частинкою |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
маси m1 . Оскільки r21 |
|
|
r12 |
, то F21 |
F12 , чого й треба очікувати за третім законом Ньютона. |
||||||||||
Ньютон висунув і обґрунтував припущення, що сили, що діють між небесними тілами і сили, що зумовлюють падіння тіл на поверхню Землі, мають спільну природу. Для цього він порівняв величини прискорення Місяця відносно Землі і прискорення вільного падіння тіл поблизу поверхні Землі.
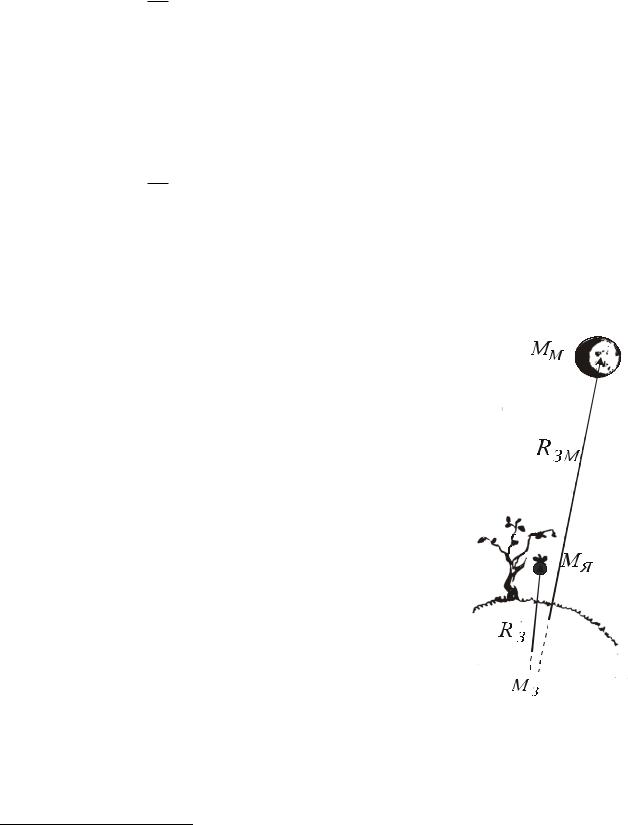
На Рис. 7.4 схематично зображено падіння яблука на поверхню Землі5 та Місяць, що рухається навколо Землі по коловій
орбіті з радіусом RЗМ .
Відповідно до другого закону динаміки Ньютона добуток маси тіла на його прискорення дорівнює силі, що діє на тіло. Отже,
для Місяця можна записати
M |
|
a |
|
G |
M M M З |
, |
(7.10) |
M |
M |
|
|||||
|
|
|
RЗМ2 |
|
|||
|
|
|
|
|
|
||
де |
|
M M та M З маси Місяця та Землі, відповідно, а RЗМ |
|||||
відстані між їх центрами.
Рис. 7.4. Місяць і яблуко в полі тяжіння Землі
5Ньютон згадував, що думка порівняти величини прискорення Місяця відносно Землі і прискорення вільного падіння тіл на поверхню Землі виникла у нього при спостереженні падіння яблук у саду.

261
Якщо припустити, що сила, яка прикладена до яблука з боку Землі й спричинює прискорення його вільного падіння на Землю, має таку саму природу, що й сила, яка прикладена до Місяця з боку Землі й спричинює його рух по орбіті, то для яблука можна записати
m |
|
a |
|
G |
mя M З |
, |
|
(7.11) |
я |
я |
R2 |
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
З |
|
|
|
де |
|
mя маса яблука, а |
RЗ радіус Землі, якому |
з великою точністю дорівнює відстань між |
||||
яблуком і центром Землі.
З рівностей (7.10) та (7.11) випливає просте співвідношення між прискореннями яблука та Місяця
|
a |
я |
|
R |
З |
|
2 |
|
|
|
|
|
|
, |
(7.12) |
||
|
|
|
|
|
||||
|
aM |
|
RЗМ |
|
|
|
||
|
|
|
|
|
||||
яке |
можна |
перевірити на підставі даних спостережень за рухом Місяця та |
за відомою |
|||||
величиною прискорення вільного падіння, з яким падає яблуко aя g 9,81 м c 2 .
|
Період обертання Місяця TM 27,32 доби, а радіус його орбіти |
RЗМ 384 тис. км. Величину |
||||||||||||||||
доцентрової складової прискорення Місяця aM |
можна обчислити за формулою (7.3), |
|
||||||||||||||||
|
a |
|
|
|
4 |
2 |
R |
|
2,72 10 3 м / с2 . |
|
|
|
|
|
|
|||
|
M |
|
|
|
ЗМ |
|
|
|
|
|
|
|||||||
|
|
T 2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
||
|
Тоді відношення прискорень яких набуває яблуко та Місяць внаслідок притягання з боку Землі |
|||||||||||||||||
є |
a |
я |
/ a |
M |
(9,81 м c 2 ) /(2,72 10 3 c 2 ) 3,6 103 602 . |
В |
той |
же |
час |
відношення |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
R |
/ R (384 103 км) /(6,36 103 км) 60,38 . |
Таким |
чином, |
виявляється, |
що |
відношення |
||||||||||||
ЗМ |
|
|
З |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прискорень яблука та Місяця з великою точністю дорівнює квадрату оберненого відношення відстаней від центра Землі до яблука і до Місяця у повній відповідності до формули (7.12), що є вагомим аргументом на користь зробленого припущення про однакову природу сил тяжіння між небесними тілами і силою тяжіння поблизу поверхні Землі. Саме це дає підстави називати закон яжіння (7.1) всесвітнім або універсальним6, оскільки він справедливий для всіх без виключення тіл у Всесвіті.
6Термін універсальний походить від латинського universalis всеосяжний, загальний, який, у свою чергу, походить від латинського universum загальне, Всесвіт.

262
Необхідно підкреслити, що так звані гравітаційні маси m1 та m2 , що фігурують у формулі закону всесвітнього тяжіння (7.1) є мірою гравітаційних властивостей тіл, тобто їх здатності притягуватись одне до одного незалежно від їх інших фізичних властивостей. Вперше силу гравітаційної взаємодії виміряв Кавендіш у 1798 р. у зв’язку з вимірюванням гравітаційної сталої G .
Гравітаційна стала G не може бути визначена з астрономічних спостережень, оскільки для її визначення за формулою (7.1) необхідно знати величину сили, з якою притягуються небесні тіла та гравітаційні маси цих тіл. Кавендішу вдалося безпосередньо виміряти надзвичайно малу силу гравітаційного притягання між двома свинцевими кулями за допомогою винайдених ним крутильних терезів. Той факт, що всі тіла незалежно від будь-яких їхніх властивостей, в тому числі незалежно від величини їх інертної маси, падають біля поверхні Землі з однаковим прискоренням дає можливість припустити, що гравітаційна маса пропорційна інертній. Дійсно, з одного боку на підставі другого закону Ньютона для тіла, що вільно падає біля поверхні Землі, можна записати
mін a G mгрM З ,
RЗ2
а з іншого боку відомо, що для всіх тіл
|
|
(7.13) |
|
|
||
a g . Тоді виявляється, що |
m |
G |
M З |
m |
|
або |
|
гр |
|||||
|
ін |
|
gR2 |
|
||
|
|
|
|
|
||
|
|
|
З |
|
|
|
mін kmгр , тобто інертна маса пропорційна гравітаційній і навпаки. Цей факт є чисто експериментальний. Він дозволяє обрати коефіцієнт пропорційності k 1 ї вважати інертну та гравітаційну маси рівними одна одній, для їх вимірювання використовувати один і той же самий еталон, і встановити для них одну й ту саму одиницю вимірювання, а саме кілограм.
Оскільки одиницею гравітаційної маси є кілограм, а одиниці сили було встановлено раніше на підставі формули другого закону Ньютона, то гравітаційна стала G виявляється розмірною величиною: її розмірність прямо випливає із формули закону всесвітнього тяжіння (7.1). Сучасне значення гравітаційної сталої G (6,6742 0,0010) 10 11 Н м2 кг 2 . Треба сказати, що точність вимірювання G не набагато зросла з часів Кавендіша, оскільки при зовнішній простоті постановки експерименту дуже складно усунути всі фактори, які можуть вносити похибку в обчислену величину
G .

263
7.2. Рух частинки в полі центральної сили, обернено пропорційної квадрату відстані до силового центру
7.2.1 Рух частинки в полі центральної сили
Застосуємо закони збереження моменту імпульсу та енергії до розгляду руху частинки в полі центральної сили.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (r) |
r |
|
||
Оскільки момент центральної сили F |
відносно центра силового поля завжди дорівнює |
|||||||||||
r |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
нулю: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (r) |
|
|
|
|||
|
r |
|
||||||||||
M [r |
F ] [r |
( f (r) |
|
)] |
|
[r |
r ] 0 , |
(7.14) |
||||
r |
r |
|||||||||||
то момент імпульсу частинки в полі центральної сили, визначений відносно центра поля,
зберігається,
|
|
|
L |
[r |
p] const . |
Оскільки центральна сила є консервативна сила, то повна механічна енергія частинки в полі центральної сили також зберігається:
|
m 2 |
|
|
|
|
|
E |
|
U (r) const . |
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
а радіус-вектор частинки |
|
|
Оскільки напрям вектора L є незмінним у просторі, |
r та вектор її |
|||||
імпульсу |
|
|
|
|
|
|
p , а отже і вектор швидкості, перпендикулярні до |
L , траєкторія частинки повністю лежить |
|||||
|
|
|
|
|
|
0 , тобто вона |
в одній площині, перпендикулярній до вектора L . |
Рівняння цієї площини є (L |
r ) |
||||
проходить через центр поля (силовий центр). |
|
|
|
|
||
|
|
|
|
|
|
|
Оберемо напрям осі OZ декартової системи координат вздовж вектора L . Тоді відмінною від |
||||||
|
|
|
Lz L . |
|
|
|
нуля буде лише проекція вектора L на цю вісь, |
Траєкторія частинки при такому виборі |
|||||
системи координат повністю лежить в площині XOY . У координатному записі маємо такі вирази для величини моменту імпульсу та для повної механічної енергії частинки
L m(xy yx)
1 (7.15)
E m(x2 y 2 ) U (r)2
264
Оскільки силове поле центральне, тобто і сила і потенціальна енергія залежать лише від відстані до силового центру, зручно в площині траєкторії ввести полярну систему координат з початком у силовому центрі O.
Якщо полярну вісь полярної системи координат спрямувати вздовж осі OX декартової системи координат, то між x, y та r, існує зв’язок
x r cos
y r sin . |
|
|
|
|
|
(7.16) |
||
Відповідно |
|
|
|
|
|
|
||
x r cos r sin |
|
|
|
|
|
|
||
y r sin r cos . |
|
|
|
|
|
(7.17) |
||
Тоді |
|
|
|
|
|
|
|
|
L m[r cos (r sin r cos ) r sin (r cos r sin )] mr 2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
m[(r cos r sin )2 |
(r sin r cos )2 ] U (r) |
1 |
|
2 |
r 2 |
(7.18) |
E |
|
|
m(r |
2 ) U (r) |
||||
|
|
|
||||||
|
2 |
|
|
2 |
|
|
|
|
і після нескладних алгебраїчних перетворень остаточно |
|
|
|
|
|
|||
L mr 2 |
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
(7.19) |
|
m(r 2 r 2 2 ) U (r) |
|
|
|
|
|
||
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
З виразу для моменту імпульсу (7.19а) випливає, що так звана секторіальна швидкість частинки,
тобто відношення площі d |
1 |
r 2 d , яку «замітає» радіус-вектор частинки |
за елементарний |
||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
проміжок часу dt , до величини цього проміжку є величина стала, |
|
||||||||||||
|
d |
|
d |
( |
1 |
r 2 d ) |
1 |
r 2 |
|
L |
const. |
(7.20) |
|
|
|
|
|
|
|
|
|||||||
|
dt |
|
dt |
2 |
|
2 |
|
2m |
|
||||
Це твердження становить зміст так званого другого закону Кеплера, який встановив його з аналізу спостережень за рухом планети Марс по еліптичній орбіті навколо Сонця в центральному гравітаційному полі останнього, функція потенціальної енергії для якого, як було показано в Розділі 5
(див. формулу (5.36)) є U (r) r .
З виразу для моменту імпульсу також випливає, що знак кутової швидкості, з якою повертається радіус-вектор частинки, є сталим, оскільки

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
265 |
|
|
|
L |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.22) |
|
mr2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
де всі величини в правій частині є додатно визначеними. |
|
|
|
|
|
|
|||||||||||||||||||
За допомогою рівності |
(7.22) можна виключити з виразу для повної енергії частинки (7.19) і |
||||||||||||||||||||||||
подати останню у вигляді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 |
|
|
2 |
|
2 L |
|
2 |
|
1 |
|
2 |
|
L2 |
|
|
1 |
|
2 |
|
|
|
|||
E |
|
|
m r |
|
r |
|
|
|
|
U (r) |
|
mr |
|
|
|
|
U (r) |
|
mr |
|
Uеф |
(r) , |
(7.23) |
||
2 |
|
|
2 |
2 |
|
2mr |
2 |
2 |
|
||||||||||||||||
|
|
|
|
|
mr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де введено так звану ефективну потенціальну енергію |
|
|
|
|
|
|
|||||||||||||||||||
U еф |
(r) |
|
L2 |
U (r) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.24) |
|||||||
2mr 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким чином, вираз для повної енергії частинки в центральному полі має такий самий вигляд як і для повної енергії частинки при одновимірному русі (див. формулу (5.56)), де потенціальну
енергію U (r) замінено на потенціальну енергію Uеф (r) . Отже рух частинки в радіальному
напрямку можна розглядати як одновимірний рух у полі з ефективною потенціальною енергією
Uеф (r) . Швидкість такого руху є
|
dr |
|
2 |
(E U |
|
) |
(7.25) |
|
|
|
еф |
||||
|
dt |
m |
|
|
|||
|
|
|
|
||||
і вона обертається на нуль при умові |
|
||||||
E Uеф (r) |
L2 |
U (r) . |
(7.26) |
|
2mr 2 |
||||
|
|
|
На відміну від випадку одновимірного руху розглянутого в Розділі 5 частинка при цьому не
зупиняється, оскільки завжди існує азимутальна складова швидкості r . Тому радіальний рух
частинки в центральному полі називають квазіодновимірним.
Рівняння траєкторії частинки в полярних координатах можна знайти з рівності (7.22),
виключивши з неї час. Для цього перепишемо її у вигляді |
|
|||
d |
L |
dt , |
(7.27) |
|
mr 2 |
||||
|
|
|
||
підставимо в неї dt , знайдене з рівності (7.25),

266
dt |
|
|
dr |
|
|
|
(7.28) |
|
|
|
|
|
|
||
|
|
|
|
|
|
||
2 |
(E U |
|
) |
||||
|
|
|
|
|
|||
|
|
|
еф |
||||
|
|
m |
|
|
|
||
|
|
|
|
|
|
||
і отримаємо зв’язок між диференціалами d та dr
|
|
|
|
|
|
|
|
L |
|
dr |
|
|
|
|
|
||
d |
|
|
|
|
|
|
mr2 |
|
|
. |
(7.29) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
[E U |
|
|
|
||||||||||
|
|
|
|
|
(r)] |
|
|
||||||||||
|
|
|
|
|
|
еф |
|
|
|||||||||
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для знаходження зв’язку між полярним |
кутом та полярним радіусом r треба |
взяти |
|||||||||||||||
невизначені інтеграли від лівої та правої частин рівняння (7.29) |
|
||||||||||||||||
|
|
|
|
|
|
|
|
L |
|
dr |
|
|
|
|
|
||
|
|
|
|
|
|
|
mr 2 |
|
|
|
0 , |
(7.30) |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
[E U еф (r)] |
|
|
||||||||
|
|
|
|
|
m |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
де через 0 позначено сталу інтегрування. |
|
|
|||||||||||||||
Таким чином, |
|
|
ми отримали (r) , |
тобто рівняння траєкторії у явному вигляді, |
який |
||||||||||||
залежить від конкретного виразу для потенціальної енергії U (r) .
Ясно, що при наявності залежності (r) можна, в принципі, знайти й обернену залежність
r r() .
Як і у випадку істинного одновимірного руху, квазіодновимірний рух можливий лише при таких r , при яких E U еф 0. При цьому він може бути як інфінітним, якщо область можливих значень r обмежена лише знизу, r rmin , або фінітним, якщо rmax r rmin . При цьому характер руху і розміри області, в якій він можливий, визначаються конкретним виглядом потенціальної енергії U (r) і повною механічною енергією частинки. Приклади руху частинки в полі з
потенціальною енергією U (r) при різних значеннях та n подано на Рис.7.5. r n
Необхідно відзначити, що навіть при фінітному русі, коли траєкторія частинки повністю лежить
в кільцевій області rmax r rmin , вона в загальному випадку не є замкненою. Умова замкненості
може бути отримана з таких міркувань. Одновимірний радіальний фінітний рух частинки є
