Симметричный оптимум настройки контуров регулирования

Считается, что замкнутый контур регулирования с единичной отрицательной обратной связью настроен на симметричный оптимум (СО), если он имеет передаточную функцию третьего порядка вида

, (6.7)

где - малая постоянная времени некомпенсируемого апериодического звена;

а_с=3,58 – коэффициент симметричной настройки;

- стандартный коэффициент настройки контура.

Для контура, имеющего стандартную настройку на СО (а_с=8), переходный процесс отработки ступенчатого задающего воздействия представлен на рис.6.4. Он описывается уравнением

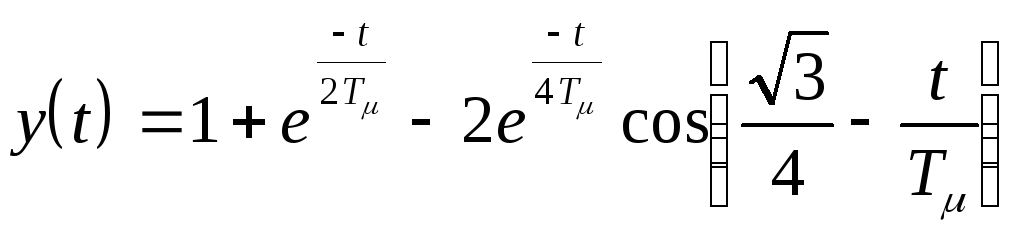(6.8)

и имеет следующие показатели качества: время переходного процесса ; время нарастания ; время первого максимума ; время первого минимума ; перерегулирование %; число колебаний .

Из анализа показателей качества следует, что они в значительной степени отличаются от показателей контура, настроенного на МО.

Б

Рис.6.4. Переходная функция контура регулирования,

настроенного на симметричный оптимум

У– без фильтра на входе,

У_Ф– с фильтром на входе

ольшое перерегулирование, равное=43%, обусловлено влиянием форсирующего звена W(p)=4Tp+1 в числителе передаточной функции (6.7). Перегулирование можно значительно уменьшить, если скомпенсировать числитель передаточной функции, установив на входе управления контура апериодическое звено (фильтр) с постоянной времени

. (6.9)

Тогда передаточная функция по задающему воздействию при стандартной настройке запишется в следующем виде

. (6.10)

Для контура, настроенного на СО с фильтром на входе, переходный процесс отработки ступенчатого задающего воздействия представлен на рис.6.4. Он описывается уравнением

(6.11)

и имеет следующие показатели качества: время переходного процесса ; время нарастания ; время первого максимума ; перерегулирование %; число колебаний .

Следовательно, за счет компенсирующего действия фильтра на входе управления контура достигнуто значительное улучшение динамических показателей.

Разомкнутый контур, настроенный на СО, имеет передаточную функцию

. (6.12)

Рис.6.5. ЛАЧХ и ЛФЧХ разомкнутого контура регулирования, настроенного на симметричный оптимум

1 – стандартная настройка (а_С=8)

2 – настройка на "минимальную колебательность" (а_С=6,4)

Контур, настроенный на СО, содержит в прямой цепи регулирования два интегрирующих звена и поэтому является двукратноинтегрирующей системой. В соответствии с (6.12) на рис.6.5 приведены ЛАЧХ и ЛФЧХ разомкнутого контура, настроенного на СО, где частота среза, - первая частота сопряжения асимптот, - вторая частота

сопряжения. Запас по фазе на частоте среза

=38. ЛАЧХ имеет симметричную форму относительно частоты среза с наклонами асимптот -40дб/дек, -20дб/дек, -40дб/дек. Поэтому такой настройке присвоено название симметричный оптимум. Настройку контура можно несколько улучшить, увеличив в 1,25 раза частоту среза контура, взяв соответственно коэффициент настройки а_с=6,4. В этом случае реализуется настройка на “минимальную колебательность”. Сопрягающие частоты _с1, _с2 при этом должны оставаться неизменными. Применение такой настройки несколько снижает перерегулирование и увеличивает быстродействие, а именно: , 42%. Запас по фазе уменьшается всего на 3 и становится равным _ср=35.

Когда в прямой цепи контура регулирования имеется только одно апериодическое звено с малой постоянной времени, то оно и является звеном с некомпенсируемой постоянной времени.

Если в прямой цепи контура регулирования имеется несколько апериодических звеньев с малыми постоянными времени, то для расчета параметров регулятора эти инерционные звенья необходимо заменить одним эквивалентным апериодическим звеном с постоянной времени Т_е.

, (6.13)

где - эквивалентная некомпенсируемая постоянная времени.