2. Квантор существования.

Определение 7

Пусть А(х) одноместный определённый на М. Высказывание “существует х, что А(х) истинно” обозначается (х) А(х) и считается полученным из А(х) операцией связыванияквантором существования.

(х) А(х) истинно тогда и только тогда, когда существует по крайней мере один элемент из М х₀, для которого А(х) истинен.

Если же для всех элементов из М предикат А(х) ложен, то и (х) А(х) – ложное высказывание.

Пример:

М – множество действительных чисел, Р(x, y) - двуместный предикат,

(x > y). (х)(x > y) – истинно; (х)(x² + y² < 0) – одноместный предикат

Р₁(y), который при любых значениях у принимает значение ложь.

Если М = {a₁, …, a_n} – конечное множество, то выражение (х) Р(х) равносильно следующему высказыванию:P(a₁) P(a₂) …P(a_n).

Определение 8

Если применить квантор существования () по переменнойx₁ к n – местному (n > 1) предикату P (x₁,…, x_n), то получится (n – 1) – местный предикат: Р₁(x₂,…, x_n) = (х)P(x₁,…, x_n), который уже не зависит от переменной x_1, а зависит только от x₂,…, x_n. Причём, при фиксированном наборе х₂⁰, …, х_n⁰ высказывание P₁(х₂⁰, …, х_n⁰) истинно тогда и только тогда, когда одноместный предикат Р(x₁, х₂⁰, …, х_n⁰) истинен по крайней мере при одном х₁ из М.

Уместно говорить о выполнимых формулах на М и на любом поле М..

Примеры:

1) (х)(x² + 1 = y²) одноместный предикат Р(y). Р(1) – истина, т. к. существует 0, что 0 + 1 = 1; Р(2) – ложь, т. к. при любом х x² + 1 4, если хС.

2) (х)(у)(x > y) – истинное высказывание во множестве действительных чисел, но если М – множество натуральные чисел, то

(х)(у)(x > y) - ложно

В этих примерах предикатные символы “=”, “<” истолкованы как

в арифметике.

Теорема 4

Предикат (х₁)P(x₁,…, x_n) = Р₁(x₂,…, x_n),т. е. (n – 1) – местный предикат: Р₁ полученный из Р применением квантора общности тождественно истинен тогда и только тогда, когда тождественно истинен предикат P(x₁,…, x_n).

Теорема 5

(n – 1) – местный предикат, полученный из n – местного предиката P(x₁,…, x_n) операцией связывания квантора существования тождественно ложен тогда и только тогда, когда тождественно ложен предикат P(x₁,…, x_n).

6. Рекурсивные функции, рекурсивные множества. Тезис Черча. Итерация одноместных функций и доказательная база к ней.

Здесь и в дальнейшем будем рассматривать функции от n аргументов f(x₁,…, x_n ), n=0,1,2,…область определения и область значений которых является множество натуральных чисел. Такие функции принято называть арифметическими функциями. Обозначим через К класс арифметических функций, вычислимых в интуитивном смысле. Зададимся целью аксиоматического определения класса К.

1. Определим над арифметическими функциями следующие допустимые операторы:

   1. Оператор суперпозиции. Пусть нам дана одна функция от n переменных f(x₁,…,x_n) и n функций от m переменных g₁(y₁,…,y_m),…,g_n(y₁,…,y_m). Тогда будем говорить, что функция

F(y₁,…y_m)=f(g₁(y₁,…,y_m),…,g_n(y₁,…,y_m)) (1),

получена с помощью суперпозиции функции g₁ вместо переменной x₁, g₂ вместо x₂ и т.д. функцию g_n вместо x_n в функцию f . Например, f(x,y)=x^y, g₁(x)=x, g₂(x)=x+1. Тогда F(x)=x^x+1. В этом определении мы можем допустить, чтобы функции не обязательно содержали одни и те же перемененные. В этом случае достаточно ввести в каждой g_i фиктивные переменные так, чтобы все функции g_i были от одних и тех переменных. Например, если g₁(x) и g₂(y,z), то, введя фиктивно y и z в g₁ и переменную x в g₂, мы получим функции: g(x,y,z)=g₁(x)+0ּy+0ּz, g(x,y,z)=g₂(y,z)+0ּx, которые содержат x,y и z, однако от g₁ и g₂ ничем не отличаются.

2. Оператор примитивной рекурсии.^*)

Рассмотрим две функции: одна от n переменных g(x₁,…,x_n), а другая от (n+2)-переменных h(x₁,…,x_n,y,z). Зададим новую функцию по следующей схеме:

(2).

Убедимся, что схема (2) задает функциональную зависимость по последнему параметру. Действительно, если считать, что первые n переменных (x₁,…,x_n)= зафиксированными, то приy=0 значение f(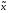,0) совпадает со значением функции g: f(,0)=g(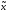),т.е. соответствие однозначное.

При значении y=m+1 значение f однозначно определяется посредством h, используя ее собственное значение при y=m: f(,m+1)=h(,m,f(,m)).

Например, f(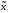,1)=h(,0,f(,0))=h(,0,g());

f(,2)=h(,1,f(,1))=h(,1,h(,0,g()));…

Схема (2) называется схемой примитивной рекурсии, а про функцию f говорят, что она получена из функций g и h по схеме примитивной рекурсии.

Рассмотрим более частные виды схемы (2). При n=0 получим схему

(3),

которая порождает одноместную функцию f с помощью константы a и двуместной функции h(x,y).

Если в (3) функция h одноместная, то получим схему

(4),

которая называется схемой итерации функции h(x) в точке a.

В этом случае все значения функции f(x) зависят только от h: f(1)=h(f(0))=h(a), f(2)=h(f(1))=h(h(a)), f(3)=h(h(h(a))).

Заметим еще, что если существуют алгоритмы (в интуитивном смысле) для вычисления значений функций g()и h(,y,z), то схемы (2), (3) и (4) позволяют вычислить значение функции f для любого набора переменных. То же самое можно сказать и относительно оператора суперпозиции: F(y₁,…y_m)=f(g₁(y₁,…,y_m),…,g_n(y₁,…,y_m)).

Определение 5.1. Функция f называется примитивно рекурсивной, если ее можно получить из начальных функций 0, S(x), I_m⁽ⁿ⁾ конечным числом применений операторов суперпозиции и примитивной рекурсии.

Определение 5.2. Класс примитивно рекурсивных функций К_пр – это наименьший класс арифметических функций, содержащий начальные функции 0, S(x), I_m⁽ⁿ⁾ и замкнутый относительно операторов суперпозиции и примитивной рекурсии.

.

Теорема 5.3. Если функция g(x₁,…,x_n) примитивно рекурсивна, то примитивно рекурсивна и функция, полученная из g с помощью ограниченного оператора суммирования:

Доказательство. Достаточно рассмотреть следующую схему

(10),

которая является схемой примитивной рекурсии и задает с помощью двух примитивно рекурсивных функций g(x₁,…,x_n-1,0) и y+z нужную нам функцию f₆().

Следствие 5.3.1. Функцияявляется примитивно рекурсивной.

Справедливость следствия просматривается из следующего соотношения: .

Следствие 5.3.2. Если примитивно рекурсивны функции g(x₁,…,x_n), k(x₁,…,x_n), l(x₁,…,x_n), то примитивно рекурсивна и функция где суммирование производится отl(x₁,…,x_n) до k(x₁,…,x_n).

Арифметическую функцию f будем считать определенной для набора , если существует некоторый вычислительный процесс, который начавшись с наборазавершается за конечное число шагов и выдаёт результат. Если же процесс продолжается бесконечно, то в этом случае будем считать, чтоf для набора не определена. Еслиf определена для всех наборов, то она называется всюду определенной, в противном случае - частичной.

Определение 7.1. Частичная функция f называется частично рекурсивной, если она может быть получена из начальных функций 0, S(x)=x+1, конечным числом операций, суперпозиции примитивной рекурсии и- операций.

Определение 7.2. Класс частично рекурсивных функций K_rp – это наименьший класс арифметических функций, содержащий начальные функции 0, S(x), и замкнутый относительно суперпозиции, примитивной рекурсии иоперации.

Исследования в области теории рекурсивных функций показали, что любой алгоритмический процесс, встречавшийся до сих пор в математике, может быть сведён к вычислению значений некоторой частично рекурсивной функции. Например, построенная нами в предыдущем параграфе универсальная для класса функцияU(n, x) также является частично рекурсивной. Поэтому в современной математике считается общепринятой следующая гипотеза: класс алгоритмически вычислимых (в интуитивном смысле) функций совпадает с классом всех частично рекурсивных функций, т. е. K=К_чр. Эта гипотеза впервые была высказана А. Чёрчем и поэтому называется тезисом Чёрча и считается основной гипотезой теории вычислимых функций. Эта гипотеза, разумеется не может быть доказана, т. к. в её формулировке содержится такое расплывчатое понятие, как понятие интуитивно вычислимых функций. Однако в её пользу говорит тот факт, что все известные функции из арифметики и теории чисел оказались частично рекурсивными.

Рекурсивные множества

Определение 8.1. Функция f_M(x) называется характеристической функ­цией множества М, если f_M(x)=1 для всех x М и f_M(x)=0 для x М.

Определение 8.2. Множество М называется примитивно рекурсивным, если примитивно рекурсивна его характеристическая функция f_M(x).

Определение 8.3. Множество М называется рекурсивным, если обще­рекурсивна (т.е. всюду определенная ч.р.ф.) его характеристическая функция.

Пример 8.2. Любое конечное множество примитивно рекурсивно. В самом деле, если A={a₁,…,a_k} k – элементное множество, то примитивно рекурсивная функция

f(x)=(|x-a₁|ּ|x-a₂|ּ…ּ|x-a_k|),

которая равна единице, когда xA и нулю, когда x А, является его характеристической функцией.

Теорема 8.1. Объединение и пересечение любого конечного числа (примитивно) рекурсивных множеств, а так же дополнение (примитивно) рекурсивного множество есть множества (примитивно) рекурсивные.

Доказательство. Пусть M₁,M₂,…,M_n-(примитивно) рекурсивные множества и (i=) и их характеристические функции.

Рассмотрим множества

1) - дополнение множестваM₁;

2) - объединение множествM_i;

3) - пересечение множествM_i.

Легко заменить, что для этих множеств характеристическими функциями служат функции , которые также (примитивно) рекурсивные. Теорема доказана.

7. Система счисления с произвольным основанием. Перевод из одной системы счисления в другую. Операции над числами в системах счисления с произвольным основанием.

Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит систем счисления состоит из символов, которые называются цифрами. Например, в десятичной системе счисления числа записываются с помощью десяти всем хорошо известных цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Система счисления - это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления. В позиционных системах счисления значение цифры зависит от ее положения в числе, а в непозиционных - не зависит.

Римская непозиционная система счисления. Самой распространенной из непозиционных систем счисления является римская. В качестве цифр в ней используются: I (1), V (5), X (10), L (50), С (100), D (500), М (1000).

Значение цифры не зависит от ее положения в числе. Например, в числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину - число 10, три числа по 10 в сумме дают 30.

Позиционные системы счисления. Первая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной, то есть в ней использовалось шестьдесят цифр! Интересно, что до сих пор при измерении времени мы используем основание, равное 60 (в 1 минуте содержится 60 секунд, а в 1 часе - 60 минут).

В XIX веке довольно широкое распространение получила двенадцатеричная система счисления. До сих пор мы часто употребляем дюжину (число 12): в сутках две дюжины часов, круг содержит тридцать дюжин градусов и так далее.

В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе.

Наиболее распространенными в настоящее время позиционными системами счисления являются десятичная, двоичная, восьмеричная и шестнадцатеричная. Каждая позиционная система имеет определенный алфавит цифр и основание.

В позиционных системах счисления основание системы равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения одинаковых цифр, стоящих в соседних позициях числа.

Позиционная система счисления определяется целым числом d > 1, называемым основанием системы счисления. Система счисления с основанием d также называется d-ричной

В общем же случае представить произвольное число N в системе счисления с заданным основанием d означает записать его в виде:

N = a_n dⁿ + a_n-1 d^n-1 + … +a₂ d² + a₁ d + a₀

где d - любое целое число, большее единицы. Коэффициенты a₀, a₁, …, a_n называют цифрами в d-ичной системе N. Они могут принимать лишь d значений: 0, или 1, или 2, …, или d -1. В случае d>10 придется придумывать новые символы для цифр.

Совокупность различных цифр, используемых в системе счисления для записи чисел, называется алфавитом системы счисления. Количество этих цифр в d-ичной системе (размерность алфавита) равно основанию системы счисления.

a₀ равно остатку от деления N на d; a₁ равно остатку от деления на d неполного частного, полученного на предыдущем шаге; …………………………………………………………………………………………………… a_n равно остатку от деления на d неполного частного, полученного на предыдущем шаге;

То, что N в d-ичной системе счисления выражается цифрами a_n, a_n-1, …, a₀, записывается так:

N = (a_n a_n-1 …a₁ a₀) _d

Например: 26 700 = (110100001001100) ₂ = (1323300) ₅.

Таким образом, можно сделать выводы: 1) всякое натуральное число, отличное от единицы, может служить основанием позиционной системы счисления; 2) В системе счисления должно быть столько цифр, сколько содержится в основании системы.

Преобразование целых чисел.

Для перевода необходимо исходное число разделить на основание новой системы счисления до получения целого остатка, который является младшим разрядом числа в новой системе счисления (единицы). Полученное частное снова делим на основание системы и так до тех пор, пока частное не станет меньше основания новой системы счисления. Все операции выполняются в исходной системе счисления.

При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.

 Пример: Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

 Ответ: 7510 = 1 001 0112 = 1138 = 4B16.

 При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.

Перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную и обратно.

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

Перевод правильной десятичной дроби в любую другую позиционную систему.

При переводе правильной десятичной дроби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть произведения. Число в новой системе счисления записывается как последовательность полученных целых частей произведения.

Умножение производится до тех поp, пока дробная часть произведения не станет равной нулю. Это значит, что сделан точный перевод. В противном случае перевод осуществляется до заданной точности. Достаточно того количества цифр в результате, которое поместится в ячейку.

Пример: Перевести число 0,35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Ответ: 0,3510 = 0,010112 = 0,2638 = 0,5916.

Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими полиномами. При этом нужно только пользоваться теми таблицами сложения и умножения, которые имеют место при данном основании К системы счисления.

Отметим, что во всех позиционных системах счисления с любым основанием К умножения на числа вида Кm, где т — целое число, сводится просто к перенесению запятой у множимого на т разрядов вправо или влево (в зависимости от знака т), так же как и в десятичной системе.

8. Основные понятия теории кодирования. Оптимальный код Шеннона-Фано.

Задача кодирования информации представляется как некоторое преобразование числовых данных в заданной системе счисления. В частном случае эта операция может быть сведена к группированию символов (представление в виде триад или тетрад) или представлению в виде символов (цифр) позиционной системы счисления. Так как любая позиционная система не несет в себе избыточности информации и все кодовые комбинации являются разрешенными, использовать такие системы для контроля не представляется возможным.

Систематический код — код, содержащий в себе кроме информационных контрольные разряды.

В контрольные разряды записывается некоторая информация об исходном числе. Поэтому можно говорить, что систематический код обладает избыточностью. При этом абсолютная избыточность будет выражаться количеством контрольных разрядов k, а относительная избыточность — отношением k/п , где п = т + k — общее количество разрядов в кодовом слове (т — количество информационных разрядов).

Понятие корректирующей способности кода обычно связывают с возможностью обнаружения и исправления ошибки. Количественно корректирующая способность кода определяется вероятностью обнаружения или исправления ошибки. Если имеем n-разрядный код и вероятность искажения одного символа р, то вероятность того, что искажены k символов, а остальные п-k символов не искажены, по теореме умножения вероятностей будет

w>p^k(1-p)^n-k (8.1)

Число кодовых комбинаций, каждая из которых содержит k искаженных элементов, равна числу сочетаний из п по k:

=(8/2)

Тогда полная вероятность искажения информации

(8-3)

Так как на практике p=10^-3…10^-4, наибольший вес в сумме вероятностей имеет вероятность искажения одного символа. Следовательно, основное внимание нужно обратить на обнаружение и исправление одиночной ошибки.

Корректирующая способность кода связана также с понятием кодового расстояния.

Кодовое расстояние' d(A, В) для кодовых комбинаций А и В определяется как вес третьей кодовой комбинации, которая получается поразрядным сложением исходных комбинаций по модулю 2.

Вес кодовой комбинации V{A) — количество единиц, содержащихся в кодовой комбинации.

Пример 8.1. Найти вес и кодовое расстояние для комбинаций Л = 011011100, B=100111001

Р е ш е и и е Вес для кодовых комбинаций

Коды можно рассматривать и как некоторые геометрические (пространственные) фигуры. Например, триаду можно представить в виде единичного куба, имеющего координаты вершин, которые отвечают двоичным символам (рис. 8.1). В этом случае кодовое расстояние воспринимается как сумма длин ребер между соответствующими вершинами куба (принято, что длина одного ребра равна 1). Оказывается, что любая позиционная система отличается тем свойством, что минимальное кодовое расстояние равно I (рис. 8.2, а).

В теории кодирования [10] показано, что систематический код способен обнаружить ошибки только тогда, когда минимальное кодовое расстояние для нею больше или равно 2t, т. е.

d_min>=2t (8.4)

где t — кратность обнаруживаемых ошибок (в случае одиночных ошибок t = 1 и т. д.).

Это означает, что между соседними разрешенными кодовыми словами должно существовать по крайней мере одно кодовое слово (рис. 8.2, б, в).

В тех случаях, когда необходимо не только обнаружить ошибку, по и исправить ее (т. е. указать место ошибки), минимальное кодовое расстояние должно быть

d_min=2t+1 (8.5)

Существуют коды, в которых невозможно выделить абсолютную избыточность. Пример таких кодов — Д-коды, где количество разрешенных комбинаций меньше количества возможных комбинаций. Неявная избы точность характерна также для кодов типа «Л из и». Примером является код «2 из 5», который часто используется для представления информации. Суть его в том, что в слове из пяти разрядов только два разряда имеют единичное значение.

В общем случае количество n-разрядных слов, имеющих к единичных разрядов, можно оценить по формуле (8.2).

Код Шенона-Фано

Информационную избыточность можно ввести разными путями. Рассмотрим один из путей эффективного кодирования.

В ряде случаев буквы сообщений преобразуются в последовательности двоичных символов. Учитывая статистические свойства источника сообщения, можно минимизировать среднее число двоичных символов, требующихся для выражения одной буквы сообщения, что при отсутствии шума позволит уменьшить время передачи.

Такое эффективное кодирование базируется на основной теореме Шеннона для каналов без шума, в которой доказано, что сообщения, составленные из букв некоторого алфавита, можно закодировать так, что среднее число двоичных символов на букву будет сколь угодно близко к энтропии источника этих сообщений, но не меньше этой величины.

Теорема не указывает конкретного способа кодирования, но из нее следует, что при выборе каждого символа кодовой комбинации необходимо стараться, чтобы он нес максимальную информацию. Следовательно, каждый символ должен принимать значения 0 и 1 по возможности с равными вероятностями и каждый выбор должен быть независим от значений предыдущих символов.

Этот метод требует упорядочения исходного множества символов по не возрастанию их частот. Затем выполняются следующие шаги:

а) список символов делится на две части (назовем их первой и второй частями) так, чтобы суммы частот обеих частей (назовем их Σ1 и Σ2) были точно или примерно равны. В случае, когда точного равенства достичь не удается, разница между суммами должна быть минимальна;

б)  кодовым комбинациям первой части дописывается 1, кодовым комбинациям второй части дописывается 0;

в) анализируют первую часть: если она содержит только один символ, работа с ней заканчивается, – считается, что код для ее символов построен, и выполняется переход к шагу г) для построения кода второй части. Если символов больше одного, переходят к шагу а) и процедура повторяется с первой частью как с самостоятельным упорядоченным списком;

г) анализируют вторую часть: если она содержит только один символ, работа с ней заканчивается и выполняется обращение к оставшемуся списку (шаг д). Если символов больше одного, переходят к шагу а) и процедура повторяется со второй частью как с самостоятельным списком;

д) анализируется оставшийся список: если он пуст – код построен, работа заканчивается. Если нет, – выполняется шаг а).

Пример 1. Даны символы a, b, c, d с частотами fa = 0,5;  fb = 0,25;  fc = 0,125;  fd = 0,125. Построить эффективный код методом Шеннона-Фано.

Сведем исходные данные в таблицу, упорядочив их по невозрастанию частот:

Исходные символы	Частоты символов
a	0,5
b	0,25
c	0,125
d	0,125

Первая линия деления проходит под символом a: соответствующие суммы Σ1 и Σ2 равны между собой и равны 0,5. Тогда формируемым кодовым комбинациям дописывается 1 для верхней  (первой) части и 0 для нижней (второй) части. Поскольку это первый шаг формирования кода, двоичные цифры не дописываются, а только начинают формировать код:

Исходные символы	Частоты символов	Формируемый код
a	0,5	1
b	0,25	0
c	0,125	0
d	0,125	0

В силу того, что верхняя часть списка содержит только один элемент (символ а), работа с ней заканчивается, а эффективный код для этого символа считается сформированным (в таблице, приведенной выше, эта часть списка частот символов выделена заливкой).

Второе деление выполняется под символом b: суммы частот Σ1 и Σ2 вновь равны между собой и равны 0,25. Тогда кодовой комбинации символов верхней части дописывается 1, а нижней части – 0. Таким образом, к полученным на первом шаге фрагментам кода, равным 0, добавляются новые символы:

Исходные символы	Частоты символов	Формируемый код
a	0,5	1
b	0,25	01
c	0,125	00
d	0,125	00

Поскольку верхняя часть нового списка содержит только один символ (b), формирование кода для него закончено (соответствующая строка таблицы вновь выделена заливкой).

Третье деление проходит между символами c и d: к кодовой комбинации символа c приписывается 1, коду символа d приписывается 0:

Исходные символы	Частоты символов	Формируемый код
a	0,5	1
b	0,25	01
c	0,125	001
d	0,125	000

Поскольку обе оставшиеся половины исходного списка содержат по одному элементу, работа со списком в целом заканчивается.

Таким образом, получили коды:

a        -        1,

b        -        01,

c        -        001,

d        -        000.

Определим эффективность построенного кода по формуле:

lср = 0,5*1 + 0,25*01 + 0,125*3 + 0,125*3 = 1,75.

Поскольку при кодировании четырех символов кодом постоянной длины требуется два двоичных разряда, сэкономлено 0,25 двоичного разряда в среднем на один символ.

*

6