Лекция 2(число_е)
.doc
п.2.
Число е
как
предел последовательности
Теорема
2.
Последовательность
–
сходящаяся.
Дано:
последовательность
.
Доказать:
.
Доказательство. 1. Рассмотрим вспомогательную последовательность
, (2)
докажем, что она сходится. Воспользуемся Т. о пределе монотонной последовательности. Заметим, что {уn }– ограниченная, так как по лемме Бернули
,
причём ограничена снизу числом 2.
2. Докажем, что (2) невозрастает, для этого рассмотрим частное:
.
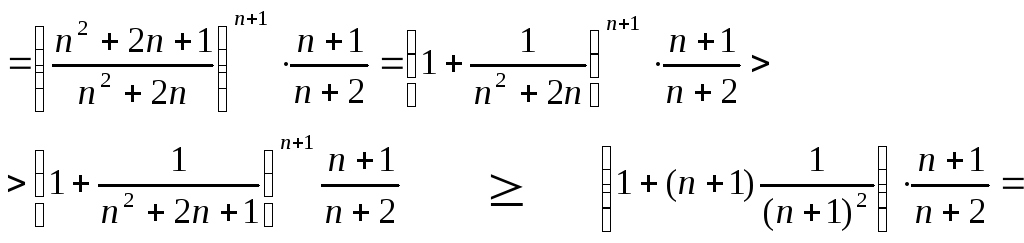
Получили
(2)
– невозрастает.
На основании 1–2 заключаем, что (2) сходится.
Заметим,
что
–
сходится, как частное сходящихся
последовательностей (числитель {
уn
} –сходящаяся последовательность,
знаменатель – сходится, причём
)
.
Замечание
1.
По Л.Эйлеру (швейцарский математик
1707–1783), число, которое является пределом
последовательности
обозначают
e = 2,718281828459045... – иррациональное число, т. обр.
=
e. (3)
Замечание 2. Если число e взяць за основание логарифма, то такой логарифм называют натуральным логарифмом и абазначают ln . Значит, по определению ln х= loge x.
В заключение построим графики функций у= ln х и у=ех (e >1):
