Лабораторная работа № 8

Определение коэффициента внутреннего трения жидкости по методу наблюдения затухания колебаний

1. Цель и задачи работы

Цель работы:

• Ознакомление студентов с методом измерения коэффициента внутреннего трения с помощью крутильного маятника.

Задачи работы:

• Определение постоянной С крутильного маятника.

• Определение коэффициента внутреннего трения жидкости методом затухающих колебаний.

• Определение погрешности измерений.

2. Теоретическая часть

8.2.1. Затухающие колебания. Внутреннее трение

Колебания, амплитуда которых убывает с течением времени, называются затухающими. Закон убывания амплитуд колебаний зависит от характера сил трения, действующих на тело.

Затухающие вращательные колебания можно наблюдать при помощи крутильного маятника. При малых скоростях движения на маятник, вращающийся в жидкости, действуют две силы: сила упругости с моментом , зависящая от свойств нити, на которой он подвешен, и сила трения, момент которого равен, действующая на маятник со стороны жидкости. Вес маятника P и сила растяжения нити T взаимно уравновешиваются.

На основании закона динамики вращательного движения дифференциальное уравнение затухающих колебаний вращающегося тела в жидкости запишется в виде

,

(1)

где J – момент инерции колеблющегося тела, – угловое ускорение затухающих колебаний,k – коэффициент упругости, r – коэффициент сопротивления среды.

Поделив левую и правую части уравнения (1) на момент инерции и введя обозначения ,, получим упрощенное уравнение

.

(2)

Решение уравнения (2) имеет вид

,

где – начальная амплитуда колебаний (максимальное смещение), – коэффициент затухания,  – частота колебания, – начальная фаза колебания.

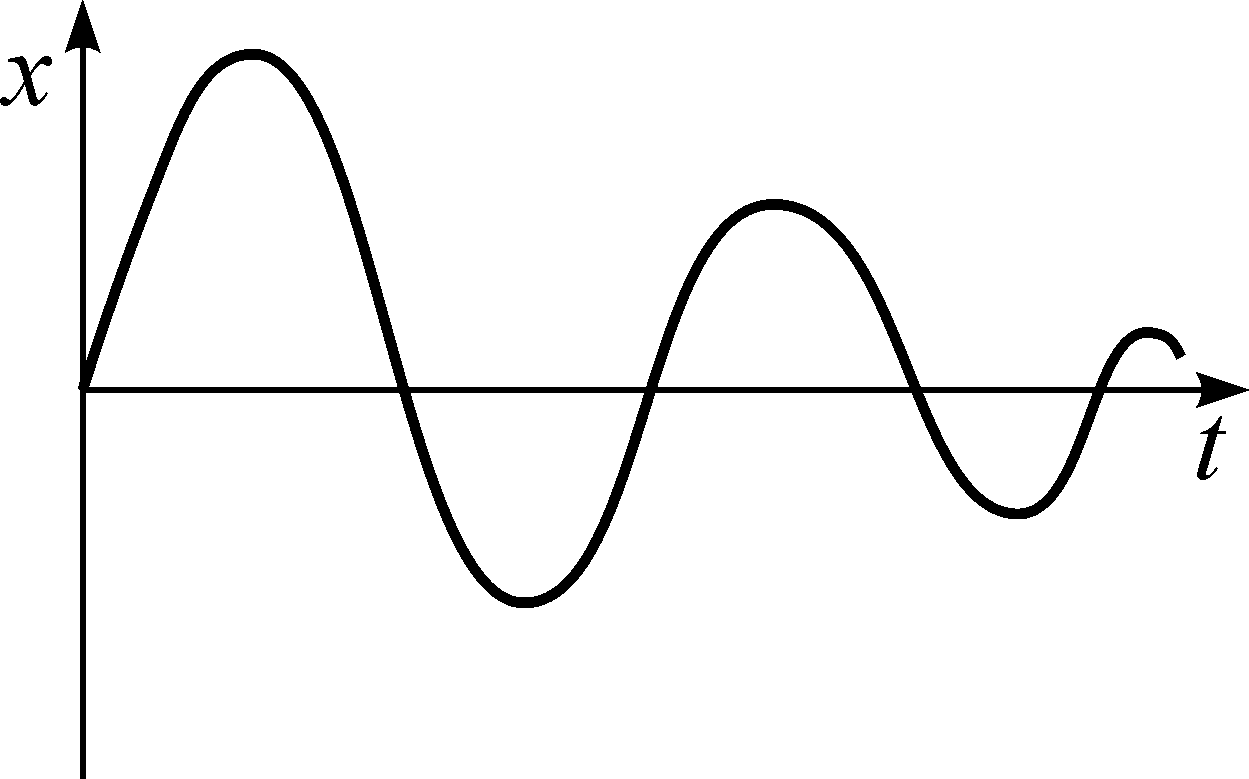
График затухающего колебания представлен на рис. 17.

Рис. 17. График затухающего колебания

Всякое затухающее колебание характеризуется логарифмическим декрементом затухания , который равен логарифму отношения двух амплитуд, отличающихся на период колебаний:

.

В частном случае, при уменьшении амплитуды колебаний в два раза, логарифмический декремент затухания равен , гдеn – число полных колебаний, отсчитанных с момента начала колебаний () до времени, при котором амплитуда колебаний уменьшается в два раза. Зная логарифмический декремент затухания, можно определить коэффициент затухания .

При движении в вязкой среде на тело действует сила внутреннего трения жидкости, определяемая градиентом скорости:

.

Коэффициент внутреннего трения жидкости можно определить путем сравнения затухающих колебаний крутильного маятника в двух жидкостях, вязкость одной из которых известна. В этом случае расчеты ведутся по эмпирической формуле Ньютона:

,

(3)

где  – плотность жидкости при комнатной температуре, T – период колебания в опыте с исследуемой жидкостью,  – логарифмический декремент затухания в исследуемой жидкости, – логарифмический декремент затухания ввоздухе, С – постоянная прибора определяемая выражением

,

(4)

где – вязкость воды,– период колебания в опыте с водой,– плотность воды,– логарифмический декремент затухания в воде.

Плотность и вязкость дистиллированной воды при данной температуре опыта необходимо взять из таблицы 28 (см. приложение 1).