7.2.2. Описание и теория метода

Предлагаемый метод определения показателя адиабаты основан на применении адиабатического и изохорического процессов.

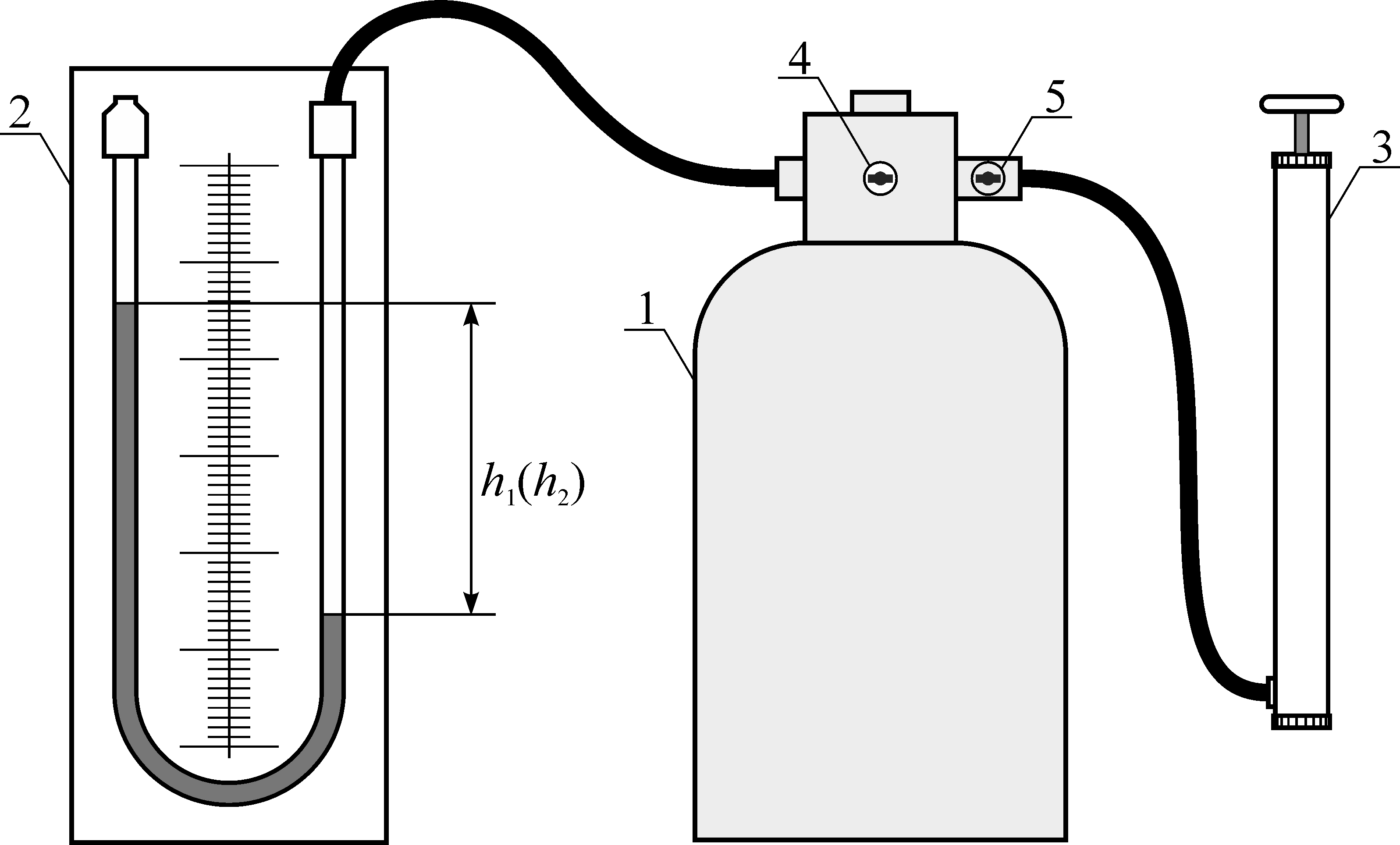
Рис. 16. Экспериментальная установка

Установка состоит из баллона 1, соединенного с манометром 2 и насосом 3 (рис. 16). Посредством крана 4 баллон может быть соединен с атмосферой, и соответственно, первоначальное давление в нем равно атмосферному. Кран 5 служит для закрытия подачи воздуха из насоса. Если с помощью насоса быстро накачать в баллон некоторое количество воздуха и закрыть кран, то давление в баллоне повысится, но если это повышение было произведено достаточно быстро, то манометрический столбик не сразу займет окончательное положение, так как сжатие воздуха было адиабатическим и, следовательно, его температура повысится. Окончательная разность уровней в манометре установится только тогда, когда температура воздуха внутри баллона сравняется, благодаря теплопроводности стенок, с температурой окружающего воздуха.

Обозначим через термодинамическую температуру окружающего воздуха и через– давление газа внутри сосуда, соответствующее показанию манометра. Очевидно, давление, установившееся в сосуде, будет равно

,

(10)

где – приращение давления, происшедшее фактически за счет увеличения массы воздуха в сосуде по сравнению с массой воздуха в начальном состоянии.

Эти два параметра ихарактеризуют состояние газа, которое мы назовем первым состоянием газа.

При быстром открывании крана воздух из сосуда начнет выходить в атмосферу, т.е. расширяться до тех пор, пока давление в сосуде не сравняется с атмосферным. Это расширение происходит достаточно быстро и система не успевает обменяться теплом с окружающей средой. Следовательно, воздух расширяется адиабатически, в результате чего его температура понизится до некоторого значения . Оставшаяся в сосуде массавоздуха будет в состоянии, характеризуемом давлением , температурой и объемом, которое назовем вторым состоянием.

Если после этого снова закрыть кран, то находящийся в сосуде воздух массой при давлении и температуре начнет изохорно нагреваться за счет теплообмена с окружающей средой до тех пор, пока температура внутри и вне сосуда не станет одинаковой. При этом давление указанной массы воздуха увеличится на некоторую величину и станет равным

.

(11)

В итоге мы имеем третье состояние воздуха с параметрами ,,и.

Адиабатический переход воздуха из первого состояния во второе описывается законом Пуассона (9), которое, используя уравнение состояния (2), можно записать в виде

,

(12)

а изохорный переход из второго состояния в третье – законом Гей-Люссака

.

(13)

Принимая во внимание (10) и (11), из (12) и (13) получим

.

Логарифмируя это выражение, имеем:

.

В случае относительно малых изменений давления ипо сравнению с атмосферным, можно воспользоваться соотношением, в итоге получим

,

откуда

.

(14)

Таким образом, при относительно небольших изменениях давления иих измерение дает возможность определить значение.

Установка, схема которой приведена на рис. 16, связана с водяным манометром со шкалой для измерения перепада давления воздуха в баллоне по сравнению с атмосферным. Поэтому изменение давления , заключенного в баллоне воздуха по сравнению с атмосферным давлением, определяется разностью высот уровней воды в коленах манометра

,

где h – разность высот уровней воды в манометре;  – плотность воды; g – ускорение свободного падения.

Поэтому измерениеисводится к измерению соответствующих разностей ивысот уровней воды в коленах манометра, а формула (14) для расчета – к формуле

.

(15)

1. Приборы и принадлежности

• Баллон – 1 шт.

• Манометр – 1 шт.

• Насос – 1 шт.

• Штангенциркуль – 1 шт.

4. Порядок выполнения работы

1. При закрытом кране баллона 4 открыть кран насоса 5 и с помощью насоса накачать в баллон воздух до тех пор, пока разность высот уровней воды в манометре не достигнет 10 – 15 см. Закрыть кран насоса 5.

2. Выждав 2 – 3 минуты, пока температура внутри баллона не станет равной температуре окружающего воздуха, измерить установившуюся разность высот уровней воды в коленах манометра.

3. Поворотом рукоятки крана 4 открыть баллон и в момент, когда уровни воды в коленах манометра сравняются, быстро закрыть кран.

4. Выждать опять 2 – 3 минуты, пока охлажденный при адиабатическом расширении воздух нагреется до прежней (комнатной) температуры, и измерить установившуюся разность уровней .

5. Поворотом крана 4 открыть баллон для установления в нем атмосферного давления, а затем снова закрыть.

6. Повторить опыт 10 раз, меняя каждый раз значение . Результаты эксперимента занести в таблицу 22.

Таблица 22. Коэффициент Пуассона для воздуха

№	h1, мм	h2, мм				, %
1
…
10

5. Обработка результатов измерения

1. По формуле (15) вычислить значение  и записать в таблицу 22.

2. Для определения погрешности измерения необходимо использовать метод наименьших квадратов, т.к. измерения физических величин различны. Зависимость значения уровня высоты отвыражается из (15) линейной зависимостью

,

где .Для начала необходимо вычислить значения величин ,для каждого измерения и записать в таблицу 23, а затем найти среднее значение коэффициентаk по формуле

.

Таблица 23. Оценка погрешности коэффициента Пуассона

№ п/п
1
…
10
	–	–			–

3. Вычислить коэффициент Пуассона по формуле

.

4. Вычислить среднеквадратичную ошибку среднего арифметического, используя данные из таблицы 23 по формуле

.

5. Найти абсолютную погрешность по формуле

,

где коэффициент Стьюдента для надежностии числа измеренийвзять из таблицы 29.

6. Окончательный результат записать в виде

при ,.

6. Контрольные вопросы

1. Что называют удельной (молярной) теплоемкостью вещества?

2. Получите взаимосвязь между удельной и молярной теплоемкостями идеального газа,.

3. Что называют числом степеней свободы молекулы? Чему равно число степеней свободы для одноатомного, двухатомного, трехатомного газа?

4. Пользуясь первым началом термодинамики, получите связь между молярными теплоемкостями при постоянном объеме и при постоянном давлении через число степеней свободы молекулы. Как записывается уравнение Майера?

5. Что такое коэффициент Пуассона? Как объяснить, что его значение для любого газа больше единицы? Чему равен коэффициент Пуассона для воздуха?

6. Какие процессы происходят с воздухом в настоящей работе? Каким законам они подчиняются?

7. Какой процесс называют адиабатическим? Получите уравнение этого процесса для идеального газа, пользуясь первым законом термодинамики и уравнением состояния.

8. Изобразите в координатах адиабатический и изотермический процессы.

9. Что утверждает закон равнораспределения энергии по степеням свободы молекул? Каковы границы его применимости?