03-09-2014_06-10-43 Рабочая тетрадь / Lecture_1s_1k-2konspekt

ЛЕКЦИЯ 2

2.1. Свойства определителей матриц

Вычисление определителя матрицы только по основной теореме не рационально. Таким способом, например, ЭВМ с быстродействием 1 млн. операций в секунду определитель матрицы порядка будет вычислять несколько миллионов лет. С использованием свойств тот же определитель матрицы порядка может быть вычислен за 1 секунду.

Установим ряд свойств, которым обладает произвольный определитель матрицы -го порядка. Покажем справедливость - свойств для .

. При ________________________ матрицы (_______________ ______________________) величина определителя матрицы _____________.

Замечание 1. Свойство устанавливает ____________________ строк и столбцов определителя матрицы. Поэтому любое свойство, которое в дальнейшем будет доказано для строк, окажется справедливым и для _______________.

. ______________________ значение определителя матрицы __________________, сохраняясь по абсолютной величине.

Доказательство. Разложим определитель матрицы по второй строке:

,

поменяем 1 и 3 строки.

Каждое _________________, т.к. является определителем матрицы второго порядка, у которого ________________, следовательно:

.

. Определитель матрицы с двумя одинаковыми строками (столбцами) равен ________.

Доказательство. Допустим, совпадают 1 и 3 строки:

.

Общий множитель всех элементов какой-либо строки _________

_________________ определителя матрицы (т.е. при умножении определителя матрицы на число, _____________ какой-либо ______ строки _______________________________).

Доказательство. Пусть

, .

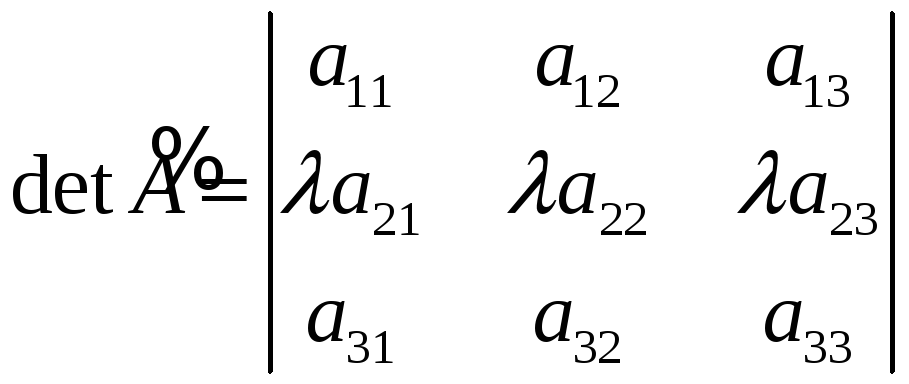Применяя основную теорему, разложим по 2-ой строке, получим:

. Определитель матрицы __________________________________ ______________ (столбцами) равен ______.

Доказательство. Пусть первая и вторая строки пропорциональны. Разложим определитель матрицы по 2-ой строке

. Определитель матрицы, _________________________(столбец), равен ______.

Доказательство. Если все элементы строки равны нулю, то разлагая определитель матрицы по этой строке, получим, что он равен _______.

. Если каждый элемент строки является суммой двух слагаемых, то определитель матрицы равен сумме определителей матриц, в которых элементы этой строки заменены отдельными слагаемыми.

Доказательство. Применяя основную теорему, разложим определитель матрицы по 1-ой строке, получим:

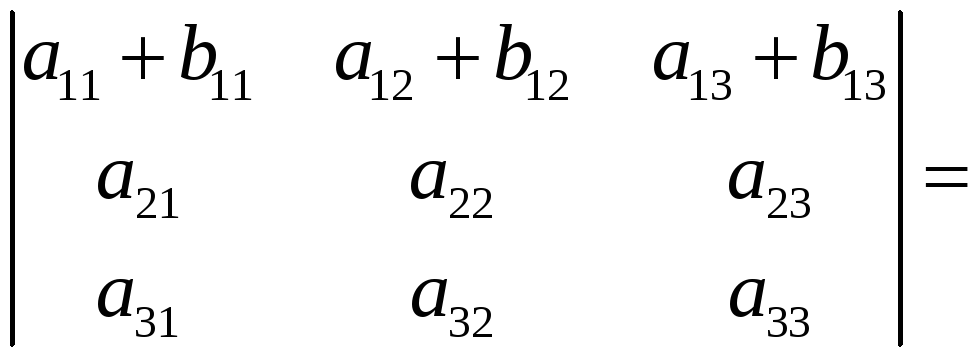
. Значение определителя матрицы _________________, если к элементам какой-либо строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

Доказательство.

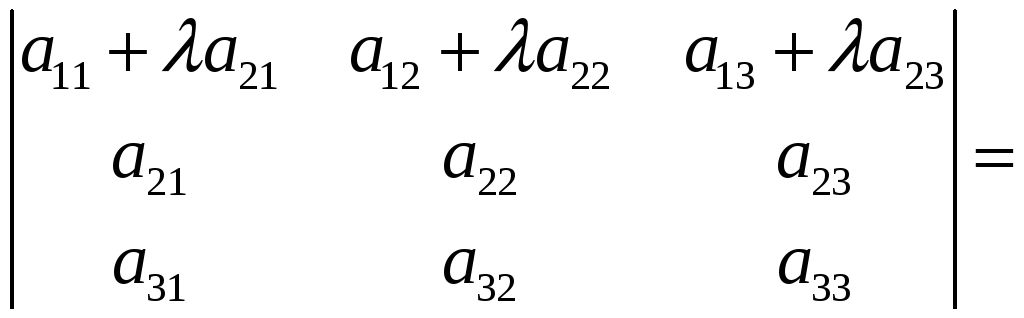
Пример 2.1. Вычислить .

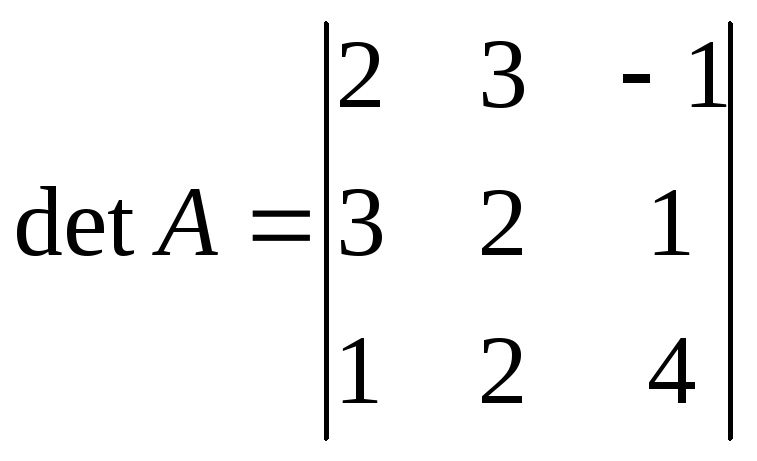Решение. Пользуясь 8-м свойством определителя матрицы, прибавим элементы третьей строки, умноженные на (-2) к элементам первой строки, а также элементы третьей строки, но умноженные на (-3), к элементам второй строки. При этом значение определителя матрицы сохранится, но два элемента первого столбца окажутся нулями.

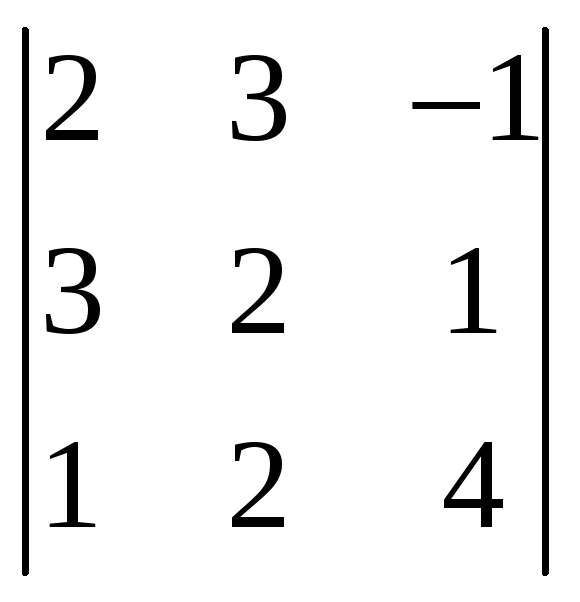
. Свойство алгебраических дополнений соседних строк

Сумма произведений элементов какой-нибудь строки (столбца) на __________________________________ соответствующих элементов _________ строки (столбца) равна _________.

2.2. Основные операции над матрицами и их свойства

Определение 2.1. Две матрицы ______________ порядка называются ______________________________________________________________.

Замечание 2. Две ______________ квадратные матрицы ________________ размера _______________________________________

; .

Определение 2.2.

1) Суммой матриц одинакового размера и называется матрица ______, полученная __________________________________ данных матриц.

2) Произведением матрицы на число называется матрица ______, полученная ____________________________________ на число .

Замечание 3. Сложение матриц и умножение матрицы на число называются ______________________________ с матрицами. __________ матриц ____________ порядка ___________________________________.

Замечание 4. В отличие от матриц, _______________________ элементы, а __________________________ (столбца) ________________ на число .

Пример 2.1. Сложить матрицы и .

Решение. Воспользуемся определением 2.2 (1):

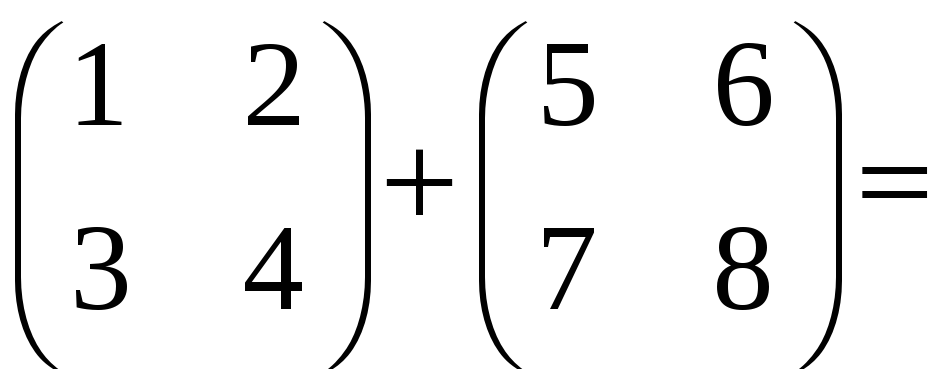
Пример 2.2. Умножить матрицу на число 5.

Решение. Воспользуемся определением 2.2 (2)

2.2.1. Свойства линейных операций над матрицами

Пусть А, В, С – матрицы одинакового размера, – числа.

– переместительное свойство сложения матриц (_______________________);

– сочетательное свойство сложения матриц (________________________);

– ________________ умножения ______________________;

– распределительное свойство умножения матрицы на число ____________________________ (_________________________);

– _______________________ умножения матрицы на число __________________________.

Благодаря этим свойствам при выполнении многих операций с матрицами можно обращаться ________________________________.

Примеры 2.3. 1) Пусть , , вычислить . 2) Пусть 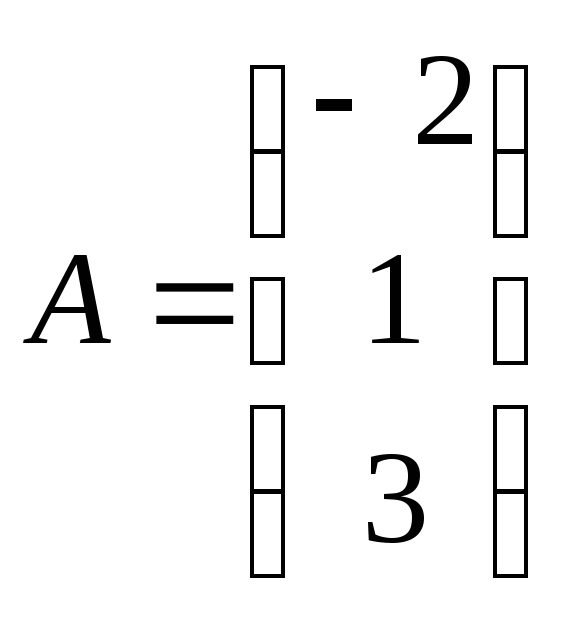, , 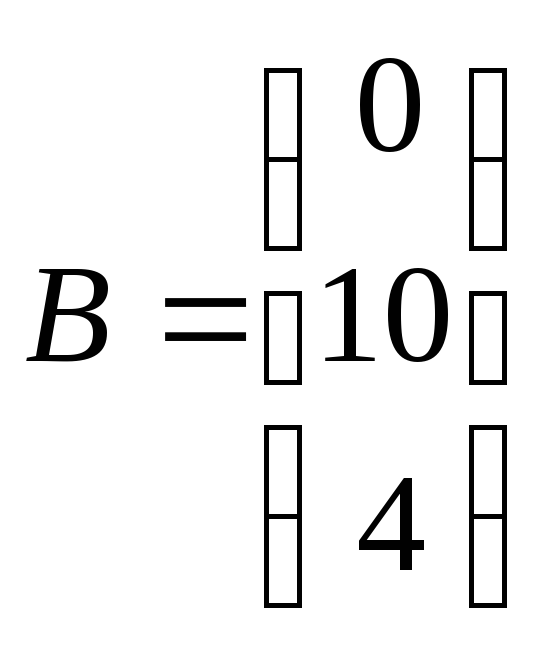вычислить .

Решение.

1).

2).

2.2.2. Умножение матриц

Определение 2.3. Произведением матрицы на матрицу называется матрица с элементами:

, , , (2.1)

где - сумма произведений элементов _-ой строки ________ матрицы на соответствующие по порядку элементы _-го столбца ________ матрицы.

Обозначение: ________________.

Замечание 5.

1) Согласно этому определению, умножать можно только такие две матрицы, когда _________________________________________________________. Произведение имеет столько строк, сколько ________ матрица, и столько столбцов, сколько ______. В противном случае произведение ______________________.

2) Произведение матриц _________________________________________.

3) Операция умножения матриц __________________________________

Пример 2.4. Умножить матрицу на матрицу .

Решение. Матрица А имеет размер ___, матрица В – ___, следовательно у матрицы размер ___.

Пример 2.5. Умножить матрицу на матрицу .

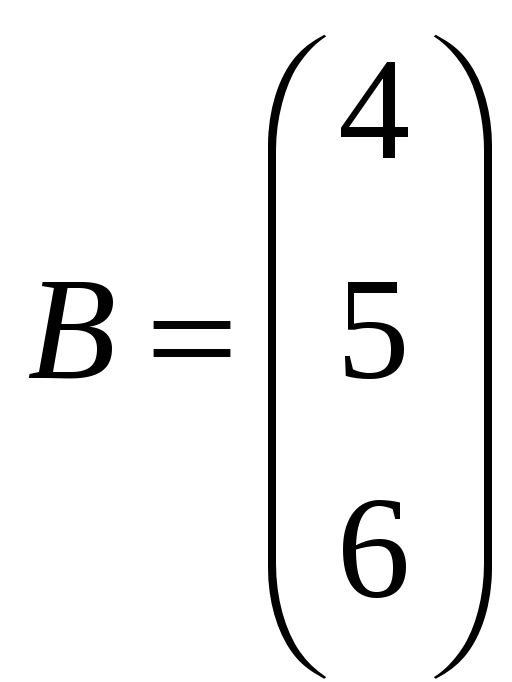Решение. Матрица А имеет размер ___, матрица В – ____, следовательно у матрицы размер ___.

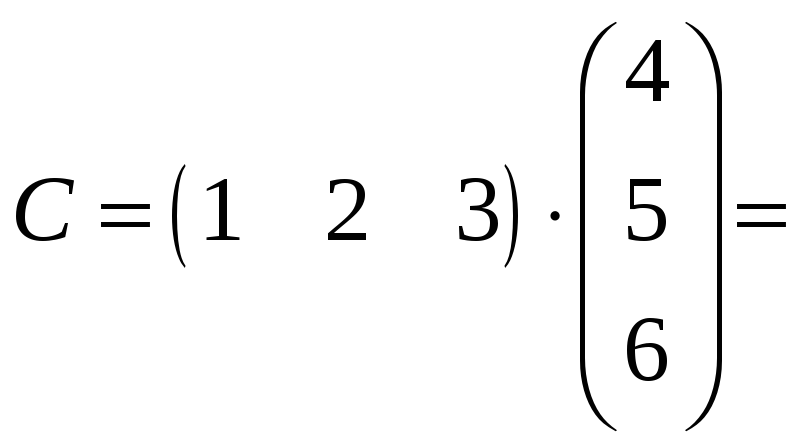
Пример 2.6. Умножить матрицу на матрицу .

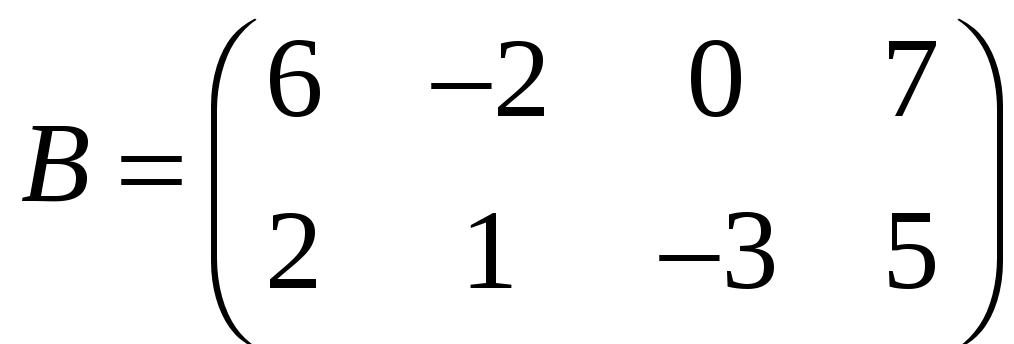Решение. Воспользуемся формулой (2.1):

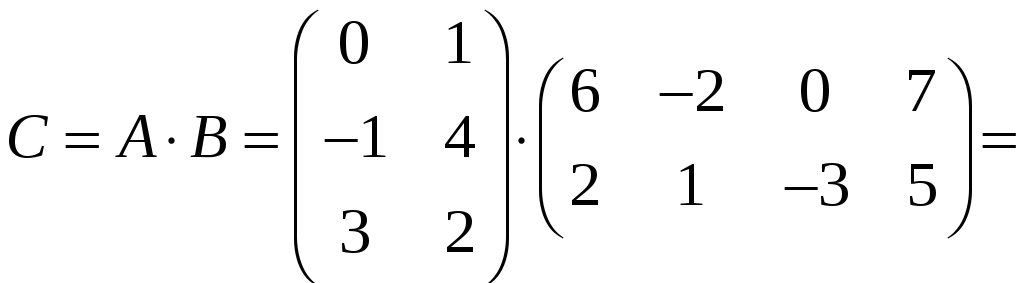
Пример 2.7. Пусть Вычислить ,

Решение. .

Определение 2.4. Матрица, полученная из матрицы А размера mхn заменой строк на соответствующие столбцы, называется транспонированной матрицей и обозначается __.

.

Замечание 6. Матрица __ имеет размер ___.

Пример 2.8. ,

Решение.

Свойства умножения матриц

Пусть, размеры матриц таковы, что произведения матриц определены.

1) – __________________ умножения;

2) 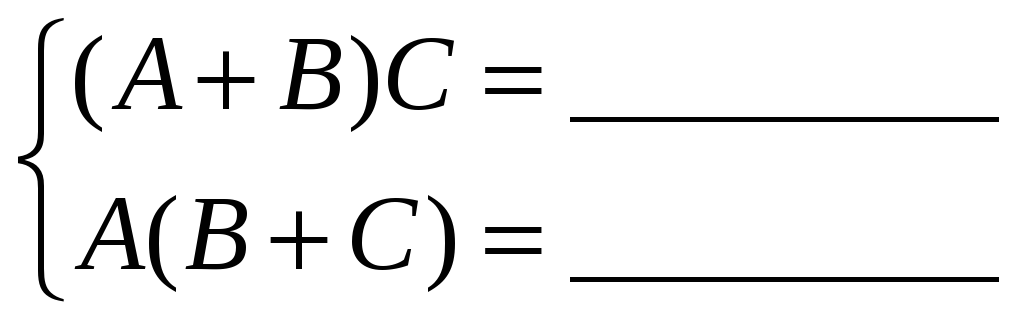– дистрибутивность умножения матриц относительно суммы матриц.

7