03-09-2014_06-10-43 Рабочая тетрадь / Lecture_1s_1k-5konspekt
.docxЛекция 5
5.1. Нахождение обратной матрицы методом Гаусса
Напомним, что
матрица
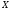называется обратной к
,
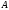если ___________. Обратные матрицы существуют
лишь для _____________ матриц, т.е.
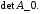Было показано, что _______________, где __ –
присоединенная матрица, полученная
__________________________, т. е. вычислением
определителей ___-ого порядка. Вместе с
тем, операция вычисления определителя,
запрограммированная в ЭВМ, требует
больших машинных ресурсов. Поэтому
более предпочтительным выглядит
вычисление обратной матрицы с помощью
метода Гаусса.
Для этого
воспользуемся определением обратной
матрицы
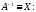
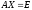
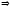
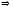
Таким образом,
матричное уравнение
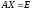эквивалентно _________
_______________________________________, каждая из которых
является системой из __ переменных и все
они имеют одну и ту же ___________ матрицу
системы:
;
;
…;
.
Все эти системы объединим в одной расширенной матрице:
.
Приведение этой
матрицы к ступенчатому виду должно
обозначать приведение к ступенчатому
виду ____________________________. Так как
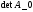
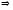
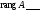
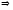она может быть приведена к следующему
виду:
.
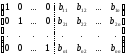Решение каждой из подсистем имеет вид:
,
,
…, 
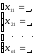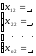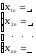
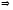
матрица
,
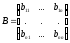стоящая за вертикальной чертой, является
_____________матрицей __.
Пример
5.1. Для
матрицы
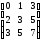найти обратную методом Гаусса.
Решение.
5.2. Понятие векторного (линейного) пространства
Определение 5.1. _______________ система _ чисел ____________, называется ____________________. Каждое число _ называется _-той ______________________________________________________________
Примеры векторов:
а) векторы-отрезки, выходящие из начала координат на плоскости или в трехмерном пространстве;
б)
коэффициенты любого линейного уравнения
с
неизвестными составляют
__________________________;
в)
если дана матрица из
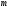строк
и
столбцов, то ее столбцы будут _-мерными,
а столбцы _-мерными ___________________.
Понятие линейного (многомерного векторного) пространства является одним из основных в современной математике.
Пусть,
–
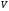некоторое множество,
–
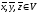элементы
,
,
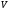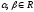причем,
1) ___________; 2) ________________.
Потребуем, чтобы эти операции удовлетворяли следующим аксиомам:
Аксиомы линейного пространства
1)
;
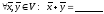2)
;
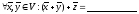3)
;
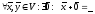4)
;
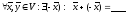5)
;
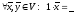6)
;
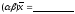7)
;
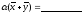8)
.
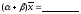Определение 5.2.
Множество
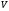элементов
,
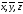в котором определены операции сложения
и умножения элемента на число,
удовлетворяющие аксиомам (1-8), называется
_______________________________________
______________________________________________________________
Определение
5.3. _____________________________
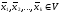с ___________________
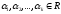называется выражение вида
_____________________.
Определение
5.4. Вектора
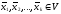называются ________________,
если
,
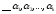из которых _________________________________, такие что
линейная комбинация
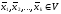с этими
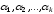является ___________________ V,
т.е.
__________________. (5.1)
Если
___________________, то вектора
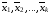называются
__________________________________
Из данного определения вытекают следующие утверждения:
1)
____ среди векторов
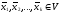есть _____________, то они _________ ____________________
Доказательство
2)
_____________ векторов
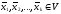_______________, то и ____ вектора ____________________
Доказательство
3)
Теорема 5.1.
Векторы
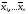___________________ тогда и только тогда, когда
_________________________________________________________
Доказательство
5.3. Базис линейного пространства
Определение
5.5. Совокупность
векторов
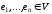называют _________ в
,
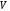если:
1)
вектора
– ____________________________;
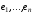2) для ______ найдутся __________________, такие, что
_________________. (5.2)
При
этом равенство (5.2) называется
_____________________________ ______________, а ____________
называются _______________
_____________________________________________.
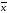Пример
5.2. Пусть
.
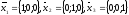Показать, что вектора линейно независимы.
Решение.
Теорема 5.2 (________________________________________).
____________ элемент ____ может быть ___________________________ ______________________________________
____________________.
Координаты вектора относительно базиса определяются ______________.
Доказательство
Теорема 5.3 (__________________________________________________).
__________________________________
,
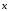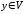_____________ (относительно любого фиксированного
базиса в
)
______________.
_________________________________________________________________ _________________________________________
Доказательство
Определение
5.6. Линейное
пространство
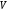называется _–мерным, если
1. В нем существуют ____________________________________________
2. ____________________________________________________________
Если
задана система
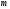векторов
…,
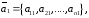
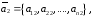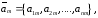где
,
,
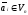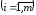а координаты заданы в одном и том же
базисе, то
–
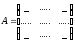матрица системы векторов, где в
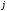-м
столбце стоят координаты вектора __.
Теорема 5.4. Для того, чтобы _ векторов _-мерного линейного пространства были _________________________________________, чтобы _____ матрицы этой системы был равен __.
Следствие
1.
________________
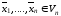тогда и только тогда, когда для данных
векторов
.
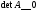Следствие 2. Если _____ матрицы системы __ векторов линейного пространства равен _, то ____________________________________________ этой системы также равно _.
Пример
5.3. Выяснить,
являются ли вектора
,
,
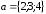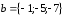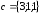линейно
зависимыми.
Решение.