
03-09-2014_06-10-43 Рабочая тетрадь / Lecture_1s_1k-6konspekt
.docЛекция 6
6.1. Система линейных однородных уравнений
Запишем систему линейных однородных уравнений
 (6.1)
(6.1)
Однородная система ________________, так как всегда имеется ________________________________________________
Согласно общей
теории, если
![]() ,
то ______________ является _________________ решение.
,
то ______________ является _________________ решение.
Если же
![]() ,
то решений ___________________, и все они,
____________________________________
,
то решений ___________________, и все они,
____________________________________
Теорема 6.1 (________________________________________________).
Система линейных _________________ уравнений _____________ матрицей имеет ________________ решение тогда и только тогда, когда определитель системы ______ нулю.
Доказательство
По теореме Крамера __________ тогда и только тогда, когда система с квадратной матрицей имеет ________________ решение (т.е. векторы – столбцы системы (6.1) – линейно ___________). В случае если задана система линейных однородных уравнений, это решение – __________________ Значит, __________________ решения имеются тогда и только тогда, когда ___________ (т.е. решений системы ___________________________).
Любое решение системы линейных однородных уравнений выражается ____________________________________________________________
(6.2)
Покажем, что вектора
_______ – _______________. Для этого составим
матрицу
![]() из их __________:
из их __________:
Ниже черты расположен
минор порядка ___, _______________
![]() _______
_______
![]() ______________ матрицы
______________ матрицы
![]() __________________.
__________________.
Следовательно, вектора ____________________, т.е. эти вектора образуют ____________________________
Определение 6.1. Всякая ________________________ система ____ решений системы линейных ______________ уравнений называется ________________________ системой решений.
Замечание 1.
Отличный от нуля минор матрицы порядка
![]() ,
такой, что всякие миноры порядка
,
такой, что всякие миноры порядка
![]() и выше, (если такие имеются) равны нулю,
называется ___________________.
и выше, (если такие имеются) равны нулю,
называется ___________________.
Итак, общее решение системы линейных однородных уравнений:
(6.3)
где _____________________________________________________,
___________________________________________________.
Пример 6.1. Решить
систему уравнений

Решение.
6.2. Системы линейных неоднородных уравнений
Рассмотрим систему __________________ уравнений
________ (6.4)
Пусть
![]() .
.
Пусть __ – решение этой системы, т.е.
______ (6.5)
Вычитая из (6.4) выражение (6.5), получим:
______________.
________ является решением соответствующего _____________ уравнения.
Согласно (6.3) ___________________________.
В нашем случае _________________________
или _____________. (6.6)
Теорема 6.2. ______________ системы линейных ______________ уравнений представляется в виде ______________________________________________ и ______________ соответствующей ей _________________ системы.
Следствие 1. _____________ двух _________________________ систем линейных ________________ уравнений является ____________ соответствующей системы линейных _______________ уравнений .
Следствие 2. ____________________________ системы линейных ________________ уравнений ________________________ соответствующей системы линейных _________________ уравнений дает ________ решение системы линейных _____________________ уравнений.
Замечание 2.
В формуле (4.7) (лк. 4)
![]() – ___________ решение системы.
– ___________ решение системы.
Пример 6.2. Решить
систему уравнений
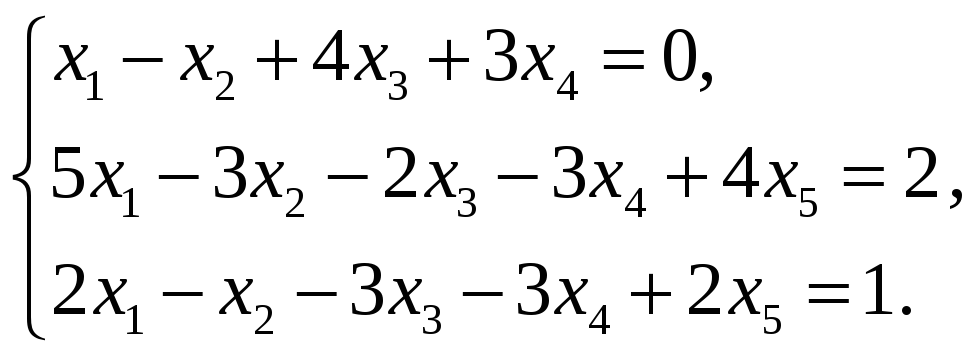
Решение.
РАЗДЕЛ II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
6.3. Основные понятия
Обозначение: множество точек прямой – _, плоскости – _, пространства – _.
Пусть точки
![]() ,
причем точки – _________________: например, А
– ________, В –
_______. Рассмотрим
отрезок прямой, расположенный между
этими точками.
,
причем точки – _________________: например, А
– ________, В –
_______. Рассмотрим
отрезок прямой, расположенный между
этими точками.
Определение 6.3. Отрезок АВ называется __________________________, если его концы А и В ___________; если при этом первой является точка _, а второй – точка _, то А – ________________, а В – ____________.
Замечание 3. a) если начало и конец вектора совпадают, то вектор называется _________ и обозначается __; б) длиной (___________) направленного отрезка ___ называется __________________.
Определение 6.4. Векторы называются ________________, если они расположены на _______ прямой или ______________________________.
Векторы называются ________________, если существует плоскость, которой они ___________________.
Замечание 4. Нулевой вектор ______________ любому другому вектору, так как ___________________________ и его длина равна __________.
Определение 6.5. Два вектора называются ________, если они ______________________________________________________________
Из определения
6.5 следует, что если задан вектор
![]() и точка
и точка
![]() ,
то можно построить
_________________________________________. Другими словами,
вектор
,
то можно построить
_________________________________________. Другими словами,
вектор
![]() можно перенести в точку __.
можно перенести в точку __.
Определение 6.6.
Пусть даны
вектора
![]() :
:
![]() .
Тогда вектор __ называется _________ векторов
.
Тогда вектор __ называется _________ векторов
![]() .
.
Обозначение. ________________.
Правила сложения
а) правило треугольника б) правило параллелограмма
Определение 6.7.
Произведением вектора
![]() на число
на число
![]()
![]() называется вектор
называется вектор
![]() ,
удовлетворяющий следующим условиям:
,
удовлетворяющий следующим условиям:
-
векторы
 и
и
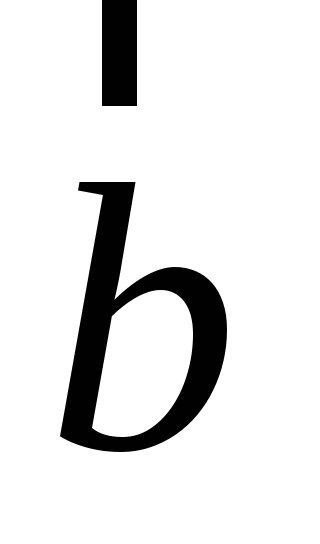 ______________, если _____ и _______________ ___________, если
_____;
______________, если _____ и _______________ ___________, если
_____; -
_____________.
Обозначение. _________.
Замечание 5. 1) произведение вектора на число 0 есть _________ вектор;
2) обозначение ______ означает, что ____________ вектора имеют место быть свойства, идентичные ___________________ векторного пространства, причем свойства __________________. Свойства 6 и 8 проверяются перебором различных вариантов. А свойство 7 следует ________________.
Теорема 6.3 (_________).
Если направленные прямые отсекают одинаковые отрезки на одной стороне угла, то они отсекают одинаковые отрезки на другой его стороне.
6.4. Базис векторов
Теорема 6.4. 1) вектор _____________________ тогда и только тогда, когда он равен ______; 2) векторы ________________________ тогда и только тогда, когда они ________________; 3) векторы _______________________ тогда и только тогда, когда они _________________; 4) любые _________ вектора ____________________.
Следствия
1) _______________________________________________________________;
2) в __ базис состоит из __________________________________________;
3) в __ базис образует ______________ пара _________________ векторов;
4) в __ базис – _________________ тройка __________________ векторов.
Замечание 6.
Требование упорядоченности означает,
что, например в
![]() ,
,
![]() и
и
![]() –
________ базисы.
–
________ базисы.
6.5. Проекция вектора на ось
Определение 6.8.
Осью
![]() назовем прямую, по которой _________________.
________________________________ (направляющий вектор
оси), который является __________________ вектором
и обычно берется _____________.
назовем прямую, по которой _________________.
________________________________ (направляющий вектор
оси), который является __________________ вектором
и обычно берется _____________.
Определение 6.9.
_____________
точки
![]() на ось
на ось
![]() называется точка
называется точка
![]() ,
получаемая
__________________________________________________
_______________________________________________________________
,
получаемая
__________________________________________________
_______________________________________________________________
Определение
6.10. ____________
вектора
![]() на ось
на ось
![]() называется число _______, где точки
называется число _______, где точки
![]() и
и
![]() - _________________________________________
- _________________________________________
_______________ , (6.1)
причем
![]() ,
если
,
если
![]() ,
,
![]() ,
если
,
если
![]() .
.
Свойства проекции
1) проекция
вектора
![]() на ось
на ось
![]() равна __________________________
______________________________________________________________
равна __________________________
______________________________________________________________
_______________
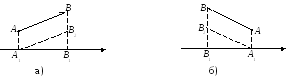
L L
2) проекция ________ векторов на ось равна __________________________:
_________________
Действительно, это очевидно из следующих рисунков:
3) ________________________ вектора _________ равна __________________________________________________________________
______________.
.
