03-09-2014_06-10-43 Рабочая тетрадь / Lecture_1s_1k-3konspekt
.docЛекция 3
3.1. Единичная и нулевая матрицы
Определение 3.1.
_______________
матрица
размера
называется ______________ матрицей.
Замечание 1.
Если матрица A
квадратная, то
.
Если матрица
размера
,
то
.
Если матрица
размера
,
то
.
Покажем справедливость равенства _______.
Определение 3.2. Матрица, все элементы которой равны ______, называется _____________ матрицей
Очевидно, что ____________________
3.2. Решение системы линейных алгебраических уравнений (СЛАУ)
3.2.1. Обратная матрица и ее свойства
Пусть задана система n линейных уравнений с n неизвестными
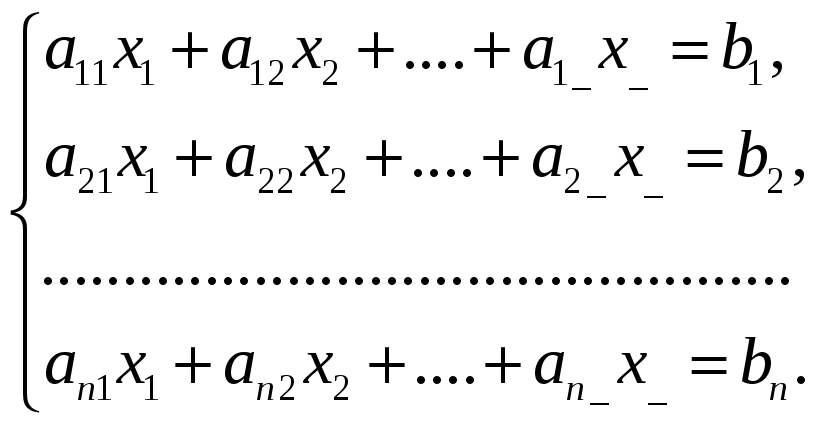(3.1)
Определение 3.3.
. ____________
матрица __ называется ___________ по отношению
к матрице
системы (3.1), если выполняется равенство
_____________________, где __ –
единичная матрица.
Определение 3.4.
_____________
матрица
называется _______________, или ____________, если
____________. Если _____, то матрица называется
______________ (_____________).
Теорема 3.1. . ______________________________________________________, определяемую формулой:
(3.2)
Доказательство
По определению
3.3 
.
Но здесь
_______________________ – есть разложение
определителя
по его первому столбцу, потому является
значением _. Таковы же все элементы
главной диагонали. Так, ___________________ –
есть разложение определителя по
-ому
столбцу. Значит, все элементы главной
диагонали равны _.
Все элементы вне
главной диагонали представляют собой
суммы произведений элементов
___________________ определителя
на алгебраические дополнения
соответствующих элементов _________________ и
потому равны ______.
Значит, __________________.
Замечание 1. В равенстве (3.2) матрица
получена из матрицы
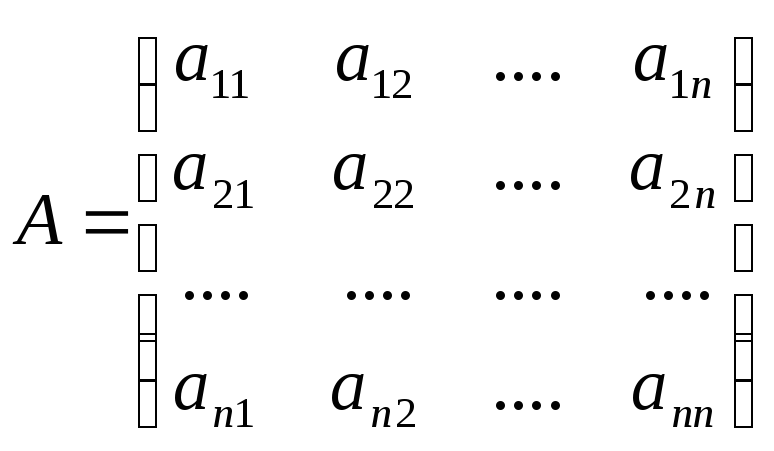заменой ее элементов на
_______________________________________________________________
_________________. Такая матрица __ называется
_____________________ (____________) матрицей для
матрицы
.
Таким образом,
Пример 3.1. Для
матрицы
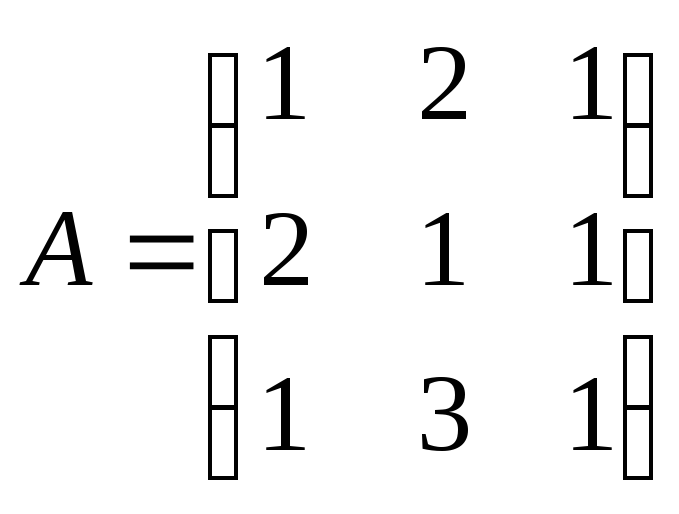найти обратную матрицу
Решение.
3.2.2. Матричный способ решения системы (3.1)
Назовем
(3.3)
матричным уравнением системы (3.1)
или __________, (3.4)
где
Покажем, как найти решение системы (3.1) с помощью обратной матрицы.
Каждую часть равенства (3.4) умножим _____________________________
____________________ (3.5)
– решение системы (3.1).
Запишем (3.5) в развернутом виде:
Таким образом, из определения равенства матриц следует:
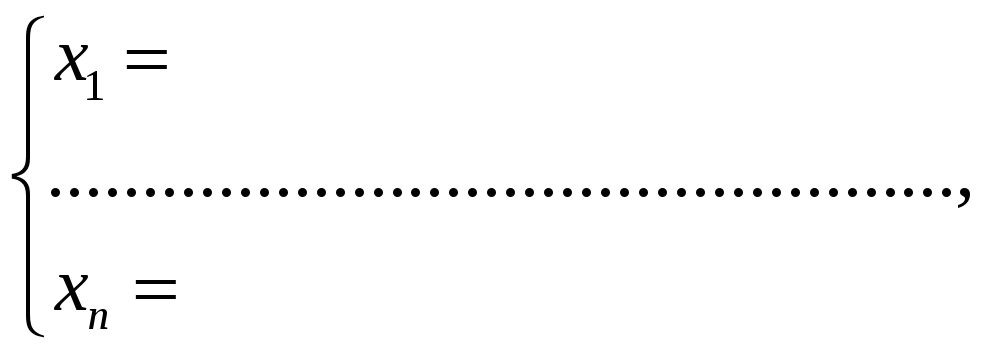(3.6)
Пример 3.2. Решить
систему
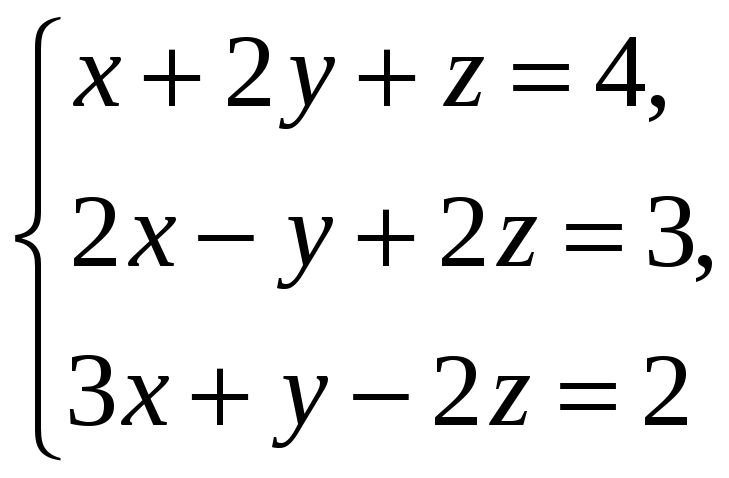матричным способом.
Решение.
.
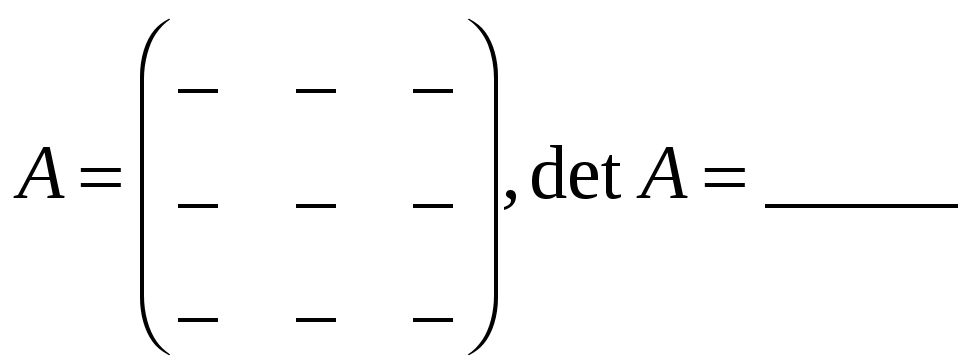Далее вычисляются алгебраические дополнения, и составляется матрица __.
,
тогда
3.2.3. Решение системы (3.1) по формулам Крамера
Определение 3.5. Определитель матрицы, составленный ________________ __________________, называется __________ определителем системы (3.1):
________________ - ______________ определители, которые составляются следующим образом: при составлении ___ в определителе _ _-й столбец _________________________, например:
Возвращаясь к формулам (3.6), нетрудно заметить, что суммы, стоящие в числителях есть ни что иное, как ________________________, разложенные _____________________________ и тогда формулы (3.6) примут вид:
(3.7)
– формулы ______________.
Пример 3.3. Решить систему линейных уравнений из примера 3.1 с помощью формул Крамера.
Решение.
,
Теорема 3.2 (_____________).
Система (3.1)
________________ матрицей
имеет решение, притом _______________________,
тогда и только тогда, когда _____________.
3.3. Ранг матрицы
Определение 3.6. Определитель с элементами, стоящими _______________ ____________________________________ матрицы, называется __________ _ -го порядка этой матрицы.
Замечание 1. _________________________________________
Пример 3.4.
.
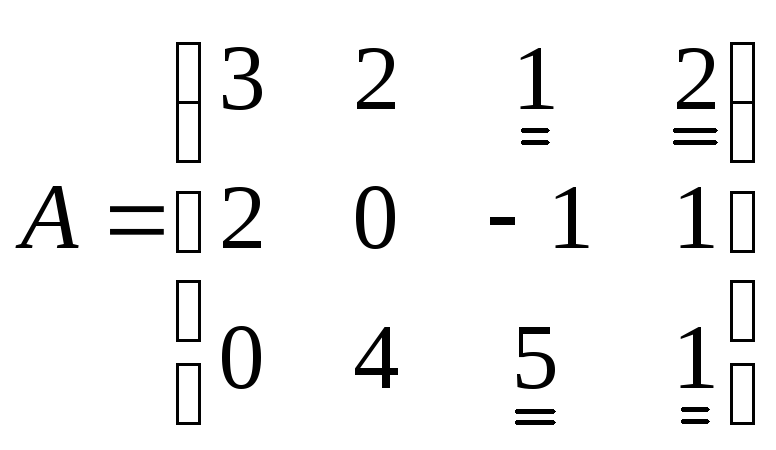Здесь
,
,
– миноры ____________.
Определение 3.7. ___________________________________________________ ___________________________________
Обозначение: __________. (3.8)
Таким образом, обозначение (3.8) означает, что среди __________________ _________________________________________________________________________________________________________________________________
Определение 3.8. Каждый ___________________________________ которого совпадает ________ матрицы, называется ___________ минором.
Замечание 3. У матрицы может быть _________________________________.
Определим ранг матрицы из примера 3.4.
Легко проверить, что в матрице все миноры 3-го порядка равны нулю (проверить самостоятельно):
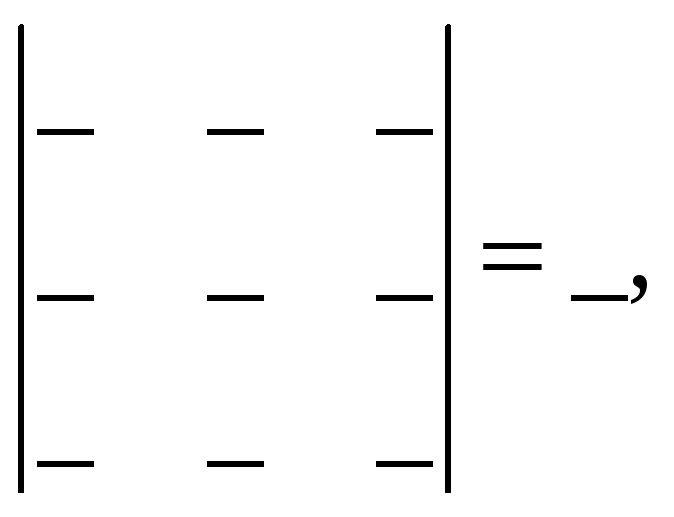
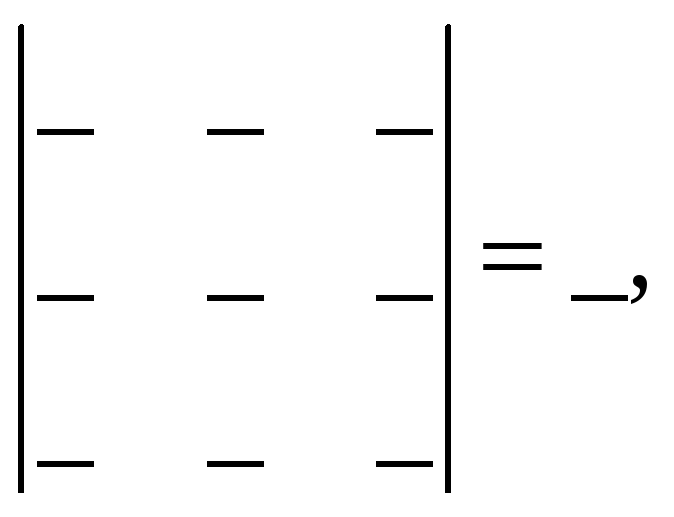
но имеются отличные
от нуля миноры __-го порядка, значит,
.