
5_УМК
.PDFПоследнее равенство выполняется во всех точках экстремума. Подберем λ так, чтобы для значений x и y , соответствующих экстремуму функции z, вторая скобка в равенстве (1.36) обратилась в нуль:
|
∂f |
+ λ |
∂ϕ = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
∂y |
∂y |
|
|
|
|
|
|
Но тогда при этих значениях x и y из равенства (1.36) следует равенство |
||||||||
|
∂f + λ |
∂ϕ = 0 . |
|
|
|
|
|
|
|
∂x |
∂x |
|
|
|
|
|
|
Таким образом, получается, что в точках экстремума удовлетворяются три |
||||||||
уравнения: |
∂f |
+ λ ∂ϕ = 0 |
|
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|||
|
|
|
∂x |
|
∂x |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
∂f |
+ λ |
∂ϕ |
= 0 |
|
|
|
|
|
|
|
(1.37) |
||
|
|
|
∂y |
∂y |
||||
|
|
|
|
|
|
|
||
|
|
|
|
ϕ(x, y) = 0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с тремя неизвестными x, y, λ . Из этих уравнений определяем x, y и λ .
Из вывода следует, что уравнения (1.37) являются необходимыми условиями условного экстремума, но не при всяких x, y и λ , удовлетворяющих уравнениям (1.37), будет иметь место условный экстремум. Поэтому требуется дополнительное исследование характера критической точки.
Заметим, что левые части уравнений системы (1.37) являются частными
производными функции |
|
F(x, y,λ) = f(x, y) + λϕ(x, y) |
(1.38) |
по переменным x , y и λ .
Таким образом, для того чтобы найти значения x и y , удовлетворяющие условию (1.33), при которых функция z = f(x, y) может иметь условный макси-
мум или условный минимум, нужно составить вспомогательную функцию (1.38), приравнять к нулю ее частные производные по x, y,λ и из полученной системы уравнений (1.37) определить искомые x, y и вспомогательный множитель λ .
Отметим, что λ называют множителем Лагранжа, а сам метод решения задачи - методом множителей Лагранжа.
Рассмотренный метод распространяется на исследование условного экстремума функции любого числа переменных.
Пусть требуется найти экстремумы функции n переменных
u = f(x1 , x2 ,..., xn ) при условии, что переменные x1 , x2 ,..., xn связаны m
(m < n) уравнениями
31
ϕ |
1 (x1 , x2 ,..., xn ) = 0 |
|
||
|
ϕ |
2 (x1 , x2 |
,..., xn ) = 0 |
|
|
(1.39) |
|||
|
|
|
. |
|
KKKKKKKKK |
|
|||
|
ϕm (x1 , x2 |
,..., xn ) = 0 |
|
|
|
|
|||
Составим функцию F(x1 , x2 ,K, x n , λ1 , λ2 ,K, λm ) = f (x1 , x2 ,K, x n ) +
+ λ1ϕ1 (x1 ,K, xn )+K+λm ϕm (x1 ,K, xn ) и приравняем нулю ее частные производные по x1 , x2 ,K, xn :
|
∂f |
|
|
|
∂ϕ1 |
|
|
∂ϕm |
|
|
|
|
|
|
|
+ λ |
1 ∂x1 |
+K+λm ∂x1 |
= 0 |
|
|||
∂x1 |
|
||||||||||
|
∂f |
|
|
|
|
∂ϕ1 |
|
|
∂ϕm |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
+ λ |
1 ∂x2 |
+K+λm ∂x2 |
= 0. |
(1.40) |
|||
∂x2 |
|
||||||||||
KKKKKKKKKKKKK |
|
||||||||||
|
∂f |
|
|
+ λ |
|
∂ϕ |
+K+λ |
|
∂ϕm |
= 0 |
|
|
|
|
|
|
|
|
|
|
|||
∂xn |
|
|
1 ∂xn |
m ∂xn |
|
||||||
|
|
|
|
|
|
|
|||||
Из систем уравнений (1.38) и (1.39) определяем x1 , x2 ,K, xn и вспомога-
тельные неизвестные λ1 ,λ 2 ,K,λm . Так же как и для функции двух переменных,
вопрос о том, будет ли при найденных значениях x1 , x2 ,K, xn функция иметь максимум или минимум или не будет иметь ни того, ни другого, мы в общем слу-
чае оставляем открытым. На практике само содержание задачи помогает опреде-
лить характер критической точки.
ПРИМЕР 1.20 Из данного куска жести площадью 2a надо сделать закры-
тую коробку в форме параллелепипеда, имеющую наибольший объем.
Решение. |
Обозначим длину, ширину и высоту коробки через x, y, z . Зада- |
|
ча сводится к |
разысканию максимума функции V = xyz при |
условии, что |
2xy + 2xz + 2yz = 2a . Здесь мы имеем задачу на условный экстремум: |
||
найти максимум функции |
|
|
|
V = xyz |
(1.40) |
при условии, что |
|
|
|
xy + xz + yz − a = 0 (x > 0, y > 0, z > 0) . |
(1.41) |
Составим вспомогательную функцию |
|
|
|
F(x, y, z,λ) = xyz + λ(xy + xz + yz − a). |
(1.42) |
Найдем ее частные производные и приравняем их нулю:
32

yz + λ(y + z) = 0
|
|
xz + λ(x + z) = 0 |
|
|
xy + λ(x + y) = 0 |
|
|
+ + − =
xy xz yz a
. (1.43)
0
Задача сводится к решению системы четырех уравнений с четырьмя неиз-
вестными x, y, z,λ . Для решения этой системы умножим первое из уравнений
(1.43) на x , второе - на y , третье - на z, сложим их и с учетом равенства (1.41)
находим λ = − 3xyz . Найденное значение λ подставим в первые три уравнения
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
системы (1.43) и получим |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
yz 1 − |
|
|
|
|
|
(y + z) = 0 |
|
|
|
|
|
|
||||||||||||||||
|
|
2a |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
3y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
xz 1 − |
|
(x |
+ z) = 0 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
2a |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
3z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
xy 1 − |
|
(x |
+ y) = 0 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
2a |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Так как |
x, y, z по смыслу задачи отличны от нуля, то из этих уравнений |
||||||||||||||||||||||||||||
имеем |
|
3x |
(y + z) = 1, |
|
3y |
(x + z) = 1, |
3z |
(x + y) = 1. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
2a |
||||||||||||
Из первых двух уравнений находим x = y , из второго и третьего уравнений |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
y = z. Но в таком случае из уравнения (1.41) получаем x = y = z = |
a |
. |
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
a |
|
|
|
|
a |
|
|
|
|
a |
|
|
|
|
|
|
|
|||||||
Точка |
|
|
; |
|
|
; |
|
|
|
|
является единственной критической точкой, в кото- |
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
3 |
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
||||||||||||
рой функция (1.40) может иметь максимум или минимум. Так как поставленная задача имеет определенное решение, а критическая точка только одна, то в этой точке функция будет иметь максимум. Итак, для того чтобы объем коробки был
a
наибольшим, эта коробка должна быть кубом, ребро которого равно 
 .
.
3
33

1.15 ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
Пусть задана дифференцируемая функция u = u(x, y, z) . Рассмотрим точку
M(x, y, z) и вектор a , выходящий из точки M в направлении единичного векто-
ра
a0 = cosα i + cosβ j + cos γ k ,
где α,β, γ − углы, образованные вектором a0 с осями координат.
Пусть M1 (x + x, y + y, z + z) − какая-нибудь другая точка вектора a . Разность значений функции u = u(x, y, z) в точках M1 и M назовем прира-
щением этой функции в направлении вектора |
a |
и обозначим через |
|
a u . Тогда |
|||||||||||||
a u = u(x + x, y + y, z + z) − u(x, y, z) |
|
|
|
|
|
|
|
||||||||||
Обозначим через a расстояние между точками M и M1 : |
a = |
|
MM1 |
|
. |
||||||||||||
|
|
||||||||||||||||
ОПРЕДЕЛЕНИЕ 1.23 Производной функции u = u(x, y, z) в точке |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a u |
||||||
M(x, y, z) по направлению вектораa называется предел lim |
|||||||||||||||||
|
|
. |
|
|
|||||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
a→0 |
|
a |
||||||
Производная функции u по направлению вектора |
a |
обозначается символом |
|||||||||||||||
∂u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂l . Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u |
= lim |
a u |
(1.45) |
||||||||||||||
∂a |
|
. |
|
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||||
a→0 |
a |
|
|
|
|
|
|
|
|||||||||
Заметим, что если производная функции u(x, y, z) в точке |
|
M(x, y, z) по |
|||||||||||||||
направлению a положительна, то данная функция в этом направлении возрастает;
если же ∂u < 0 , то данная функция в направлении вектора a убывает.
∂a
Выведем формулу для вычисления производной по направлению. Прежде всего заметим, что приращения x, y, z координаты точки M связаны с дли-
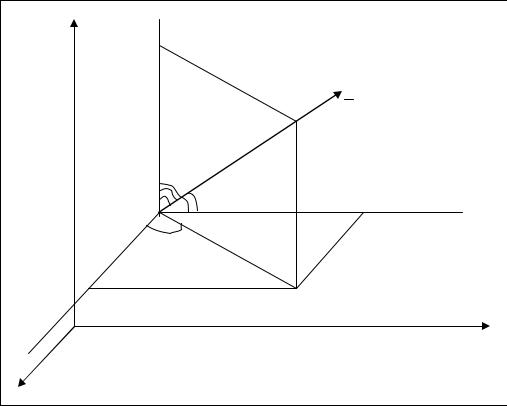
ной отрезка M1 M = a и направляющими косинусами вектора a следующими соотношениями (рис. 1.8):
x = a cosα, y = a cosβ, z = a cos γ . |
(1.46) |
34
|
z |
|
|
|
|
|
|
a |
|
|
|
γ |
M1 |
|
|
|
|
|
|
|
M |
β |
|
|
|
|
|
|
|
|
|
α |
x |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
y |
|
x |
|
Рис. 1.8 |
|
|
|
|
|
|
|
Так как функция u по условию дифференцируема, то ее приращение |
a u в |
|||
точке M(x, y, z) можно представить в виде |
|
|
||
a u = |
∂u |
x + ∂u |
y + |
∂u |
z + α1 x + α2 y + α3 z , |
(1.47) |
|||||
|
∂x |
|
|
∂y |
|
∂z |
|
|
|
|
|
где α1 → 0, α2 |
→ 0, α3 → 0 при |
x → 0, |
y → 0, z → 0. |
|
|||||||
Отсюда в силу соотношений (1.46) получаем |
|
||||||||||
∂u |
cosα + |
∂u |
cosβ + |
∂u |
|
|
(α1 cosα + α2 cosβ + α |
3 cos γ ) a |
|||
a u = |
∂y |
∂z |
cos γ a + |
||||||||
∂x |
|
|
|
|
|
|
|
a → 0 , по- |
|||
Разделив обе части этого равенства на |
a и переходя к пределу при |
||||||||||
лучим искомую формулу для производной функции в данном направлении: |
|||||||||||
∂u = lim |
a u |
= |
∂u cosα + ∂u cosβ + |
∂u cos γ |
|
||||||
|
|
||||||||||
∂a |
a→0 |
|
a |
|
∂x |
|
∂y |
|
∂z |
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u = |
∂u cosα + |
∂u cosβ + ∂u cos γ . |
(1.48) |
||||||
|
|
∂a |
∂x |
|
∂y |
∂z |
|
||||
35

Следствие. Из формулы (1.48) следует, что частные производные функции
u = u(x, y, z) |
∂u ; |
∂u ; |
∂u |
это частный случай производной по направлению. |
|
∂x |
∂y |
∂z |
|
Так, например, если a = i = {1,0,0}, то есть cosα = 1, cosβ = 0, cos γ = 0 и,
∂u = ∂u
следовательно, ∂a ∂x .
∂u
Замечание Производная по направлению ∂a , вычисленная в т. M 0 − это
скорость изменения функции u = u(x, y, z) в направлении вектора a в данной
точке.
ПРИМЕР 1.21 Найти производную функции u = xy + yz + 1 по направле-
нию вектора |
|
|
|
= {12;−3;−4} в точке M(0;−2;−1) . |
|
|
|
|
|
|
||||||||||||||||||||||||
a |
|
|
|
|
|
|
||||||||||||||||||||||||||||
Решение. |
Найдем |
частные |
производные |
|
функции |
u = xy + yz + 1: |
||||||||||||||||||||||||||||
∂u = y; |
∂u = x + z; |
∂u = y . Эти производные в точке M(0;−2;−1) имеют зна- |
||||||||||||||||||||||||||||||||
∂x |
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
чения: |
∂u |
|
|
|
= −2; ∂u |
|
|
|
|
= −1; ∂u |
|
|
= −2 . Теперь найдем направляющие коси- |
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
∂x |
|
M |
|
|
|
|
|
∂y |
|
|
M |
∂z |
|
M |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
нусы вектора |
a |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; cosβ = − 3; cosγ = − 4 . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= 13; cosα = |
12 |
|||||||||||||||||||||
|
|
|
|
|
= |
122 |
+ (− 3)2 |
+ (− 4)2 |
||||||||||||||||||||||||||
|
|
a |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
13 |
|
13 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
После этого, по формуле (1.48), вычисляем производную |
|
|
|
|||||||||||||||||||||||||||||||
|
∂u |
|
|
= (− 2) |
12 |
|
|
|
− 3 |
− 4 |
|
− 24 + 3 + 8 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ (− 1) |
|
|
|
|
+ (− 2) |
= |
|
|
= −1. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
∂a |
M |
|
|
|
|
|
|
13 |
|
|
13 |
13 |
|
13 |
|
|
|||||||||||||||||
Замечание Для функции двух переменных u = u(x, y) производная по на- |
||||||||||||||||||||||||||||||||||
правлению вектора |
|
= {cosα,cosβ} в точке M(x, y) |
|
|||||||||||||||||||||||||||||||
a |
выводится аналогично и |
|||||||||||||||||||||||||||||||||
вычисляется по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u = ∂u cosα + ∂u cosβ . |
|
|
|
|
|
(1.49) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂a |
∂x |
|
|
|
|
∂y |
|
|
|
|
|
|
|||||
|
u = |
|
|
|||||||||||||||||||||||||||||||
ПРИМЕР 1.22. Найти производную функции |
x2 + y2 |
в точке |
||||||||||||||||||||||||||||||||
M(3;4) по направлению биссектрисы первого координатного угла. |
|
|
||||||||||||||||||||||||||||||||
Решение. Найдем частные производные функции u = 
 x2 + y2 :
x2 + y2 :
36

∂u = |
|
|
x |
|
; |
∂u = |
|
|
|
|
y |
|
|
. Эти |
производные |
в точке M(3;4) имеют |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
∂x |
x2 |
+ y2 |
|
|
∂y |
|
|
x2 |
+ y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
значения: |
∂u |
|
|
= |
|
|
3 |
|
|
|
|
= |
3 |
|
; |
|
∂u |
|
|
= |
|
|
4 |
= |
4 |
|
. Направляющий век- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
∂x |
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
||||||||||||
|
|
|
|
M |
|
|
32 |
+ 42 |
|
|
5 |
|
|
|
M |
32 |
+ 42 |
5 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
тор биссектрисы первого координатного угла - это вектор, который составляет с положительными направлениями осей Ox и Oy углы α = 450 и β = 450 . Значит
cosα = |
|
2 |
; cosβ = |
|
2 |
. Тогда, по формуле (1.49) |
||||||||||||||||||||||||
2 |
|
|
2 |
|||||||||||||||||||||||||||
∂u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
3 |
|
4 |
|
7 |
|
|
|
||||
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
||||||||||
|
|
|
= |
|
|
|
|
|
+ |
|
|
|
|
= |
|
|
|
|
|
|
+ |
|
|
= |
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
∂a |
|
M |
|
5 |
|
|
2 5 |
|
2 |
|
2 |
|
|
5 |
|
5 |
|
10 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1.16 ГРАДИЕНТ
Пусть задана дифференцируемая функция трех переменных u = u(x, y, z) ОПРЕДЕЛЕНИЕ 1.24 Вектор, координатами которого являются частные
производные первого порядка функции u = u(x, y, z) в точке M(x, y, z) , называ-
ется градиентом данной функции и обозначается:
|
|
|
grad u = |
∂u |
|
+ |
∂u |
j + ∂u |
|
|
|
|||
|
|
|
i |
k |
(1.50) |
|||||||||
|
|
|
|
|
|
∂x |
∂y |
∂z |
|
|||||
|
|
|
∂u ∂u |
; |
∂u |
|
|
|
|
|
||||
или кратко grad u = |
; |
∂y |
. |
|
|
|
|
|
||||||
|
|
|
∂x |
|
|
∂z |
|
|
|
|
|
|||
Докажем теорему, устанавливающую связь между градиентом и производ- |
||||||||||||||
ной по направлению. |
|
|
|
|
|
|
|
|
|
|
|
|||
Теорема 1.8. Пусть в некоторой области D R3 задана дифференцируемая |
||||||||||||||
функция u = u(x, y, z) , |
для |
которой в |
каждой точке области |
D существует |
||||||||||
∂u |
∂u ∂u |
|
|
|
|
|
|
|
|
|
|
|
||
grad u = |
; |
; |
. Тогда производная функции u = u(x, y, z) по направле- |
|||||||||||
|
∂x |
∂y |
∂z |
|
|
|
|
|
|
|
|
|
|
|
нию вектора |
|
|
|
= {a1 ,a 2 ,a 3 } есть проекция вектора grad u на вектор |
a |
. |
|
|||||||||||||||||||||||||||||||||||||||
a |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Доказательство. Рассмотрим единичный вектор |
a |
0 , соответствующий век- |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
cosα = |
|
a1 |
|
; cosβ = |
a 2 |
; cos γ = |
a 3 |
, |
|
||||||||||||||||||||||||
тору |
|
a: |
|
|
a |
|
|
= |
a12 + a 22 |
+ a 32 |
; |
|
тогда |
|||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
0 = {cosα;cosβ;cos γ} , |
|
|
|
|
|
|
|
= |
|
|
|
|
a |
|
|
|
|
|
|
|
a |
|
|
|
|
|
a |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
причем |
|
a |
0 |
|
|
|
cos2 α + cos2 β + cos2 γ |
= 1. |
Вычис- |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
a |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
лим скалярное произведение векторов grad u и |
a |
0 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
37
|
|
( |
|
|
u |
|
0 ) = ∂u cos α + |
∂u cosβ + |
∂u cos γ . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
grad |
a |
(1.51) |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
∂y |
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Выражение, стоящее в правой части этого равенства, есть производная от |
||||||||||||||||||||||||||||||||||||
функции u = u(x, y, z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
u |
|
|
0 ) = ∂u . |
||||||||||||
по направлению вектора |
|
|
. Значит |
grad |
||||||||||||||||||||||||||||||||
a |
a |
|||||||||||||||||||||||||||||||||||
Обозначим через ϕ угол между векторами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂a |
|||||||||||||||||
grad |
u и |
a |
0 , тогда |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
∂u |
= |
( |
|
|
|
|
|
) |
= |
|
|
|
|
|
|
cos ϕ = |
|
|
|
|
|
|
cos ϕ |
(1.52) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
grad u |
a 0 |
gradu |
|||||||||||||||||||||||||||||
∂a |
|
grad u a 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u = пр |
|
|
|
|
|
|
|
||||
|
|
|
||||||||||||||||||||||||||||||||||
Последнее соотношение и доказывает теорему, т.е. |
|
|
grad |
u . |
||||||||||||||||||||||||||||||||
a |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂a |
|
|
|
|
|
|
|
|
|
|
Следствие 1 Из всех производных по направлению, вычисленных для функции в одной и той же точке, наибольшее значение имеет та
производная, которая вычислена в направлении градиента.
Доказательство. Из соотношения (1.51): наибольшее значение у производ-
∂u
ной ∂a будет при cosϕ = 1, то есть ϕ = 0, а это и означает, что направление
вектора a совпадает с направление вектора grad u . Причем это наибольшее зна-
∂u
чение производной ∂a в направлении градиента равно grad u .
Следствие 2 Производная по направлению вектора, перпендикулярного к вектору grad u , равна нулю.
Доказательство. Данное утверждение следует из соотношения (1.52), если
cosϕ = 0, т.е. ϕ = π . 2
Замечание Для дифференцируемой функции двух переменных u = u(x, y)
градиент определяется формулой
grad u = |
∂u |
|
+ |
∂u |
|
|
|
i |
j. |
(1.53) |
|||||
|
∂x |
∂y |
|
||||
38

ПРИМЕР 1.23 В каком направлении должна двигаться точка M(x, y, z) при
переходе через точку M 0 |
(− 1;1;−1) , чтобы функция u = |
x |
+ + |
y |
+ |
z |
менялась с |
y |
|
|
|||||
|
|
|
z x |
||||
наибольшей скоростью?
Решение. В соответствии со следствием 1 функция u = u(x, y, z) будет ме-
няться с наибольшей скоростью в направлении вектора grad u , координаты кото-
рого вычислены в точке M 0 . Итак, находим частные производные
|
|
|
|
∂u = |
1 |
− |
z |
; |
∂u = − |
x |
|
|
+ |
1 |
; |
|
∂u = − |
y |
|
+ |
1 |
|
и вычислим их в точке |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
y2 |
|
|
|
z2 |
|
x |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∂x y x2 |
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
z |
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
M 0 (− 1;1;−1) : |
∂u |
|
|
|
|
= 2; |
|
∂u |
|
|
|
|
= 0; |
∂u |
|
|
= −2 . В результате получим век- |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
M 0 |
|
|
|
∂y |
|
M |
0 |
|
|
|
|
|
∂z |
|
M |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
тор grad u |
|
M |
0 |
= {2;0;−2}, который и является ответом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ПРИМЕР 1.24 С какой наибольшей скоростью может меняться функция |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
u = ln(x2 − y2 + z2 ) |
при переходе точкиM(x, y, z) через точку M(1;1;1)? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Решение. Также в соответствии со следствием 1, необходимо вычислить ко- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ординаты вектора grad u в точке M 0 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
∂u = |
|
|
1 |
|
|
|
|
|
|
|
|
|
2x; |
∂u = |
|
|
|
1 |
|
|
|
( |
− 2y); ∂u = |
|
|
|
|
|
1 |
|
|
|
|
|
2z |
|||||||||||||||||||||||||
|
|
− y2 + z2 |
|
|
2 − y2 + z2 |
|
|
|
|
− y2 + z2 |
||||||||||||||||||||||||||||||||||||||||||||||||||
∂x x2 |
|
|
|
∂y x |
|
|
|
|
|
|
∂z x2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
∂u |
|
|
= 2; |
|
∂u |
|
|
|
|
|
|
|
|
= −2; |
∂u |
|
|
|
|
= 2 . А теперь, чтобы получить ответ на постав- |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
∂x |
|
M0 |
|
|
|
|
|
|
∂y |
|
M |
0 |
|
|
|
|
|
∂z |
|
M0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
grad u |
|
22 + (− 2)2 |
+ 22 |
|
= |
|
|
= 2 |
|
|
|
. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
ленный вопрос, вычисляем |
|
|
12 |
3 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Теорема 1.9 Для функции двух переменных u = u(x, y) |
вектор grad u на- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
правлен |
перпендикулярно |
к |
касательной, |
проведенной |
к |
линии |
|
уровня |
||||||||||||||||||||||||||||||||||||||||||||||||||||
u(x, y) = c в точке M(x, y) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
Теорема 1.10 Градиент функции трех переменных u = u(x, y, z) направлен |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
по нормали к поверхности уровня, проходящей через данную точку. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Доказательство этих двух теорем вытекает непосредственно из результатов |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
десятого параграфа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
ПРИМЕР |
1.25 |
Определить градиент |
функции |
u = |
x2 |
+ |
y2 |
|
в точке |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|||
M 0 (2;4)
39
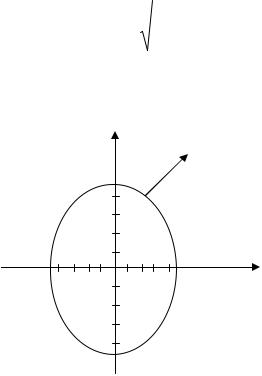
Решение. Уравнение линии уровня, проходящей через точку M 0 имеет вид:
|
x2 |
+ |
y2 |
= |
22 |
|
|
+ |
42 |
= |
12 + 32 |
= |
|
44 |
= |
|
|
22 |
; |
|
x2 |
+ |
|
|
y2 |
|
|
= |
|
22 |
|
|
. Вычисляем коор- |
||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
3 |
2 |
|
|
3 |
|
6 |
|
|
6 |
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
||||||||||||||||||||||||||
динаты вектора grad u в точке M 0 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
∂u = |
2x |
= x; |
|
∂u = |
2y |
; |
|
|
∂u |
|
|
= 2; |
|
∂u |
|
|
|
= |
8 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
∂x 2 |
|
|
|
|
|
∂y 3 |
|
|
∂x |
|
M0 |
|
|
|
∂y |
|
M |
3 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
grad u |
|
|
|
= 2; |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
M |
0 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
длина этого вектора равна |
|
grad u |
|
= |
4 + |
64 |
|
= |
= 3 |
1 |
|
. На рис. 1.9 век- |
|||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
тор grad u изображен в соответствии с заданным масштабом.
y
M 0
1 |
x |
Рис. 1.9
40
