Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Нефтяной Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5_УМК

.PDF

Скачиваний:

Добавлен:

17.03.2015

Размер:

1.51 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1413 14 > Следующая >>>

2. Пусть y = f(x) −		полином	2-й степени, т.е. y = f(x, a 0 , a1 , a 2 ) =
= a 0 + a1 x + a 2 x2	− график этой функции есть парабола. В этом случае вспомо-
гательная функция	Φ = Φ(a 0 , a1 , a 2 )		есть функция трех переменных и имеет
вид:			+ a1xi + a 2 xi2 ))2
Φ = Φ(a 0 , a1 , a 2 ) =		n
		∑ (yi − (a 0		(3.4.8)
		i=1

Тогда система (3.4.3) будет представлена тремя уравнениями:

	∂Ф		n
	∂Ф	= 2∑ (yi			− (a 0	+ a1 x i + a 2 x i2
	∂а0	= 2∑ (yi			− (a 0	+ a1 x i + a 2 x i2
	∂а0		i=1				2
∂Ф			n				2
		= 2∑ (yi			− (a 0	+ a1 x i + a 2 x i
	∂а1	= 2∑ (yi			− (a 0	+ a1 x i + a 2 x i
	∂а1		i=1
	∂Ф		n				2
		= 2∑ (yi			− (a 0	+ a1 x i + a	2 x i
	∂a 2	= 2∑ (yi			− (a 0	+ a1 x i + a	2 x i
	∂a 2		i=1
∑ (y − (a + a x + a x 2 ))= 0
	n
		i		0	1 i	2 i

i=n1	(yi − (a 0 + a1xi + a 2 xi2 )) xi = 0
∑	(yi − (a 0 + a1xi + a 2 xi2 )) xi = 0
i=1
∑n	(yi − (a 0 + a1xi + a 2 x i2 )) xi2 = 0
i=1

)) (−1) = 0

)) (−x i )) = 0

)) ((−x i2 ) = 0

∑ yi		− ∑ a 0 − a1		∑ x i − a	2	∑ x i2	= 0
	n	n		n		n
i=1		i=1		i=1		i=1
	n	x i	n	n			n
	∑ yi	x i	− a 0 ∑ x i − a1 ∑ x i2 − a 2 ∑ x i3					= 0 (3.4.9)
i=1			i=1	i=1			i=1
	n	x i2	n	n			n
∑ yi		x i2	− a 0 ∑ x i2 − a1 ∑ x i3 − a 2 ∑ x i4					= 0
i=1			i=1	i=1			i=1

Теперь необходимо вычислить коэффициенты этой системы (значения xi и yi даны в таблице (3.4.1)):

n	n		n	n
A1 = ∑ xi	A 2 = ∑ xi2		A 3 = ∑ xi3	A 4 = ∑ xi4
i=1	i=1		i=1	i=1
n	n	xi	n	xi2
B1 = ∑ yi	B2 = ∑ yi	xi	B3 = ∑ yi	xi2
i=1	i=1		i=1

С использованием этих чисел система (3.4.9) принимает вид:

na	0 + A1a1 + A 2 a 2		= B1
		+ A 2 a1 + A3a 2	= B2 (3.4.10)
A1a	0
		+ A3a1 + A 4 a 2 = B3
A 2 a 0

121

Эта система из трех линейных уравнений с тремя неизвестными a 0 , a1 , a 2 . Решим систему по формулам Крамера:

n A1

A 2

;

A 2

A 4

;

A 2

a1 =

;

a 2

A 2

A 4

A 2

Если ≠ 0, то система (3.4.10) имеет единственное решение:

a 0 = a0 ; a1 = a1 ; a 2 = a 2 .

При найденных значениях a 0 , a1 , a 2 функция (3.4.8) имеет минимальное значение. Это доказывается с использованием достаточных условий экстремума функции нескольких переменных (теорема 1.8).

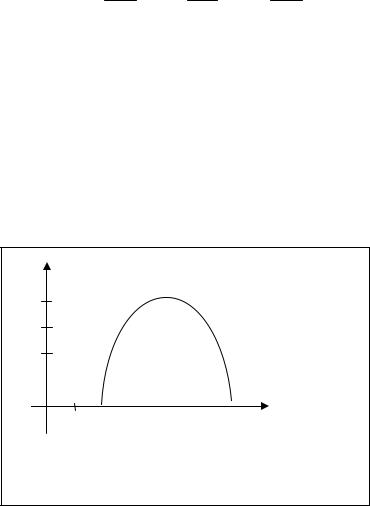
ПРИМЕР 3.4.2. В результате эксперимента получены числовые данные, записанные в виде таблицы 3.4.3:

Таблица 3.4.3

х	2	3	4	5	6
y	0,2	3,0	4,2	2,8	0,5

y
4	•
4

••

1		•				•
1

0							x
0	1	2	3	4	5	6	x

				Рис. 3.4.2

Нанесем эти данные на координатную плоскость, исследуем расположение точек и видим, что зависимость величины y от величины x можно описать пара-

болой, т.е. y = a 0	+ a1 x + a 2 x2 .	Строим	вспомогательную функцию:
5	(yi − (a 0 + a1xi	+ a 2 xi2 ))2
Φ = Φ(a 0 , a1 , a 2 ) = ∑	(yi − (a 0 + a1xi	+ a 2 xi2 ))2	и тогда система (3.4.9) имеет
i=1
вид:

122

∑ yi −		∑
	5	5
i=1		i=1
	5	−
	∑ yi xi	−
i=1
	5
∑ yi xi2		−
i=1

	5		5
a 0 − a1 ∑ xi2		− a 2	∑ xi2	= 0
5	i=1	5	i=1	5
5		5		5
a 0 ∑ xi	− a1 ∑ xi2		− a 2 ∑ xi3
i=1		i=1		i=1
5		5		5
a 0 ∑ xi2	− a1 ∑ xi3		− a 2 ∑ xi4
i=1		i=1		i=1

=0 (3.4.11)

Теперь необходимо вычислить коэффициенты этой системы:

			5
		A1 = ∑ xi		= 2 + 3 + 4 + 5 + 6 = 20
			i=1
		5
A 2 = ∑ xi2			= 22	+ 32 + 42 + 52 + 62 = 4 + 9 + 16 + 25 + 36 = 90
		i=1
		5
A 3	=	∑ xi3	= 23	+ 33	+ 43	+ 53	+ 63	= 8 + 27 + 64 + 125 + 216 = 440
		i=1
		5
A 4	= ∑ xi4		= 24	+ 34	+ 44	+ 54	+ 64	= 16 + 81 + 256 + 625 + 1296 = 2274
		i=1
		5
B1	=	∑ yi	= 0,2	+ 3 + 4,2 + 2,8 + 0,5 = 10,7
		i=1
		5
B2	= ∑ yi xi = 0,2 2 + 3 3 + 4,2 4 + 2,8 5 + 0,5 6 =
		i=1
= 0,4 + 9 + 16,8 + 14 + 3 = 43,2

3= ∑ yi x2i = 0,2 22 + 3 32 + 4,2 42 + 2,8 52 + 0,5 62 =

i=1

=0,2 4 + 3 9 + 4,2 16 + 2,8 25 + 0,5 36 = 0,8 + 27 + 67,2 + 70 + 18 = 183

Подставим полученные значения в систему (3.4.11) или в систему (3.4.10):

5a	0	+ 20a1 + 90a 2 = 10,7
	0 + 90a1 + 440a 2 = 43,2
20a
		+ 440a1 + 2274a 2 = 183
90a 0

Решаем эту систему линейных уравнений методом Крамера:


		5		20	90				10,7		20	90
	=	20		90	440	= 700;		a0 =	43,2		90	440		= −7574;
		90		440	2274				183		940	2275
a1 =			5	10,7	90	= 5148;		a 2 =		5	20	10,7	= −640.
			5	10,7	90					5	20	10,7
			20	43,2	440					20	90	43,2
			90	183	2274					90	440	183
a 0	= − 7574 = −10,82; a1 =						5148	= 7,35; a 2 = − 640 = −0,91.
a 0	= − 7574 = −10,82; a1 =							= 7,35; a 2 = − 640 = −0,91.
	700					700					700

В результате получаем функцию f (x) = −0,91x 2 + 7,35x −10,82 .

123

Для анализа полученного уравнения составим таблицу 3.4.4 Таблица 3.4.4

xi	yi	f(xi )	yi − f(xi )	(yi − f(xi ))	2
xi	yi

2	0,2	0,24	- 0,04	0,0016
3	3,0	3,04	- 0,04	0,0016
4	4,2	4,02	0,18	0,0324
5	2,8	3,18	- 0,02	0,0002

Минимальное значение функции Φ при найденных коэффициентах равно:

Φ = ∑ (yi − f (x i ))2 =0,0016 + 0,0016 + 0,0324 + 0,1444 + 0,0002 = 0,1801.

i=1

Если коэффициенты a 0 , a1 , a 2 хотя бы немного изменить,			то	значение
функции Φ будет увеличиваться.
3. Пусть	y = f(x) −	экспоненциальная функция,	а	именно

y = f(x, b0 , b1 ) = b0 eb1x . В этом случае, при решении системы (3.4.3), возни-

кают трудности, которые, однако, можно преодолеть линеаризацией уравнения y = b0 eb1x . Логарифмируем его: ln y = ln b0 + b1 x; y > 0; b0 > 0. Обозначим

z = ln y; a 0 = ln b0 ; a1 = b1 , тогда имеем z = z(x, a 0 , a1 ) = = a 0 + a1 x − это линейное уравнение. Если найдем его коэффициенты, то исходные коэффициенты

рассчитаем по формулам b0		= ea 0 ; b1 = a1 .
ПРИМЕР 3.4.3. В результате эксперимента получены данные, выписанные в
виде таблицы 3.4.5:
			Таблица 3.4.5
	xi	- 1	0	1	2	3
	yi	6	2	7/9	1/3	1/10

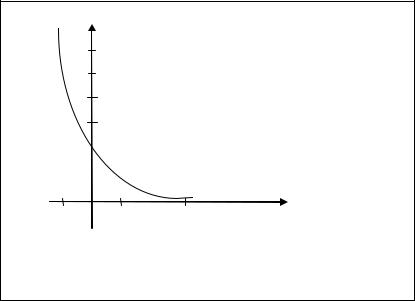
Нанесем эти данные на координатную плоскость (рис.3.4.3), исследуем расположение точек и видим, что лучше всего зависимость

124

• 6

	•
1		•	•	•
1		•

−1 0						x
−1 0		1	2	3	4	x

				Рис. 3.4.3

величины y от величины x описывается экспоненциальной функцией:

y = b0 e b1x . Поскольку в данном случае y > 0; b0

> 0,

то прологарифмируем

уравнение: ln y = ln b0 + b1 x , сделаем обозначения z = ln y ;

a 0

= ln b0 ; a1 = b1 и получаем линейное уравнение z = a 0

+ a1 x . (3.4.12)

Для нахождения коэффициентов у последнего уравнения, воспользуемся

изложенной выше теорией и обратимся к примеру 3.4.1.

Таблица 3.5.6

- 1

7/9

1/3

1/10

ln 6 = 1,792

ln 2 = 0,693

= −0,251

= −1,1

= −2,303

− (a 0

+ a1 xi ))2

Строим вспомогательную функцию Φ = Φ(a 0 , a1 ) = ∑ (zi

. Сис-

i=1

тема (3.4.5) имеет вид в этом случае:

∑ zi

− ∑ a

− a1

∑ xi = 0

5a 0

+ A1a1 = B1

(3.4.13)

i5=1

i=1

0 + A 2 a1 = B2

∑ x

− a

∑ x

− a

∑ x

= 0

A1 a

i=1

1 i=1

Вычислим коэффициенты A1 , A 2 , B1 , B2 :

A1 = ∑ xi

= −1 + 0

+ 1 + 2 + 3 = 5

i=1

= (− 1)2

A 2 = ∑ xi2

+ 02 + 12 + 22 + 32 = 1 + 0 + 1 + 4 + 9 = 15

i=1

125

= ∑ zi

= 1,792 + 0,693 − 0,251 − 1,1 − 2,303 = −1,169

i=1

(− 0,251) 1 + (− 1,1) 2 + (− 2,303) 3 =

= ∑ zi xi = 1,792 (− 1) + 0,693 0 +

i=1

= −1,729 + 0 − 0,251 − 2,2 − 6,909 = −11,152.

Подставим в систему (3.4.13):

5a 0

+ 5a1 = −1,169

= 75 − 25 = 50

+ 15a1 = −11,152

5a 0

− 1,169

= −17,535 + 55,764 = 38,225

− 11,152 15

− 1,169

= −55,76 + 5,845 = −49,915 ≈ −50

− 11,152

= − 50 = −1.

a 0

38,225

= 0,7645, a1

= ln b0 , то найдем ис-

Возвращаемся к коэффициентам b0

и b1 . Так как a 0

комые коэффициенты: b0

= ea0 = e0,7645

= 2,15; b1 = a1

= −1, а также получим

функцию f(x) = 2,15 e−x .

Для анализа полученного уравнения составим таблицу 3.4.7:

				Таблица 3.4.7
xi	yi	f(xi )	yi − f(xi )	(yi − f (xi ))	2
xi	yi


- 1	6	5,848	0,152	0,023
0	2	2,15	- 0,15	0,0225
1	7 9 ≈ 0,77	0,79	- 0,012	0,000144
2	1 3 ≈ 0,33	0,29	0,039	0,0015
3	1 10 ≈ 0,1	0,107	- 0,007	0,00005
Минимальное значение функции Φ при найденных коэффициентах равно:
Φ = ∑5 (yi	− f (x i ))2 = 0,023 + 0,0225 + 0,000144 + 0,0015 + 0,00005 = 0,0472
i =1

126

Задание к лабораторной работе

В результате эксперимента получены данные, выписанные в виде таблицы. Методом наименьших квадратов требуется установить функциональную зависи-

мость величины y от величины x : y = f(x)
	Вариант	1
	x	1,5	2,5	3,5	4,5	5,5	6,5
	y	0,5	7,5	12,5	14,5	14,5	15
	Вариант	2
	x	-0,5	0,5	1,5	2,5	3,5	4,5
	y	10,5	9,5	6,5	4,5	2,5	2,5
	Вариант	3
	x	2,5	3,5	4,5	5,5	6,5	7,5
	y	0,5	3,5	4,5	4,5	4,5	4
	Вариант	4
	x	0,5	1,5	2,5	3,5	4,5	5,5
	y	0,5	5,5	6,5	8,5	9,5	9
	Вариант	5
	x	-0,5	0,5	1,5	2,5	3,5	4,5
	y	9,5	7,5	5,5	6,5	6,5	6,5
	Вариант	6
	x	3,5	4,5	5,5	6,5	7,5	8,5
	y	0,5	6,5	12,5	14,5	15,5	15
	Вариант	7
	x	-2,5	-1,5	-0,5	0,5	1,5	2,5
	y	0,5	1,5	2,5	2,5	2,5	4
	Вариант	8
	x	0,5	1,5	2,5	3,5	4,5	5,5
	y	10,5	10,5	9,5	9,5	6,5	7,5
	Вариант	9
	x	4,5	5,5	6,5	7,5	8,5	9,5
	y	0,5	3,5	8,5	8,5	9,5	10

127

	Вариант	10
	x	-1,5	-0,5	0,5	1,5	2,5	3,5
	y	9,5	9,5	8,5	7,5	6,5	7,5
	Вариант	11
	x	-1,5	-0,5	0,5	1,5	2,5	3,5
	y	0,5	4,5	5,5	5,5	6,5	8
	Вариант	12
	x	-2,5	-1,5	-0,5	0,5	1,5	2,5
	y	9,5	9,5	9,5	5,5	6,5	8
Вариант		13
	x	1,5	2,5	3,5	4,5	5,5	6,5
	y	0,5	3,5	3,5	3,5	4,5	4
Вариант		14
	x	-1,5	-0,5	0,5	1,5	2,5	3,5
	y	10,5	10,5	10,5	8,5	8,5	11
Вариант		15
	x	1,5	2,5	3,5	4,5	5,5	6,5
	y	0,5	5,5	5,5	7,5	8,5	9
Вариант		16
	x	3,5	4,5	5,5	6,5	7,5	8,5
	y	0,5	8,5	9,5	10,5	10,5	10
Вариант		17
	x	-3,5	-2,5	-1,5	-0,5	0,5	1,5
	y	9,5	7,5	7,5	10,5	11,5	12
Вариант		18
	x	1,5	2,5	3,5	4,5	5,5	6,5
	y	0,5	2,5	3,5	3,5	4,5	4
Вариант		19
	x	-2,5	-1,5	-0,5	0,5	1,5	2,5
	y	0,5	1,5	3,5	3,5	4,5	6
Вариант		20
	x	0,5	1,5	2,5	3,5	4,5	5,5
	y	10,5	10,5	9,5	8,5	6,5	6,5

128

Вариант	21
x	2,5	3,5	4,5		5,5		6,5		7,5
y	0,5	0,5	5,5		7,5		8,5		9
Вариант	22
x	0,5	1,5	2,5		3,5		4,5		5,5
y	9,5	8,5	8,5		6,5		5,5		6,5
Вариант	23
		-
x	-3,5	2,5	-1,5		-0,5		0,5		1,5
y	0,5	7,5	7,5		9,5		10,5		11
Вариант	24
		-
x	-4,5	3,5	-2,5		-1,5		-0,5		0,5
y	8,5	7,5	7,5		7,5		8,5		9
Вариант	25
x	1,5	2,5		3,5		4,5		5,5	6,5
y	0,5	3,5		4,5		6,5		6,5	6
Вариант	26
x	-0,5	0,5		1,5		2,5		3,5	4,5
y	10,5	8,5		6,5		6,5		4,5	5,5
Вариант	27
x	2,5	3,5		4,5		5,5		6,5	7,5
y	0,5	9,5		11,5		12,5		12,5	12
Вариант	28
x	4,5	5,5		6,5		7,5		8,5	9,5
y	0,5	9,5		15,5		17,5		18,5	18
Вариант	29
x	-0,5	0,5		1,5		2,5		3,5	4,5
y	9,5	7,5		6,5		8,5		10,5	8,5
Вариант	30
x	4,5	5,5		6,5		7,5		8,5	9,5
y	0,5	0,5		1,5		3,5		3,5	3

129

СПИСОК ЛИТЕРАТУРЫ

Основная литература:

1.Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. - М., Наука, 1988.

2.Пискунов Н.С. Дифференциальные и интегральные исчисления. Т.1,2. - М.,

Наука, 1985.

3.Берман Г.Н. Сборник задач по курсу математического анализа. – М., Наука, 1985.

Дополнительная литература:

1.Шипачев В.С. Курс высшей математики. (Анализ функций нескольких переменных. Ряды. Дифференциальные уравнения) – М., Изд-во МГУ, 1982. - 328 с.

2.Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях

изадачах. – М., Высшая школа, 2000.

3.Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей математики. –

М.: Высшая школа, 1978. – т.2. - 328 с.

4.Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Нау-

ка, 1986. - 576 с.

Учебные пособия кафедры:

1.Функции нескольких переменных/Р.Г. Гимаев, Т.В. Умергалина. – Уфа: Изд-во УГНТУ, 2005.

2.Практикум. Дифференциальное исчисление функций нескольких переменных/Э.В. Галиакбарова, Д.К. Хакимов. – Уфа: Изд-во УГНТУ, 2000.

3.Расчетные задания по теории функций нескольких переменных/ Э.В. Галиакбарова, Р.А. Егорова, Д.Ф. Якубова. – Уфа: Изд-во УГНТУ, 2004.

130

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1413 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.12.2018882.18 Кб2653-70 .doc
#
23.11.2018308.74 Кб36546574645.doc
#
05.12.2018367.62 Кб14589844.doc
#
17.03.2015180.12 Кб505kursovoy_proekt.docx
#
22.08.20194 Mб65_PZ_-_3__38_listy (1).docx
#
17.03.20151.51 Mб345_УМК.PDF
#
06.03.201623.67 Кб55модуль.doc.docx
#
03.09.201947.57 Кб106 БЕЗОПАСНОСТЬ И ЭКОЛОГИЧНОСТЬ ПРОЕКТА+++++.doc...docx
#
18.12.2018387.58 Кб216-10, 21-25, 36-40, 50-53.doc
#
25.09.201993.14 Кб36-10.docx
#
19.11.2018108.54 Кб26. Основы методики самостоят. зан. физ. упр..doc