−
Итак, уравнение Шредингера приводит к тому, что каждое квантовое состояние электрона в атоме водорода характеризуется набором квантовых чисел n, l, m, которым соответствует определенная энергия электрона, момент импульса и его проекция на выделенное направление. Подсчитаем число возможных состояний электрона с данным квантовым числом n. Так как m принима-
ет (2l + 1) значение, а l может изменяться от 0 |
до n – 1, то полное число со- |
|||
стояний равно |
1+[2(n −1)+1] |
|
|
|
n∑−1(2l +1)= |
n = n2 . |
(6.3.10) |
||
2 |
||||
l=0 |
|
|
||
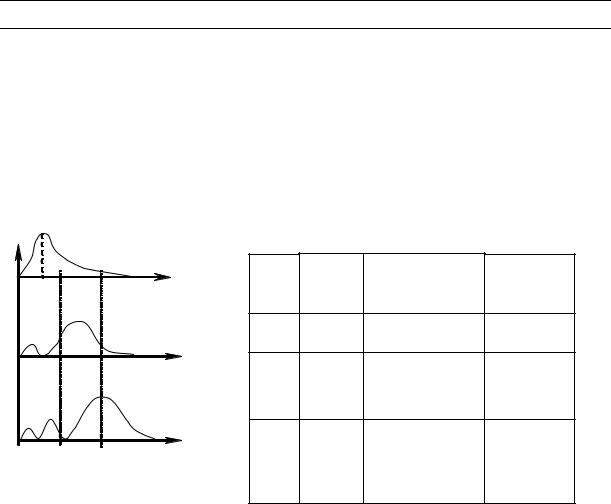
Ниже приведены возможные состояния электронов в атоме. Если теория Бора допускала наглядное представление состояния электрона в атоме с помощью орбит, то квантовая теория вообще не допускает существование орбит.
Решение уравнение Шредингера позволяет находить |ψ|2 = W |
- вероят- |
ность нахождения электрона внутри заданного объема. На рис. 33.2 |
показаны |
распределения вероятности для различных состояний электрона. Так, для основного состояния электрона 1S вероятность W(r) имеет максимум на расстоянии первой боровской орбиты. Таким образом, боровские орбиты электрона в атоме представляют собой геометрические места точек, в которых с наибольшей вероятностью может быть обнаружен электрон.
6.4.МНОГОЭЛЕКТРОННЫЕ АТОМЫ
6.4.1.Спин электрона
Еще до создания квантовой механики было установлено, что детальную структуру спектра излучения атома можно объяснить, если принять, что электрон помимо энергии, связанной с его орбитальным движением, обладает дополнительной энергией. Естественно было допустить, что электрон вращается вокруг своей оси (такое вращение называется спином), чем и обусловлена эта дополнительная энергия. Если приписать электрону собственный момент им-
W(r) |
1S |
r |
n |
l |
обозначение |
m |
|
|
|
||||||
r1 1 |
2 |
A0 |
|
|
состояния |
|
|
1 |
0 |
1S |
0 |
||||
|
|
r |
|||||
|
|
|
|
|
|
||
1 |
2 |
A0 |
2 |
0 |
2S |
0 |
|
|
|
|
|
1 |
2p |
-1, 0, 1 |
|
|
|
r |
3 |
0 |
3S |
0 |
|
1 |
2 |
A0 |
|||||
|
1 |
3p |
-1,0,1 |
||||
Рис. 6.3.2 |
|
|
2 |
3d |
-2,-1,0,1,2 |
||
|
|
|
|
|
|||
−
пульса LS (часто эту величину называют просто спином), то из общих выводов квантовой механики следует, что спин должен быть квантован по закону
LS = S(S +1)h, |
(6.4.1) |
где S – спиновое квантовое число. |
|
Аналогично результату (6.3.9) |
проекция LSZ также должна квантоваться |
по закону |
|
LSZ = mSh, |
(6.4.2) |
принимая при этом (2S + 1) |
различные ориентации. Проведенные в |
1921 г. О. Штерном и В. Герлахом опыты по определению магнитных моментов атомов, во-первых, подтвердили пространственное квантование магнитных и связанных с ними механических моментов атомов, а во-вторых, установили,
что для |
спина |
электрона |
число возможных ориентаций всего |
2, так что |
||||
2S + 1 = 2, т.е. |
S = ½. Численное значение спина равно |
|
||||||
LS |
= |
1 |
|
1 |
|
3 |
(6.4.3) |
|
2 |
|
2 |
+1 h = |
2 |
h, |
|||
|
|
|
|
|
|
|||
а число m |
может принимать лишь два значения: |
m |
S |
= ± 1 |
. Это число |
S |
|
|
2 |
|
|
|
|
|
|
|
можно было бы назвать магнитным спиновым числом, но это название не при-
меняется. Говоря о спиновом квантовом числе, понимают под ним |
mS. Таким |
||
образом, проекция спинового момента может принимать два значения: |
|||
LSZ = ± |
1 |
h. |
(6.4.4) |
|
|||
2 |
|
|
|
Еще раз уточним, что представление о спине, связанное с вращением электрона вокруг оси, является неверным. Спин электрона как и других частиц рассматривают как их особое свойство, подобно массе и заряду.
Итак, с учетом спина электрона его состояния в атоме характеризуется набором четырех квантовых числе: n, l, m, mS (или просто спинового числа S).
6.4.2. Принцип Паули
В 1925 г. В. Паули установил квантовомеханический закон, называемый принципом Паули: в одном квантовом состоянии, определяемом набором кван-
товых чисел n, l, m, mS, не может находиться более одного электрона.
Тогда максимальное число электронов, находящихся в состояниях, определяемых главным квантовым числом n, равно 2n2. Электроны в атоме, занимающие состояния с одинаковым n, образуют электронную оболочку или слой. Различают следующие оболочки К, при n = 1, L, при n = 2 и т.д. В каждой оболочке электроны распределяются по подоболочкам – состоянием с одинаковым l . В таблице приведены максимальные числа электронов, находящихся в оболочках и подоболочках.
n |
оболочка |
количество электронов |
|
|
максимальное |
||
S |
p |
d |
f |
g |
число |
||
|
|
|
|
|
− |
|
|
|
|
|
l=0 |
l=1 |
l=2 |
|
l=3 |
l=4 |
|
|
|
электронов |
||||||
1 |
К |
2 |
- |
- |
|
- |
- |
2 |
2 |
L |
2 |
6 |
- |
|
- |
- |
8 |
3 |
M |
2 |
6 |
10 |
|
- |
- |
18 |
4 |
N |
2 |
6 |
10 |
|
14 |
- |
32 |
5 |
0 |
2 |
6 |
10 |
|
14 |
18 |
50 |
6.4.3. Электронная структура оболочек атомов
На основании закономерностей в строении атомов объясняется строение периодической системы элементов Менделеева. Заполнение электронами оболочек производится в соответствии с принципом Паули и требованием минимальной энергии электрона в данном состоянии.
Из этих принципом можно установить связь между распределением электронов в атоме по энергетическим состояниям и положениям атома в периодической системе. Так, у атома водорода один электрон находится на К-оболочке, занимая S состояние, что принято обозначать 1S1. У атома гелия два электрона в этом же состоянии, но отличаются направлением спина, что принято обозначать 1S2. У следующего атома лития начинает застраиваться L-оболочка. Его конфигурация 1S22S1 и т.д. Такая последовательность заполнения электронных слоев наблюдается вплоть до восемнадцатого элемента аргона, имеющего конфигурацию
1S22S22p63S23p6.
Девятнадцатый электрон калия должен был бы занять состояние 3d в m- оболочке. Однако химические его свойства аналогичны свойствам лития и натрия, у которых валентный электрон находится в S-состоянии. У калия этот электрон занимает 4S состояние, т.е. при незаполненной М-оболочке начинает застраиваться N-оболочка. Такие отступления наблюдаются и у других элементов, что объясняется соблюдением принципа минимальной энергии электрона в соответствующем состоянии.
6.4.4. |
Рентгеновские лучи |
|
|
|
В изучении строения электронных оболочек большую |
- |
|||
роль сыграли рентгеновские лучи, открытые В.К. Рентгеном в |
|
|||
1895 г. Эти лучи возникают при прямом взаимодействии ле- |
|
|||
тящих с |
катода электронов с атомами |
материала |
анода |
|
(рис. 6.4.1). Для их получения используются специальные |
|
|||
рентгеновские трубки, в которых между катодом и анодом |
|
|||
создается напряжение порядка 10-100 кВ. Рентгеновские лучи |
|
|||
представляют собой короткие электромагнитные волны с дли- |
+ |
|||
|
0 |
|
|
|
ной волны от 0,01 А. Волновая электромагнит- |
θ D |
Рис. 6.4.1 |
||
ная природа этих лучей была доказана опытами |
||||
по дифракции электронов на кристаллах, проде- |
|
|
||
ланных М. Лауэ с сотрудниками в 1912 г. |
Кри- d |
A |
C |
|
сталл, состоящий из упорядоченно расположен-
B
Рис. 6.4.2
−
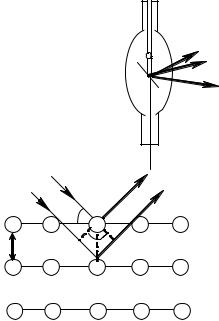
ных частиц, представляет собой пространственную дифракционную решетку. Дифракцию рентгеновских лучей можно рассматривать как результат их отражения от системы параллельных атомных плоскостей (рис. 6.4.2). Для того чтобы лучи, отраженные от соседних плоскостей, усиливали друг друга, необходимо, чтобы разность хода между ними была равна целому числу волн (интерференционные максимумы), т.е.
= AB + BC = 2dsinθ = kλ.
Следовательно, максимумы интенсивностей дифрагированных лучей будут
наблюдаться для углов, удовлетворяющих условию |
|
2d sin θ = kλ. |
(6.4.5) |
Эта формула называется формулой Вульфа-Брэгга.
Существует две разновидности рентгеновских лучей, причины возникновения которых совершенно различны. Одна из компонент представляет собой тормозное излучение, имеющее непрерывный спектр.
Возникновение этого излучения можно объяснить так. Вокруг движущегося электрона существует магнитное поле. При ударе об анод происходит резкое изменение скорости электрона и соответственно магнитного поля, в результате чего возникают электромагнитные волны. Сплошной спектр такого излучения объясняется тем, что различные электроны по разному тормозятся атомами анода, что и приводит к излучению различных волн. Согласно квантовой теории часть кинетической энергии электрона переходит при соударении в тепло
W, остальная часть в энергию фотона рентгеновского излучения: |
|
|||
|
mV2 |
|
|
|
hν = |
0 |
− W |
|
|
2 |
(6.4.6) |
|||
|
. |
|||
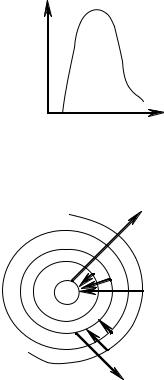
Таким образом, формальной точки зрения возникновение тормозного рентгеновского излучения обратно внешнему фотоэффекту. Отсюда можно получить коротковолновую границу рентгеновского спектра (рис. 6.4.3). При
|
|
|
|
|
|
|
mV |
2 |
|
ν = νmax , |
W = 0 |
и hνmax = |
0 |
= eU |
|||||
|
|||||||||
|
|
|
|
|
|
|
2 |
|
, |
где U – приложенная разность потенциалов. То- |
|||||||||
гда |
|
|
|
|
|
|
|
|
|
λmin = |
c |
|
= |
hc |
|
|
|
|
|
νmax |
eU |
. |
|
0 |
|
(6.4.7) |
|||
Так, для U = 50 B, |
λmin = 0,23 A . |
|
|
||||||
Малая длина волны рентгеновских лучей является причиной их большой проникающей способности, химического, ионизирующего действия, а также опасного биологического воздействия. На непрерывный спектр тормозного излучения накладывается другая компонента – характеристическое рентгеновское излучение. Свое название оно полу-
интенсивность |
λ |
|
|
|
Рис. 34.3 |
|
К-серия |
К
L
M N
L-серия
Рис. 6.4.4