−
3.8.5.Магнитное поле проводника с током. Закон Био-Савара-Лапласа
Если по проводнику течет ток, то вокруг него возникает магнитное поле. Индукцию такого поля можно определить, исходя из формулы (3.8.6). Для этого введем понятие элемента тока. Элемент тока определяется как произведе-
ние силы тока в проводнике i на элемент длины проводника |
l. Элемент тока |
||||
i = i l = |
q l |
= |
q V . |
(3.8.10) |
|
t |
|||||
|
|
|
|
||
Как видно, движущийся заряд q математически эквивалентен элементу тока. Направление тока совпадает с направлением тока в проводнике. Поэтому и силы, действующие на токи, не что иное, как силы, действующие между движущимися зарядами. Поставим (3.8.10) в (3.8.6):
B = μ0i lsin α . |
|
(3.8.11) |
4πr2 |
|
|
Эта формула определяет индукцию магнитного поля, созданного элемен- |
||
том тока на расстоянии r от него (рис. 3.8.5). Она выражает |
l |
i |
закон Био-Савара-Лапласа. С его помощью можно вычислять |
|
|
индукцию магнитных полей, созданных токами различной |
|
α r |
конфигурации. Для удобства вычислений (18.11) записыва- |
|
|
ют в дифференциальной форме: |
|
|
||
dB = |
μ0i dlsin α |
(3.8.12) |
|
|
|
4πr2 |
|
|
B |
или в векторном виде |
|
|
||
dB = |
μ0i [dl r] |
. |
(3.8.13) |
Рис. 3.8.5 |
4πr3 |
|
|||
Если магнитное поле создано несколькими токами, то результирующее поле находят как векторную сумму отдельных полей. Таким образом, как и для электрического поля, так и для магнитного поля справедлив принцип суперпозиции:
B = B1 + B2 +... = ∑Bi . |
(3.8.14) |
3.9.МАГНИТНОЕ ПОЛЕ ПРОВОДНИКОВ С ТОКОМ
3.9.1. Магнитное поле токов
Пользуясь законом Био-Савара-Лапласа, найдем индукцию магнитного поля в точке А (рис. 3.9.1) на расстоянии х от оси провода, длина которого значительно больше х. Индукция элемента проводника dl определяется формулой (3.8.12). Как видно из рис. 3.9.1
dlsin α |
= |
dlcosβ |
= |
dS |
= dβ; |
r = |
x |
. |
|
r |
r |
r |
cosβ |
||||||
|
|
|
|
|
Подставив эти выражения в (3.8.12), находим
dl |
dS |
|
|
|
|
||
α r |
β |
dβ |
|
x |
A |
||
|
|||
|
|
||
i |
B |
|
|
Рис. 3.9.1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
dB = |
|
μ0i dlsin α |
= |
μ0icosβ dβ . |
|
|
|
|
|||||||||||
|
|
|
|
4πr2 |
|
|
4πx |
|
|
|
|
||||||||
Полная индукция магнитного поля |
|
|
|
|
|||||||||||||||
|
|
|
μoi |
|
+π/ 2 |
|
|
|
|
|
μ0i |
|
|
|
|
|
|||
B = |
|
|
|
∫ cosβdβ = |
|
|
(3.9.1) |
|
|
|
|||||||||
4πx |
|
|
2πx |
|
|
|
|||||||||||||
|
|
−π/ 2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вычислим теперь индукцию магнитного кругового тока |
|
(рис. 3.9.2). В |
|||||||||||||||||
этом случае все элементы проводника |
dl перпендикулярны радиусу-вектору |
||||||||||||||||||
R и поэтому sin = 1. |
Формула (3.8.12) |
для этого случая имеет вид |
|
||||||||||||||||
dB = |
|
μ0i dl |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
4πR2 |
|
|
|
|
|
|
|
|
i |
R |
dl |
||||
Все элементы |
dl |
создают магнитное поле одного на- |
|||||||||||||||||
правления в центре витка: |
|
|
|
|
|
|
B |
||||||||||||
|
|
|
|
|
|
|
|||||||||||||
B = |
|
|
|
μ0i |
|
∫dl = |
|
|
μ0i |
|
2πR = μ0i . |
(3.9.2) |
|
|
|
||||
|
4πR2 |
|
4πR2 |
Рис. 3.9.2 |
|||||||||||||||
|
|
|
|
|
|
|
2R |
|
|||||||||||
Индукция поля вдоль оси будет уменьшаться по мере |
|
||||||||||
удаления от центра. На некотором расстоянии x |
от центра формула для индук- |
||||||||||
ции поля имеет вид |
|
|
|
|
|
|
|
||||
B = |
μ |
0 |
2πR2i |
= |
μ |
0 |
2iS |
.(3.9.3) |
Pm |
||
|
(R2 + x2 )3/ 2 |
|
(R2 + x2 )3/ 2 |
|
|||||||
|
4π |
|
4π |
|
|
n |
|||||
В случае кругового тока индукция определяется не только |
|||||||||||
|
|||||||||||
током, а произведением тока на площадь витка S. Величину |
|
||||||||||
Pm = i S |
|
|
|
|
|
(19.4) |
Рис. 3.9.3 |
||||
называют магнитным моментом контура. |
Эта величина |
||||||||||
векторная. Направление Pm |
совпадает с направлением внешней нормали и |
||||||||||
плоскости витка (рис. 19.3) |
|
|
|
|
|
||||||
Pm = i S n. |
|
|
|
|
(19.5) |
|
|||||
3.9.2. |
Действие магнитного поля на |
проводники с |
током |
||||||||
Как говорилось, на движущийся электрический заряд в магнитном поле действует сила Лоренца. Т.к. ток в проводнике есть совокупность движущихся зарядов, то на отрезок проводника l будет действовать сила. Заменяя в фор-
мулах (3.8.8) |
и (3.8.9) qV элементом тока i l, |
получаем силу, действующую |
||
на проводник |
l с током в магнитном поле |
|
|
|
F = i [ |
l B] |
|
(3.9.6) |
|
или |
|
|
|
|
F = i l Bsin α. |
|
(3.9.7) |
||
Эти формулы выражают закон Ампера. |
Направление этой силы определя- |
|||
ется как и направление силы Лоренца. |
В |
находится контур с током |
||
Если в |
магнитном поле с индукцией |
|||
(рис. 3.9.4), |
то на каждую его сторону будет действовать сила Ампера. Силы, |
|||
−
действующие на стороны а, перпендикулярны к ним и к полю, поэтому они
направлены вертикально и лишь деформируют контур. Стороны b |
перпенди- |
кулярны к В и на каждое из них действует сила Ампера F = i b B |
(sin α =1) . |
Эти силы стремятся повернуть виток так, чтобы его плоскость была перпендикулярна В. В результате появляется пара сил, момент которой равен
M = Fd = Fasin ϕ = i b B asin ϕ, |
|
|
|
|
||
где d = a sin ϕ - плечо пары. Т.к. b a = S, a i S = Pm, |
то |
|||||
M = PmBsin ϕ |
(3.9.8) |
|||||
или в векторной форме |
|
|
|
|
||
M = [Pm B], |
(3.9.9) |
|||||
т.е. в однородном магнитном поле на контур с током действует вращаю- |
||||||
щийся момент, пропорциональный магнитному |
|
|
|
|
||
моменту контура и индукции поля. Его максималь- |
|
|
|
|
||
|
|
|
|
|||
ное значение Mmax при ϕ = π/2. Из формулы |
|
|
|
|
|
B |
|
|
|
||||
(3.9.8) можно определить индукцию магнитного |
|
|
n |
|||
поля как отношение вращательного момента, дей- |
b |
|
|
|
|
||||
ствующего в магнитном поле, на контур к магнит- |
|
|
|
a |
|
||||
ному моменту контура площадью S с током i: |
|
|
|
|
|||||
B = |
Mmax |
. |
(3.9.10) |
|
|
a |
F |
|
|
Pm |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
B |
|
Пользуясь законом Ампера, можно также най- |
|
+ |
|
ϕ |
|||||
|
|
|
|||||||
ти силу взаимодействия |
между параллельными |
F |
|
n |
|
||||
проводниками |
с токами |
(рис. 3.9.5). Индукция |
|
|
|
|
|||
|
|
|
|
|
|||||
магнитного поля, создаваемая проводником 1, там, |
|
Рис. 3.9.4 |
|
||||||
где находится проводник |
2, определяется форму- |
|
|
|
|
|
|||
лой (3.9.1): |
|
|
|
|
|
|
|
||
B |
= μ0i1 . |
|
|
|
|
|
|
||
1 |
|
2πx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вектор индукции В1 |
перпендикулярен проводу |
2, |
поэтому сила, дейст- |
||||||
вующая на проводник 2, равна |
|
|
|
|
|
||||
F = i2B1l = |
μ0i1i2l . |
(3.9.11) |
|
i1 |
|
x |
i2 |
||
|
|
|
2πx |
|
|
|
|
|
|
Такое выражение получится, если вычислять силу, |
|
|
F |
|
|||||
действующую на проводник 1. Обычно вычисляют си- |
|
|
|
||||||
|
|
|
|
||||||
лу, действующую на единицу длины, т.е. f = F l |
|
|
|
B |
|
||||
f = |
|
μ0i1i2 . |
(3.9.12) |
|
|
|
|
||
|
|
|
|
|
|
||||
|
|
2πx |
|
|
|
|
|
Рис. 3.9.5 |
|
На основании этой формулы устанавливается ос- |
|
|
|
||||||
новная единица силы тока в СИ – ампер (А): 1 А – сила неизменяющегося тока, который при прохождении по двум параллельным пря-
молинейным проводникам бесконечной длины и ничтожно малого сечения,
−
расположенным в вакууме на расстоянии 1 м друг от друга, вызвал бы между ними силу, равную μ2π0 = 2 10−7 Н на каждый метр длины.
3.9.3. Магнитный поток
Поток вектора магнитной индукции вводится как и в электростатике для характеристики интенсивности поля. Его определяют как полное число магнитных силовых линий, пронизывающих площадь S, перпендикулярную линиям. Для прямоугольной площадки и однородного поля
Ф = BScos α = BnS. |
|
|
(3.9.13) |
|||
В общем случае для произвольной поверхности |
||||||
Ф= ∫BndS. |
|
|
|
|
|
(3.9.14) |
S |
|
|
|
|
|
|
Единица магнитного потока имеет специальное название. В СИ единица |
||||||
магнитного потока вебер (Вб): |
|
|
||||
1 Вб=1Тл 1м |
2 |
=1 |
В с |
1м |
2 |
=1В с. |
|
м2 |
|
||||
|
|
|
|
|
|
|
Для замкнутой поверхности |
|
|||||
Ф= ∫BndS = 0. |
|
|
|
|
(3.9.15) |
|
S
Формула (3.9.15) выражает теорему Гаусса для магнитного поля. Этот результат есть следствие замкнутости магнитных силовых линий, что существенно отличает свойства магнитного поля от электрического. Физические поля с замкнутыми силовыми линиями называют соленоидальными.
3.9.4. Работа магнитного поля по |
|
B |
||||
|
|
|||||
|
|
перемещению проводника с током |
|
Bn |
||
На проводник с током в магнитном поле дейст- |
|
|||||
|
l |
|||||
вует сила Ампера, под действием которой он пере- |
i |
|||||
Bτ |
||||||
мещается. Вычислим работу, совершаемую такими |
||||||
силами при перемещении проводника. |
|
x |
||||
Пусть отрезок проводника |
l с током переме- |
|
Рис. 3.9.6 |
|||
щается в магнитном поле с индукцией В на рас- |
|
|||||
|
|
|||||
стояние |
х |
(рис. 3.9.6). Вектор |
В можно разло- |
|
|
|
жить на |
BB |
и BB . Т.к. сила Ампера всегда перпендикулярна полю, то состав- |
||||
|
n |
τ |
|
|
|
|
ляющая BτB |
вызывает силу, перпендикулярную перемещению х, и работа |
|||||
этой составляющей будет равна нулю. Поэтому
A = F x = i Bn l x = i Bn x ,
где S – площадь, описываемая при движении проводника. Окончательно |
|
A = i Bn S = i Ф= i(Ф2 −Ф1 ). |
(3.9.16) |
3.9.5. Закон полного тока
−
Поскольку магнитные силовые линии являются замкнутыми, то соотношение между током и вызванным им магнитным полем характеризуют не потоком магнитной индукции, а циркуляцией вектора магнитной индукции вдоль замкнутой кривой. Для простоты рассмотрим магнитное поле бесконечного прямолинейного проводника с током (рис. 3.9.7). Линии магнитной индукции в этом случае являются концен- 2 трическими окружностями, лежащими в плоскости, перпендикулярной току. В этом случае циркуляция
∫Bldl |
равна. |
Т.к. В во всех точках направлен по ка- 1 |
||||
l |
|
|
|
μ0i |
|
|
сательной, то |
α = 0, а B = |
: |
||||
2πr |
||||||
|
|
|
|
|
||
∫ |
Bldl = μ0i |
∫dl = μ0i . |
|
(3.9.17) |
||
L |
2πr |
0 |
|
|
||
|
|
|
|
|||
+ r
B
Рис. 3.9.7
3
4
Рис. 3.9.8
Этот результат справедлив для любого произвольного контура, который охватывает токи. Если внутри контура имеется несколько токов, то
∫Bldl = μ0 ∑ik . |
(3.9.18) |
L |
|
Формулы (3.9.17) и (3.9.18) |
выражают закон полного тока или теорему о |
циркуляции вектора В. |
|
Для магнитного поля циркуляция вектора магнитной индукции вдоль замкнутого контура равна произведению μ0 на алгебраическую сумму токов, охватываемых этим контуром.
Эта теорема выражает один из основных законов магнетизма. Сопоставляя этот результат с условием потенциальности электростатического поля – формула (3.2.2), видно также, что магнитное поле не является потенциальным. Такие поля называют вихревыми.
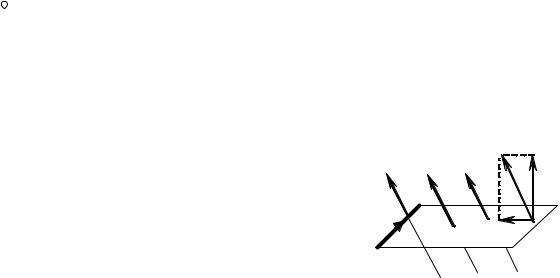
Применим формулу (3.9.17) для вычисления индукции магнитного поля на оси тонкого соленоида – системы круговых токов, диаметр которых много меньше длины (рис. 3.9.8). Индукция внутри такого соленоида направлена
вдоль его оси. применяя (3.9.17) к прямоугольному контуру 1-2-3-4, |
имеем |
||||
|
2 |
3 |
4 |
1 |
|
∫Bldl = ∫Bldl + ∫Bldl + ∫Bldl + ∫Bldl . |
(3.9.19) |
||||
L |
1 |
2 |
3 |
4 |
и 3-4 В |
Т.к. поле сосредоточено внутри соленоида, а на участках 1-2 |
|||||
перпендикулярен участкам контура и Вl = 0, то из (3.9.19) получаем |
|||||
|
1 |
|
|
|
|
∫Bldl = ∫Bldl = Bl = μ0 N i , |
|
||||
L |
2 |
|
|
|
|
где l – длина соленоида, |
N – число витков соленоида. Итак, |
|
|||
B = μ0 |
N |
i = μ0n i . |
|
|
(3.9.20) |
l |
|
|
|||
|
|
|
|
|
|