−
Из этой формулы следует, что дифракционная решетка осуществляет спектральное разложение, т.к. свет с разной длиной волны отклоняется на разные углы. Если решетку освещать белым светом, то все максимумы кроме нулевого становятся окрашенными. Число m называют порядком дифракционного спектра, оно определяет число главных максимумов, которое равно
m ≤ d |
т.к. sin ≤1. |
λ |
|
Как видно, с помощью дифракционной решетки можно измерить длину волны света, для чего надо по заданному d измерить ϕ. Важнейшей характеристикой решетки является ее разрешающая способность, характеризующая свойство решетки разделить (наблюдать раздельно) две близкие длины волны.
Эта величина A = λλ определяется формулой
A = mN, |
(5.2.12) |
|
где m – порядок спектра, N – общее число щелей, λ = (λ1 + λ2 ) |
- длина |
|
волны, вблизи которой ведется измерение, |
λ = (λ1 −λ2 ).. Здесь λ1 |
и λ2 - |
длины волн, которые надо разрешить.
5.3.ПОЛЯРИЗАЦИЯ СВЕТА
5.3.1.Естественный и поляризованный свет
Световая волна, испускаемая источником света, представляет собой наложение цугов электромагнитных волн, испускаемых отдельными атомами светящегося тела. Процесс излу-
чения составляет ~10-8 c. За это время атом испускает обрывок синусоидальной волны длиной l = cτ 3 м, который и на-
зывают цугом волн. Из-за хаотичности излучения отдельных атомов вектора напряженностей Е и Н отдельных цугов ори-
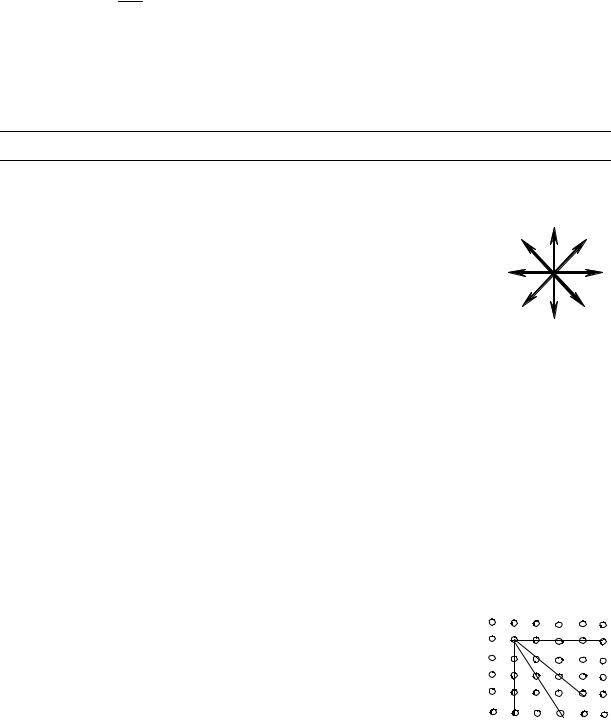
ентированы произвольно. Так что в испускаемом световом луче имеются всевозможные направления этих векторов (рис. 5.3.1). Такой свет называют естественным.
Можно, однако, получить световой луч, в котором вектор Е совершает колебания в заданном направлении. Такой свет называют поляризованным, а процесс его получения – поляризацией. Если световой вектор колеблется вдоль одного направления, то свет называют плоско или линейно-поляризованным, если конец светового вектора описывает эллипс или окружность – то эллиптически или циркулярно поляризованным. Плоскость, в которой колеблется вектор Е, называют плоскостью поляризации.
5.3.2. Поляризация света при прохождении через кристаллы
Если создать условия, при которых векторы Е в луче естественного света могли бы совершать колебания вдоль одного направления, то свет можно поляризовать. Такие ус-
Рис. 5.3.2
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
ловия могут быть созданы при прохождении естественного света через анизо- |
||||||||||||||||
тропную в отношении электрических колебаний среду. Такой средой является |
||||||||||||||||
кристалл, где анизотропия свойств его объясняется наличием кристаллической |
||||||||||||||||
решетки, в которой число частиц, приходящееся на одинаковые по длине, но |
||||||||||||||||
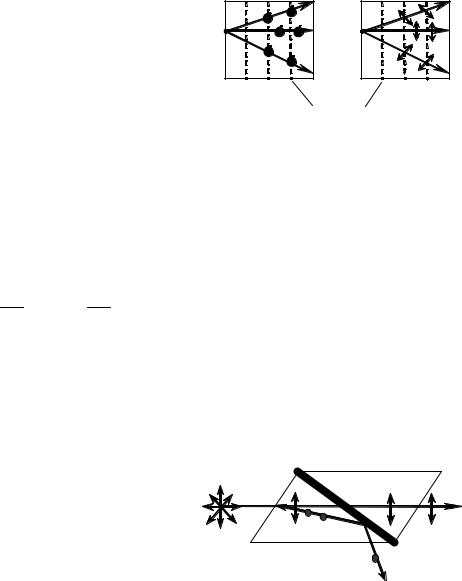
различные по направлению отрезки различное |
(рис. 5.3.2). Переменное элек- |
|||||||||||||||
трическое поле световой волны вызывает переменное смещение атомов и ионов |
||||||||||||||||
решетки, на что затрачивается определенная часть энергии волны. Однако из-за |
||||||||||||||||
различного числа частиц по разным направлениям разные составляющие |
Е |
|||||||||||||||
световой волны теряют различную энергию. |
|
|
|
|
|
|||||||||||
Ясно, что те составляющие Е световой волны, которые распространяются |
||||||||||||||||
в плоскостях, соответствующих большему числу частиц, могут быть полностью |
||||||||||||||||
поглощены кристаллом, и на выходе из него получается поляризованный свет с |
||||||||||||||||
направлением колебаний |
Е, соответствующих минимальному числу частиц в |
|||||||||||||||
решетке кристалла. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
В действительности из-за сложной структуры кристалла процесс поляри- |
||||||||||||||||
зации является более сложным, и из естественного луча образуется не один, а |
||||||||||||||||
два луча, поляризованных во взаимно перпендикулярных плоскостях. Эти лучи |
||||||||||||||||
имеют разные скорости распространения во |
|
|
0 |
|
е |
|||||||||||
всех направлениях, кроме |
одного, |
которое |
|
|
|
|||||||||||
|
|
0 |
|
е |
||||||||||||
называют оптической осью. Один из лучей – |
|
|
|
|||||||||||||
|
|
|
|
|
||||||||||||
обыкновенный |
|
|
(0), |
распространяется во |
|
|
0 |
|
е |
|||||||
всех направлениях с одинаковой скоростью, |
|
|
|
|||||||||||||
|
|
|
|
|
||||||||||||
а колебания его вектора Е всегда перпенди- |
|
|
Главное сечение |
|
||||||||||||
кулярны оптической оси. |
|
|
|
|
|
|
|
|
|
|||||||
Для |
другого – необыкновенного |
луча |
|
|
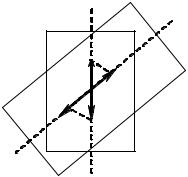
Рис. 5.3.3 |
|
|
|||||||||
Е – колеблется в плоскости главного сечения |
|
|
|
|
|
|||||||||||
кристалла – плоскости, содержащей луч и оптическую ось (рис. 29.3). Описан- |
||||||||||||||||
ное явление называют двойным лучепреломлением. Оно впервые наблюдалось |
||||||||||||||||
на кристалле исландского шпата (кальцит) в 1670 г. Бартолини. Таким свойст- |
||||||||||||||||
вом обладают также кварц, турмалин, лед, слюда и другие кристаллы. |
|
|||||||||||||||
Для обыкновенного и необыкновенного лучей существует свой показатель |
||||||||||||||||
преломления: |
n |
0 |
= c |
; |
n |
e |
= |
c . |
Если V |
0 |
> V , то соответствующий кри- |
|||||
|
|
|
V0 |
|
|
|
Ve |
|
|
|
e |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
сталл называют положительным (кварц), если же V0 < Ve, то кристалл отрица- |
||||||||||||||||
тельный (кальцит). |
|
|
|
|
|
|
|
|
|
|
|
|
||||
5.3.3. |
Получение |
поляризованного |
света |
|
|
|||||||||||
Явление двойного лучепреломления используется для получения поляри- |
||||||||||||||||
зованного света. Наиболее часто для этих целей используют поляризационные |
||||||||||||||||
призмы и поляроиды. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Одной из распространенных поляри- |
|
|
|
|
е |
|||||||||||
зационных призм является призма Николя |
|
|
|
|
||||||||||||
(рис. 5.3.4). Она |
изготавливается |
из |
ис- |
|
|
|
|
|
||||||||
ландского шпата (кальцит). Две трехгран- |
|
|
|
0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.3.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−
ные призмы склеиваются специальным прозрачным веществом – канадским бальзамом с показателем преломления n = 1,549. На передней грани призмы
естественный свет разделяется на обыкновенный, для которого n0 = 1,659, и необыкновенный, для которого ne = 1,515. Углы составных призм выбираются так, чтобы на границе призм обыкновенный луч испытывал полное внутреннее отражение. Т.к. n < n0, то канадский бальзам является для обыкновенного луча средой оптически менее плотной и он, испытывая полное внутреннее отражение, выводится из призмы. Для необыкновенного луча n > ne, поэтому этот луч проходит слой канадского бальзама.
Поляризованный свет получают и с помощью поляроидов – тонкой пленки, содержащей множество легких кристалликов, обладающих свойством оптического дихроизма. Это свойство заключается в том, что кристалл поглощает один из двух лучей, возникающих за счет двойного лучепреломления. Так, например, кристалл турмалина при толщине ~1 мм полностью поглощает обыкновенный луч.
Поляризационные приборы делятся на поляризаторы Р и анализаторы А. Первые служат для получения, а вторые для анализа поляризованного света. Различий между ними нет и их можно менять местами.
5.3.4. Закон Малюса
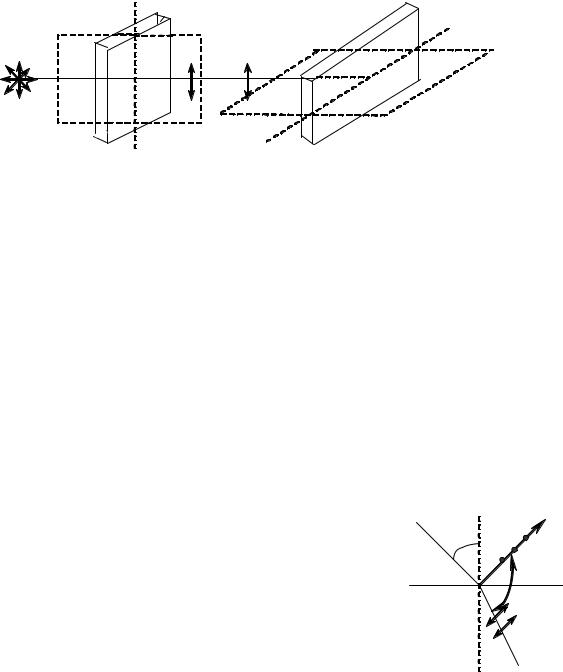
Рассмотрим естественный луч света, прошедший пластинку турмалина с оптической осью 00’. В этом случае свет полностью поляризуется в плоскости,
перпендикулярной главному сечению |
(рис. 5.3.5). |
Если за пластинкой 1 по- |
|||
местить вторую такую же пластинку |
2, но так, что ее оптическая ось перпен- |
||||
дикулярна первой, то через нее луч не пройдет. |
|
|
|||
Если же повернуть вторую пластинку так, что при этом угол |
ϕ между их |
||||
оптическими осями будет отличен от |
900, то часть |
0’ |
|
||
луча пройдет и вторую пластинку. Амплитуда про- |
|
0’ |
|||
шедших |
колебаний при этом |
будет |
равна |
|
ϕ |
(рис. 5.3.6) |
E = E0cos ϕ. Т.к. интенсивность |
I~A2, |
E0 |
E |
|
то |
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
1
0
Рис. 5.3.6
|
|
− |
|
0’ |
|
2 |
0’ |
|
1 |
||
|
|
||
|
|
|
|
0 |
0 |
|
|
|
|
|
Рис. 5.3.5 |
I = I0 cos2 ϕ, |
|
(5.3.1) |
где I0 – интенсивность поляризованного света, падающего на вторую пластинку (анализатор), I – интенсивность света, прошедшего через нее. Формулу (5.3.1) называют законом Малюса.
5.3.5. Поляризация при отражении и преломлении
Опыт показывает, что при падении на диэлектрик (вода, стекло) отраженный и преломленный лучи всегда частично поляризованы. Степень поляризации при этом зависит от угла падения и показателя преломления отражающей среды. При этом отраженный луч частично поляризован в плоскости, перпендикулярной плоскости падения, а преломленный – в плоскости падения. Условие полной поляризации состоит в том, чтобы угол между отраженным и преломленным лучами был равен π/2, т.е., чтобы
n 21 |
= |
n 2 |
= |
sin i0 |
= |
sin i0 |
= tg i0 . |
(5.3.2) |
n1 |
sin r |
|
||||||
|
|
|
|
cos i0 |
|
|||
Это соотношение называют законом Брюстера. Для стекла n = 1,5 и i ≈ 530. Этот закон объясняется тем, что отраженный и преломленный лучи представляют собой вторичное излучение, возбужденное падающей волной. Электроны колеблются в направлении вектора Е (рис. 5.3.7). Однако, электрический диполь не излучает в этом направлении, максимум излучения приходится на перпендикулярное направление.
5.3.6. Вращение плоскости поляризации
i0 n1
n2 
π/2
r Рис. 5.3.7
Некоторые вещества, называемые оптически активными, обладают способностью при пропускании через них линейно поляризованного света поворачивать плоскость поляризации. К ним относятся кварц, растворы оптически активных веществ (раствор сахара и др.).
Кристаллические вещества сильнее всего вращают плоскость поляризации,
если свет распространяется вдоль оптической оси. Угол поворота |
ϕ пропор- |
ционален пути луча l в кристалле |
|
ϕ = α l. |
(5.3.3) |