Добавил:
Вуз:
Предмет:
Файл:
ТВиМС Экзамен Подготовка + Досрочный Тест (экзамен) Литвинова.pdf
X
- •Содержание
- •Теория (лекции)
- •Алгебра событий
- •Определение (случайное событие)
- •Обозначения
- •Определение (достоверные, недостоверные)
- •Определение (обратное событие)
- •Определение (несовместное)
- •Свойства операций над событиями:
- •Определение (алгебра событий)
- •Определение (сигма алгебра событий)
- •Утверждение
- •Пример
- •Формулы для решения примитивных задач
- •Теоремы сложения умножения событий
- •Сложение
- •Умножение
- •Формула количества перестановок
- •Формула количества сочетаний
- •Формула количества размещений
- •Формула количества перестановок с повторениями
- •Формула количества сочетаний с повторениями
- •Формула количества размещений с повторениями
- •Вероятностный подход к решению задач
- •1. Классическая вероятность
- •Определение
- •Свойства
- •2. Геометрическая вероятность
- •Определение
- •3. Статистическая вероятность
- •Определение
- •Определение (мера события)
- •Утверждение
- •Условная вероятность
- •Определение
- •Утверждения
- •Определение (независимые в совокупности)
- •Утверждение
- •Формула полной вероятности. Формула Байеса
- •Теорема (формула полной вероятности)
- •Следствие (формула Байеса)
- •Пример (ФНП)
- •Пример (формула Байеса)
- •Испытание Бернулли
- •Определение
- •Теорема (формула Бернулли)
- •Пример
- •Теорема (Локальная теорема Муавра-Лапласа)
- •Свойства (функция Гаусса)
- •Пример
- •Теорема (Интегральная Муавра-Лапласа)
- •Случайные величины
- •Определение
- •Определение
- •Свойства функции распределения
- •Определение случайных величин
- •Дискретные случайные величины
- •Определение
- •Дисперсия
- •Определение
- •Свойства
- •Среднее квадратическое отклонение
- •Определение
- •Свойства
- •Начальные и центральные моменты
- •Определение (начальный момент)
- •Определение (центральный момент)
- •Формула порядка от центральных и начальных моментов
- •Определение (коэф асимметрии)
- •Определение (коэф эксцесса)
- •Определение (медиана)
- •Определение (мода)
- •Функция случайной величины
- •Определение
- •Пример
- •Теорема 1
- •Теорема 2
- •Теорема 3
- •Пример
- •Случайный вектор
- •Определение
- •Определение
- •Свойства (функции распределения)
- •Определение
- •Определение
- •Дискретный случайный вектор
- •Определение
- •Пример
- •Непрерывный случайный вектор
- •Определение
- •Свойства
- •Ковариация и коэффициенты корреляции
- •Определение
- •Свойства ковариации
- •Определение (Корреляция)
- •СВОйства
- •Пример (фото от 12:35)
- •Условные распределения для НСВ
- •Формулы
- •1. Дискретное распределение
- •Определение
- •Мат ожидание и дисперсия
- •Определение
- •Мат ожидание и дисперсия
- •Определение
- •Мат ожидание и дисперсия
- •Определение (распределение Пуассона)
- •Мат ожидание и дисперсия
- •Предельные теоремы
- •Теорема (неравенство Маркова)
- •Пример
- •Теорема (неравенство Чебышева)
- •Теорема (ЗБЧ)
- •Точечные оценки и их свойства
- •Свойства оценки
- •Определение
- •Определение
- •Определение
- •Определение
- •Теорема
- •Определение
- •Замечание
- •Нахождение точечных оценок
- •Метод моментов
- •Теорема
- •Метод максимального правдоподобия
- •Выборка из дискретного закона распределения
- •Выборка из непрерывного закона распределения
- •Пример (фото от 06.05.2024)
- •Статистическая гипотеза
- •Определение
- •Определение (простая)
- •Определение (сложная)
- •Определение (статистический критерий)
- •Критерий χ2 как критерий согласия
- •Теория (mathprofi)
- •События. Виды событий. (http://mathprofi.ru/teorija_verojatnostei.html)
- •Определение (достоверное событие)
- •Определение (невозможное событие)
- •Определение (случайное событие)
- •Определение (несовместное событие)
- •Определение (полная группа)
- •Определение (элементарность)
- •Определение (совместные события)
- •Алгебра событий
- •Обозначения
- •Определение (алгебра событий)
- •Определение (сигма алгебра событий)
- •Утверждение
- •Пример
- •Вероятность события
- •1. Классическая вероятность
- •Определение
- •Свойства
- •2. Геометрическая вероятность
- •Определение
- •3. Статистическая вероятность
- •Определение
- •Определение (мера события)
- •Утверждение
- •Формулы для решения примитивных задач
- •Теоремы сложения умножения событий
- •Сложение
- •Умножение
- •Формула количества перестановок
- •Формула количества сочетаний
- •Формула количества размещений
- •Формула количества перестановок с повторениями
- •Формула количества сочетаний с повторениями
- •Формула количества размещений с повторениями
- •Пример
- •Зависимые события и условная вероятность
- •Определение (независимое событие)
- •Определение (зависимое событие)
- •Пример
- •Теорема (умножение вероятностей зависимых событий)
- •Формула полной вероятности и формулы Байеса
- •Определение (формула полной вероятности)
- •Пример
- •Определение (Формула Байеса)
- •Пример
- •Испытание Бернулли
- •Определение
- •Теорема (формула Бернулли)
- •Пример
- •Теорема (Локальная теорема Муавра-Лапласа)
- •Теорема (Интегральная Муавра-Лапласа)
- •Теорема (Пуассона)
- •Случайные величины. Математическое ожидание
- •Определение (Случайная величина)
- •Виды случайных величин
- •Определение (Закон распределения)
- •Пример
- •Математическое ожидание дискретной случайной величины
- •Определение (мат. ожидание)
- •Свойства:
- •Дисперсия дискретной случайной величины
- •Определение (дисперсия)
- •Функция распределения дискретной случайной величины
- •Определение (функция распределения)
- •Пример
- •Непрерывная случайная величина и ее функция распределения. Функция плотности распределения
- •Определение (функция распределения НСВ)
- •Функция плотности распределения
- •Определение (плотность распределения)
- •Пример
- •Математическое ожидание и дисперсия НСВ
- •Математическое ожидание
- •Дисперсия
- •Тест (03.06)
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 7
- •Задание 8
- •Задание 9
- •Задание 10
- •Задание 11
- •Задание 12
- •Задание 13
- •Задание 14
- •Задание 15
- •Задание 16
- •Задание 17
- •Задание 18
- •Задание 19
- •Задание 22
- •Программа ТВ Литвинова
- •1.Случайные события. Основные определения и операции над ними.
- •Определение (случайное событие)
- •Обозначения
- •Определение (достоверные, недостоверные)
- •Определение (обратное событие)
- •Определение (несовместное)
- •Свойства операций над событиями:
- •2. Алгебра случайных событий
- •Определение (алгебра событий)
- •Определение (сигма алгебра событий)
- •Утверждение
- •Пример
- •3. Статистическая вероятность
- •Определение
- •Определение (мера события)
- •Утверждение
- •4.Аксиоматическая вероятность. Свойства вероятности
- •Аксиома неотрицательности
- •Аксиома нормированности
- •Аксиома аддитивности
- •Аксиома однозначности
- •СВОйства вероятности
- •5.Вероятностное пространство
- •Определение (Вероятностное пространство)
- •6.Классическая вероятность и геометрическая вероятность
- •Определение классической вероятности
- •Определение геометрической вероятности
- •7.Условная вероятность. Свойства условной вероятности.
- •Определение
- •Утверждения
- •8.Независимость событий. Независимость событий в совокупности
- •Определение (независимое событие)
- •Определение (Попарно независимы)
- •Определение (Независимы в совокупности)
- •Пример (3 монеты)
- •9.Формула полной вероятности
- •Теорема (формула полной вероятности)
- •10.Формула Байеса
- •Пример
- •11.Последовательность Бернулли
- •Определение
- •12.Наивероятнейшее число появлений события А в серии из n испытаний Бернулли
- •Теорема (формула Бернулли)
- •13. Формула Пуассона
- •14. Локальная и интегральная теоремы Муавра-Лапласа
- •Теорема (Локальная теорема Муавра-Лапласа)
- •Свойства (функция Гаусса)
- •Теорема (Интегральная Муавра-Лапласа)
- •15. Дискретная одномерная случайная величина. Ряд распределения
- •Определение (Дискретная величина)
- •Определение (Ряд распределения)
- •16. Функция распределения дискретной случайной величины
- •Свойства
- •17. Числовые характеристики дискретной случайной величины, формулы для вычисления, основные свойства
- •Определение (Математическое ожидание)
- •Свойства мат ожидания:
- •Определение (Дисперсия)
- •Свойства дисперсии
- •Определение (Среднеквадратичное отклонение)
- •Свойства среднеквадратичного отклонения
- •Определение (начальный момент)
- •Определение (центральный момент)
- •Формула порядка от центральных и начальных моментов
- •Определение (коэф асимметрии)
- •Определение (коэф эксцесса)
- •18. Непрерывная случайная величина. Функция плотности и ее свойства.
- •Определение (плотность распределения)
- •Свойства
- •19. Функция распределения АНСВ
- •Определение (Функция распределения АНСВ)
- •Формула
- •20. Числовые характеристики АНСВ, формулы для вычисления, основные свойства
- •Определение (Математическое ожидание)
- •Свойства мат ожидания:
- •Определение (Дисперсия)
- •Свойства дисперсии
- •21. Равномерное распределение и его свойства. Вычисление основных характеристик.
- •Определение (Равномерное распределение)
- •Свойства
- •22. Биномиальное распределение и его свойства. Вычисление основных характеристик
- •Определение (Биномиальное распределение)
- •Свойства
- •Пример
- •23. Распределение Пуассона и его свойства. Вычисление основных характеристик
- •Определение (Распределение Пуассона)
- •Свойства
- •24. Показательное распределение и его свойства. Вычисление основных характеристик
- •Определение (Показательное распределение)
- •Свойства
- •26. Распределение Лапласа и его свойства. Вычисление основных характеристик.
- •27. Двойное экспоненциальное распределение и его свойства. Вычисление основных характеристик.
- •28. Нормальное распределение и его свойства. Вычисление основных характеристик.
- •Определение
- •Свойства
- •Функция плотности:
- •29. Распределения, связанные с нормальным законом и их свойства.
- •Определение (Гамма-распределение)
- •Свойства
- •Определение (хи-квадрат)
- •Свойства:
- •30. Двумерный дискретный случайный вектор и его характеристики
- •Определение (дискретный случайный вектор)
- •Характеристики:
- •Пример
- •31. Двумерный непрерывный случайный вектор и его характеристики
- •Определение (НСВ)
- •Свойства
- •32. Функция случайной величины в дискретном и непрерывном случаях
- •33. Функция случайного вектора в дискретном и непрерывном случаях
- •34. Независимые случайные величины. Ковариация и коэффициент корреляции случайных величин
- •Определение (Независимые случайные величины)
- •Ковариация и коэффициент корреляции
- •Свойства ковариации
- •Определение (Корреляция)
- •СВОйства
- •35. Условное математическое ожидание и его свойства
- •Условное мат. ожидание
- •Свойства
- •36. Неравенства Чебышева и Маркова
- •Теорема (неравенство Маркова)
- •Теорема (неравенство Чебышева)
- •Пример
- •37. Закон больших ч(ленов)исел
- •Теорема (Закон Больших Чисел)
- •38. Центральная предельная теорема Ляпунова
- •Теорема (ЦПТ Ляпунова)
- •Программа математической статистики
- •1. Выборочный метод. Основные понятия
- •Определение (выборка)
- •Определение (вариационный ряд)
- •2. Выборочные характеристики. (выборочное среднее, выборочная дисперсия, выборочные моменты, выборочная мода, выборочная медиана, эмпирическая функция распределения, выборочная асимметрия, выборочный эксцесс).
- •Выборочное среднее
- •Выборочная дисперсия
- •Выборочные моменты
- •Выборочная мода
- •Выборочная медиана
- •Эмпирическая функция распределения
- •Выборочная асимметрия
- •Выборочный эксцесс
- •3. Свойства выборочного среднего
- •Свойства
- •4. Свойства выборочной дисперсии
- •Свойства
- •5. Свойства эмпирической функции распределения
- •Свойства
- •6. Состоятельность, несмещенность, эффективность оценок в смысле среднеквадратичного подхода
- •Определение (состоятельность)
- •Определение (несмещенность)
- •Определение (эффективность оценки)
- •7. Метод моментов Пирсона (из рдр2 повар)
- •Теорема (метод маметов Пирсона)
- •8. Свойства оценок метода моментов
- •9. Метод максимального правдоподобия
- •10. Сравнение оценок в смысле среднеквадратичного подхода
- •11. Асимптотически нормальные оценки и их свойства
- •Пример (?)
- •12. Сравнение оценок в смысле асимптотического подхода
- •Определение (сравнение АНО)
- •13. Неравенство Рао-Крамера
- •14. Интервальные оценки
- •Определение (интервальные оценки)
- •15. Лемма Фишера и следствия из нее. Построение доверительных интервалов для выборки из нормального закона
- •Лемма (Фишера)
- •Следствия (лемма Фишера)
- •17. Статистические критерии
5. Сумма большого числа независимых случайных величин, каждая из которых имеет одно и то же распределение, будет приближаться к нормальному распределению.
Функция плотности:
( −µ)2
( ) = |
σ· 2π |
· |
|
; µ |
|
|
1 |
− |
2σ2 |
|
– мат ожидание |
29. Распределения, связанные с нормальным законом и их свойства.
Это гамма-распределение, распределение хи-квадрат, стьюдента(?) и фишера(?)
Определение (Гамма-распределение)
Это непрерывное распределение, ограниченное снизу. Пусть распределение случайной величины 
задается плотностью вероятности, имеющей вид:
|
, где |
– гамма функция |
|
Тогда говорят, |
что случайная величина |
имеет гамма-распределение с положительными |
|
параметрами и |
|
|
|
Свойства |
|
|
|
1) Пусть |
независимы, и имеет гамма распределение |
. Тогда: |
|
имеет распределение 
че за хуетень
2) Если 
имеет стандартное нормальное распределение, то 
имеет Гамма-распределение
Определение (хи-квадрат)
Распределение суммы 
квадратов независимых стандартных нормальных случайных величин называют распределением хи-квадрат с 
степенями свободы
Свойства:
1) Если 
независимы и имеют стандартное нормальное распределение, то случайная
величина 
имеет гамма-распределение 
2) Если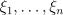 
независимы и имеют нормальное распределение 
, то
имеет 
-распределение с 
степенями свободы
Соседние файлы в предмете Теория вероятностей и математическая статистика