
2024 ТВИМС ИДЗ 2
.pdf
Студент:
Группа:
Вариант:
Дата:
Теория вероятностей и математическая статистика Индивидуальное домашнее задание №2
Задание 1. Дана функция распределения случайной величины ξ: |
|
|
|
|
|||||||||||||||||||
x |
(−∞, − 3] (−3, − 2] (−2, − 1] (−1,1] (1, − ∞) |
||||||||||||||||||||||
Fξ(x) |
0 |
|
|
|
1/7 |
3/7 |
|
6/7 |
|
1 |
|
|
|||||||||||
Вычислить Eξ, Dξ, Hξ (в натах). Вычислить распределение η |
= ξ3. Построить графики функций |
||||||||||||||||||||||
распределений Fξ(x) и Fη(y). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pi |
−3 |
|
|
−2 |
|
−1 |
|
1 |
P |
|
|
|
|
||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1/7 |
2/7 |
|
3/7 |
|
|
1/7 |
1 |
|
|
|
|
|
|
|
|||||
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i:Xpi |
|
|
1 |
2 |
|
|
3 |
1 |
9 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= −3 · 7 + (−2) · 7 + (−1) |
· 7 + 1 · 7 = −7 |
||||||||||||||||||||||
Eξ = |
ai · pi |
||||||||||||||||||||||
|
>0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2)
Dξ = Eξ2 − (Eξ)2
Eξ2 = X a2i · pi = 9 · 17 + 4 · 27 + 1 · 37 + 1 · 17 = 3
i:pi>0
Dξ = 3 − 8149 = 6649
3)
|
|
|
|
Hξ = − |
pXi |
|
· ln (pi) |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
>0 |
pi |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Hξ = −( |
1 |
|
1 |
|
2 |
|
2 |
3 |
|
3 |
|
|
1 |
|
1 |
|||||||||
|
· ln |
|
+ |
|
|
|
· ln |
|
|
+ |
|
|
· ln |
|
+ |
|
|
· ln |
|
|
) ≈ 1.277 |
|||
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
|||||||||||||||||
|
|
|
|
|
|
|
|
η = ξ3; |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
ξ |
|
|
|
−3 |
|
|
−2 |
|
−1 |
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
ξ |
|
|
|
−27 |
−8 |
|
−1 |
|
|
|
|
|
|
|
||||||
P(η = −27) = P(ξ = −3) = 1/7
P(η = −8) = P(ξ = −2) = 2/7
P(η = −1) = P(ξ = −1) = 3/7
P(η = 1) = P(ξ = 1) = 1/7
1

Рис. 1 — График Fξ(x)
Рис. 2 — График Fη(y)
Задание 2. Дана плотность распределения абсолютно непрерывной случайно величины ξ:
pξ(x) = C exp(−|x + 3|), x R
Вычислить C, Eξ, Dξ, Hξ (в натах). Вычислить распределение η = ξ3. Построить графики функций распределений Fξ(x) и Fη(y).
2

Решение.
Z ∞
C exp(−|x + 3|) = 1
−∞
Z ∞
Cexp(−|x + 3|) = 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z−∞ exp(−|x + 3|) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Z−3 |
exp(−x − 3) = −e−x−3 |
∞ |
= 0 − (−1) = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
= 1 − 0 = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z−∞ exp(x + 3) = ex+3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
= 1 + 1 C = |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
∞ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−3 |
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||
Eξ = Z−∞ x·pξ(x)dx = Z−∞ x· |
|
|
·exp(−|x+3|)dx = |
|
|
|
(Z−3 |
x·exp(−x−3)dx+Z−∞ x·exp(x+3)dx) = |
|
|
·(−2+(−4)) = −3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dξ = Eξ2 − (Eξ)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
E(ξ2) = |
|
|
|
·Z−∞ x2 |
·exp(−|x+ 3|) = |
|
|
(Z−3 |
x2 ·exp(−x−3)dx+ Z−∞ x2 |
·exp(x+ 3)dx) = |
|
·(5 + 17) = 11 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
2 |
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dξ = 11 − 9 = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
Hξ = − Z−∞ |
|
exp(−|x + 3|) · ln ( |
|
exp(−|x + 3|))dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
∞ |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−3 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
= − |
|
(Z−3 |
exp(−x − 3) ln ( |
|
|
exp(−x − 3))dx + Z−∞ exp(x + 3) ln ( |
|
exp(x + 3))dx) = |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
|
· (− ln(2) − 1 + (− ln(2) − 1)) = −(− ln(2) − 1) ≈ 1.693 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
Распределение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fξ(x) [0; 1] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
x (−∞; −3) Fξ(x) = Z−∞ |
2 exp(x + 3)dx = |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
exp(x + 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
−3 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
exp( |
x |
|
3) |
|
||||||||||||||||
x (−3; ∞) Fξ(x) = Z−∞ |
|
exp(x+3)dx+Z−3 |
|
|
|
exp (−x − 3)dx = |
|
|
·(1+1−exp(−x−3)) = |
|
|
+ |
|
|
− |
|
− |
− |
|
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
2 |
2 |
2 |
2 |
|
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1 |
− |
exp(−x − 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 |
|
|
|
|
|
|
|
|
2 |
|
x ( 3; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ |
|
|
|
|
|
exp(−x−3) |
, |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
exp(x+3) |
|
|
|
|
, x (−∞; −3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (x) = |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
− |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3
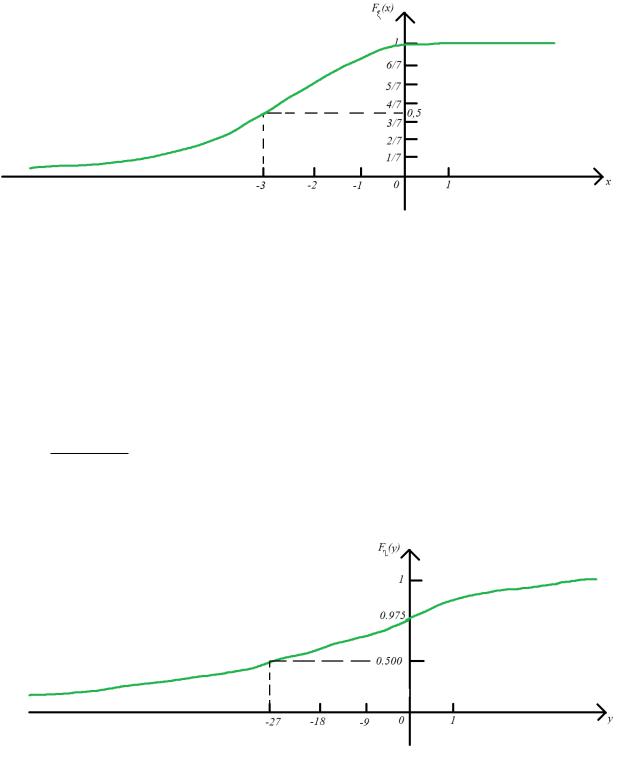
Рис. 3 — График Fξ(x)
Рассчитаем для η = ξ3
supp ξ = (−∞; +∞); supp η = (−∞; +∞) = (−∞; −27] [27; +∞)
|
|
|
|
|
|
|
|
|
Fη(y) = P(η < y) = P(ξ3 < y) = P(ξ < √3 |
|
) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
y |
||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
pη(y) = |(g−1(y))′| · pξ(g−1(y)) |
|
|
|
||||||||||||
y (−∞; −27) pη(y) = |
|
|
· exp(y + 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
6 |
3 |
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
y |
( 27; + ) |
|
p (y) = |
|
p |
|
exp( y 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
− ∞ η |
|
|
1 |
|
· − − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
6 |
3 |
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
p |
(y) = |
exp(−|y + 3|) |
, y |
|
( p |
; + |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
η |
6 3 |
y2 |
|
|
−∞ |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, y |
(−∞; −27] |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
F |
(y) = |
|
|
2 |
|
|
3 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
exp(− |
|
|
|
, y |
|||||||||||||||
|
|
|
|
|
|
|
|
η |
|
(1 |
|
√y−3) |
[ 27; |
) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
exp( √y+3) |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
− |
∞ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||
Рис. 4 — График Fη(y)
4
