Добавил:

triple666mafia north memphis Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Теория вероятностей и математическая статистика

Файл:

2024 ТВИМС ИДЗ 4

.pdf

Скачиваний:

Добавлен:

13.06.2024

Размер:

260.46 Кб

Скачать

☆

Студент:

Группа:

Вариант:

Дата:

Теория вероятностей и математическая статистика Индивидуальное домашнее задание №4

α = 0.1; c = −9; d = 5; h = 4; a0 = 1; σ0 = 10; a1 = −32; σ1 = 10
Таблица 1.	− 16.39 − 8.84 5.84	8.88 0.56 11.10 − 14.77 − 1.36	− 1.25		−
−5.81 3.01 − 5.79 13.32				15.95
3.72 7.87 3.38 5.13 29.68 5.64 − 1.41 10.18 6.97		− 4.02 5.41 − 3.72 9.09 − 8.79 − 4.72 − 5.10			−
2.43 9.56 − 17.61 − 12.03	− 9.62 − 12.50 6.16 13.40 − 7.67 2.88 0.06 − 0.76 11.88		− 5.36	− 0.75	−
14.77 3.72 4.25 24.77 − 0.24

Задание 1. Построить вариационный ряд, эмпирическую функцию распределения, гистограмму и полигон частот с шагом h.

Решение. Вариационный ряд:

-17,61 -16,39 -14,77 -14,77 -12,50 -12,03 -9,62 -8,84 -8,79 -7,67 -5,81 -5,79 -5,36 -5,10 -4,72 -4,02 -3,72 -3,72 -2,43 -1,41 -1,36 -1,25 -0,76 -0,75 -0,24 0,06 0,56 2,88 3,01 3,38 3,72 4,25 5,13 5,41 5,64 5,84 6,16 6,97 7,87 8,88 9,09 9,56 10,18 11,10 11,88 13,32 13,40 15,95 24,77 29,68

(xi; xi+1]	ni	ni	ni	F
(xi; xi+1]	ni	n	h	F
[−17,61; −13,61]	4	0,08	1	0,08
(−13,61; −9,610]	3	0,06	0,75	0,14
(−9,610; −5,610]	5	0,10	1,25	0,24
(−5,610; −1,610]	7	0,14	1,75	0,38
(−1,610; 2,390]	8	0,16	2	0,54
(2,390; 6,390]	10	0,20	2,5	0,74
(6,390; 10,39]	6	0,12	1,5	0,86

(10,39; 14,39]	4	0,08	1	0,94
(14,39; 18,39]	1	0,02	0,25	0,96

(18,39; 22,39]	0	0	0	0,96

(22,39; 26,39]	1	0,02	0,25	0,98

(26,39; +∞]	1	0,02	0,25	1
	50	1

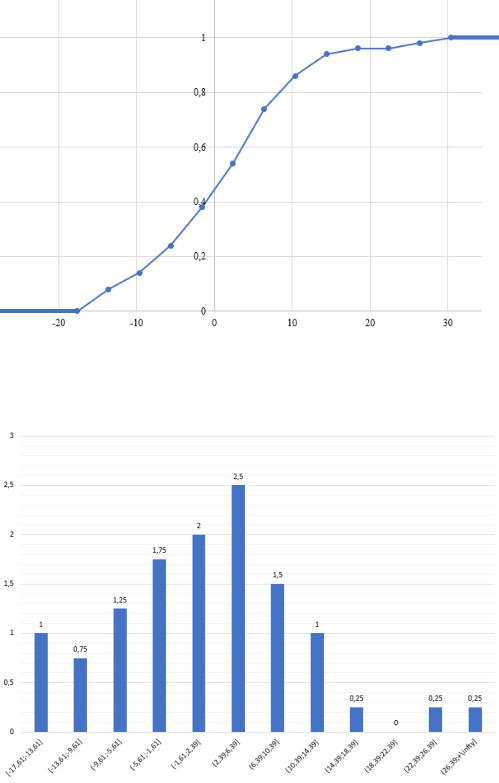
Функция распределения:

Рис. 1 — Функция распределения

Гистограмма:

Рис. 2 — Гистограмма

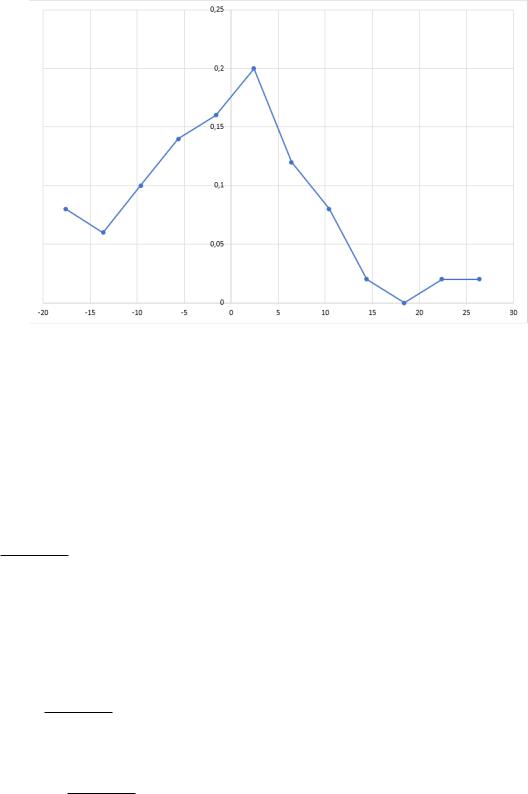
Полигон частот:

Рис. 3 — Полигон частот

Задание 2. Вычислить выборочные аналоги следующих числовых характеристик: 1) математического ожидания, 2)дисперсии, 3)СКО, 4)медианы, 5)асимметрии, 6)эксцесса, 7)вероятности P(X

[c; d]).

Решение.

Аналог мат. ожидания

x1 + x2 + . . . + xn

49,26

= 0,9852

Аналог дисперсии

σ2

P(n i −1

= 98,6238

−

Аналог СКО

σ = √

= 9,931

σ2

4)Медиана

Me = −0,09

5)Ассиметрия

µ3

(n i −1

418,92

A =

−

= 0,4277

σ3

9,9313

6) Эксцесс

(n i −1

µ4

E =

− 3 =

−

− 3 = 3,33 − 3 = 0,33

σ4

7) вероятность P(X [c; d])

X [−9; 5]; X N(0,9852; 98,6238)

5 − 0,9852

P(X [−9; 5]) = F ( 9,931 ) − F (

− 9 − 0,9852

) = F (0,4043) − F (| − 1,005|) = 0,1554 + 0,3438 = 0,4992

9,931

Задание 3. В предположении, что исходные наблюдения являются выборкой из нормального распределения, построить оценку максимального правдоподобия параметров (a,σ2) и соответствующие оценки по методу моментов.

ˆ2

)

Решение. ОМП (ˆa,σ

) параметра (a,σ

σ2

= 0

− n · aˆ

aˆ =

(xi aˆ)

ˆ2

−

= σ

= 0

2σ2

P2(σ2)2

· P

−

по методу моментов:

Оценки

	(σˆ2 = 98,6238
	aˆ = 0,9852

aˆ = n ·						xi = x = 0,9852
			1
		2		1 P				2	2
	ˆ
σ			=	n		(xi	−	aˆ) = σ	= 98,6238
				n	· P		−

Задание 4. Построить доверительные интервалы уровня доверия 1 − α для параметров (a,σ2).

Решение.

√x − a

−xα ≤ n − 1 ·

≤ xα

"X − √n

· 1; X + √n

xα

−

Iα = [x1α; x2α]

x1α : Kn−1(x1α) = 2

x2α : Kn−1(x2α) = 1 − 2

xα = 2,0096 [−1,866; 3,8362] a

σ2

n · s2

;

n · s2

χα

1−

= 67,5048;

= 33,9303 σ

[73,0495; 145,3329]

χ1− 2

Задание 5. Используя гистограмму частот, построить критерий значимости χ2 проверки просто гипотезы согласия с нормальным распределением с параметрами (ai,σi2), i = 0; 1. Проверить гипотезу на уровне значимости α.

Решение.

Таблица 1 с параметрами (a0 = 1, σ0 = 10)

														2			(vj − n · pˆj)2
		(xi; xi+1]						vj			pˆj	n · pˆj	(vj − n · pˆj)				n · pˆj
		[−∞; −13,61]						4			0,0720	3,6004	0,1597				0,0444
		(−13,61; −9,610]						3			0,0723	3,6169	0,3805				0,1052
		(−9,610; −5,610]						5			0,1100	5,4981	0,2481				0,0451
		(−5,610; −1,610]						7			0,1427	7,1370	0,0188				0,0026
		(−1,610; 2,390]						8			0,1582	7,9114	0,0078				0,0010
		(2,390; 6,390]						10			0,1498	7,4891	6,3047				0,8419

		(6,390; 10,39]						6			0,1211	6,0539	0,0029				0,0005
		(10,39; 14,39]						4			0,0836	4,1790	0,0320				0,0077

		(14,39; 18,39]						1			0,0493	2,4634	2,1415				0,8693
		(18,39; 22,39]						0			0,0248	1,2400	1,5375				1,2400

		(22,39; 26,39]						1			0,0107	0,5330	0,2181				0,4093
		(26,39; +∞]						1			0,0056	0,2779	0,5214				1,8760
xα : Kr d 1(xα) = 1P α K							10	(xα) =			0,95				P		ˆ2
xα : Kr d 1(xα) = 1P α K							10	(xα) =			0,95	n = 50			P		= X	= 5,4429
							n = 50				1	n = 50					= X	= 5,4429
	− −		−
								ˆ	2	< xα φ(x) = 0
K10(xα) = 0,95 xα = 18,3070 X										< xα φ(x) = 0
Таблица 2 с параметрами (a1 = −32, σ1 = 10)
		(xi; xi+1]						vj			pˆj	n · pˆj	(vj − n · pˆj)	2			(vj − n · pˆj)2
														2			(vj − n · pˆj)2
																	n · pˆj
		[−∞; −13,61]						4			0,9670	48,352	1967,1				40,683
		(−13,61; −9,610]						3			0,0204	1,0190	3,9244				3,8513
		(−9,610; −5,610]						5			0,0084	0,4210	20,967				49,800
		(−5,610; −1,610]						7			0,0030	0,1485	46,943				316,03
		(−1,610; 2,390]						8			0,0009	0,0447	63,286				1414,4
		(2,390; 6,390]						10			0,0002	0,0115	99,770				8669,4

		(6,390; 10,39]						6			0,0001	0,0025	35,970				14233

		(10,39; 14,39]						4			0,0000	0,0005	15,996				33763

		(14,39; 18,39]						1			0,0000	0,0001	0,9998				13186

		(18,39; 22,39]						0			0,0000	0,0000	0,0000				0,0000
		(22,39; 26,39]						1			0,0000	0,0000	1,0000				827659

		(26,39; +∞]						1			0,0000	0,0000	1,0000				7616859
	α : Kr d 1(xα) =P					10 α									P		ˆ2
	α : Kr d 1(xα) =P					10 α					1	n = 50			P	= X		= 8516196
							n = 50				1	n = 50				= X		= 8516196
x	− −	1	−	α	K (x ) = 0,95
x		1		α	K (x ) = 0,95
								ˆ	2	> xα φ(x) = 1
K10(xα) = 0,95 xα = 18,3070 X										> xα φ(x) = 1

Задание 6. Построить критерий проверки значимости χ2 сложной гипотезы согласия с нормальным распределением. Проверить гипотезу на уровне значимости α.

Решение. Таблица с параметрами (a = 0,9852, σ = 9,931)

													2		(vj − n · pˆj)2
						(xi; xi+1]		vj			pˆj	n · pˆj	(vj − n · pˆj)		n · pˆj
						[−∞; −13,61]		4			0,0708	3,5413	0,2104		0,0594
						(−13,61; −9,610]		3			0,0722	3,6093	0,3712		0,1029
						(−9,610; −5,610]		5			0,1103	5,5150	0,2652		0,0481
						(−5,610; −1,610]		7			0,1436	7,1805	0,0326		0,0045
						(−1,610; 2,390]		8			0,1593	7,9662	0,0011		0,0001
						(2,390; 6,390]		10			0,1506	7,5308	6,0972		0,8096
						(6,390; 10,39]		6			0,1213	6,0662	0,0044		0,0007

						(10,39; 14,39]		4			0,0833	4,1637	0,0268		0,0064
						(14,39; 18,39]		1			0,0487	2,4352	2,0597		0,8458

						(18,39; 22,39]		0			0,0243	1,2135	1,4726		1,2135

						(22,39; 26,39]		1			0,0103	0,5153	0,2350		0,4560

						(26,39; +∞]		1			0,0053	0,2631	0,5430		2,0641
						(xα) = 1P α		n = 50			1	n = 50		P	ˆ2 = 5,6112
xα	: Kr														= X
xα	: Kr	−	d	−	1		K10(xα) = 0,95
		−		−		−
								ˆ	2	< xα φ(x) = 0
K10(xα) = 0,95 xα = 18,3070 X										< xα φ(x) = 0

Соседние файлы в предмете Теория вероятностей и математическая статистика

#
13.06.2024221.3 Кб12024 ТВИМС ИДЗ 1.pdf
#
13.06.2024224.64 Кб12024 ТВИМС ИДЗ 2.pdf
#
13.06.2024367.78 Кб42024 ТВИМС ИДЗ 3.pdf
#
13.06.2024260.46 Кб12024 ТВИМС ИДЗ 4.pdf