Добавил:

triple666mafia north memphis Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Теория вероятностей и математическая статистика

Файл:

2024 ТВИМС ИДЗ 3

.pdf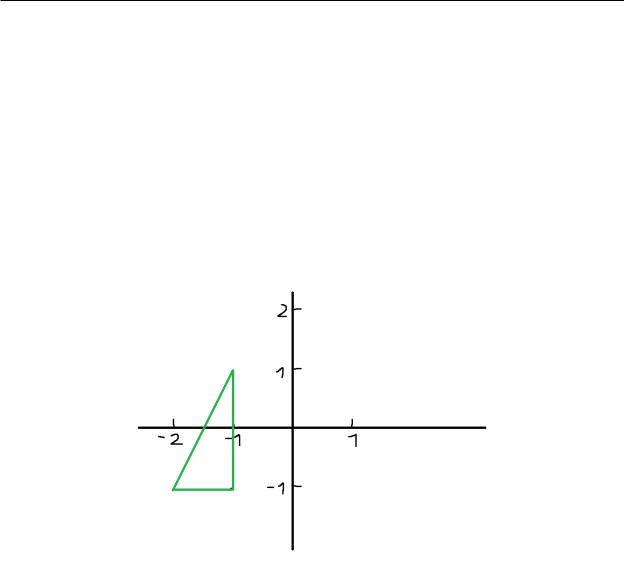

Скачиваний:

Добавлен:

13.06.2024

Размер:

367.78 Кб

Скачать

☆

Студент:

Группа:

Вариант:

Дата:

Теория вероятностей и математическая статистика Индивидуальное домашнее задание №3

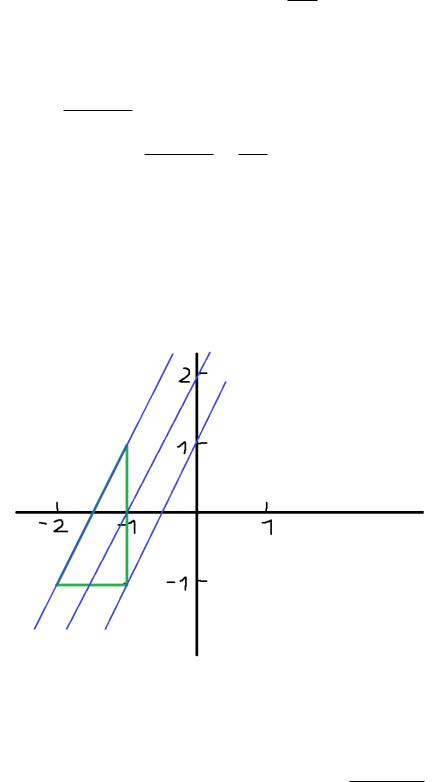
Случайный вектор (ξ,η) имеет равномерное распределение в области D:

D =	2x − y ≥ −3
	x ≤ −1, y ≥ −1

ζ = 1ξ4 − 3, ν = [5η], µ = −4ξ + 2η

Задание 1. Найти pξ,η(x,y), функции и плотности распределения компонент. Построить графики функций распределений Fξ(x) и Fη(y). Будут ли компоненнты независимыми?

Решение.

x ≤ −1, y ≥ −1 x ≤ −1, y ≥ −1
D = 2x − y ≥ −3	= y ≤ 2x + 3

Рис. 1 — Область пересечения графиков

C, (x,y) D pξ,η(x,y) = 0,else

R RD pξ,η(x,y)dxdy = 1 · 2 · 12 = 1

−1	2x+3	−1		C = 1
R−2	dx R−1	Cdy = C · R−2	(2x + 4)dx = 1	C = 1

Получаем, что
	pξ,η(x,y) =	1, (x,y) D
		0,else
fξ(x):
2x+3	1 · dy = 2x + 4
fξ(x) = RR pξ,η(x,y) = R−1	1 · dy = 2x + 4

fξ(x) =

2x + 4, x [−2, − 1]

fη(y):

0, x / [−2, − 1]

(y) =

−1

1 dx =

−

−2

fη

(y) =

, y [−1,1]

0, y / [−1,1]

Плотность распределения

Fξ(x), x (−∞; −2] =

x∞ 0 · dx = 0

Fξ(x), x [ 2; 1] =

R−−2 0 dx +

x2 2x + 4dx = x2 + 4x + 4

Fξ(x), x [ 1; + ) =R

−2

0 dx +R

−21

2x + 4dx + x1 0 dx = 0 + 1 + 0 = 1

−

−∞

−

R− ·

− ∞

R−∞ ·

R−

[

Fξ(x) =

+ 4x + 4 , x

1])

, x

(−∞; −2]

, x

−

)

[

1; +

−

∞

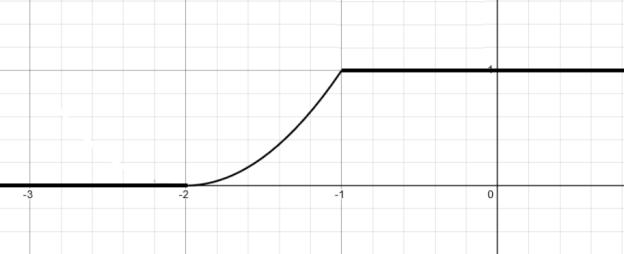
Рис. 2 — График распределения Fξ(x)

Fη(y), y (−∞; −1] =

−y∞ 0 · dy = 0

−2

dy =

−4

−

Fη(y), y [ 1; 1] =

0 dy +

−1

Fη(y), y [1; +∞) =RR−−∞1

0 · dy +RR−11

1−2 y dy + R1y

0 · dy = 0 + 1 + 0 = 1

−

−∞

−

Fη(y) =	y			−4 −		, y		[ 1; 1])
		0	2	2y	3	, y		(−∞; −1]
	1					,	y	[1; + )
						,		∞

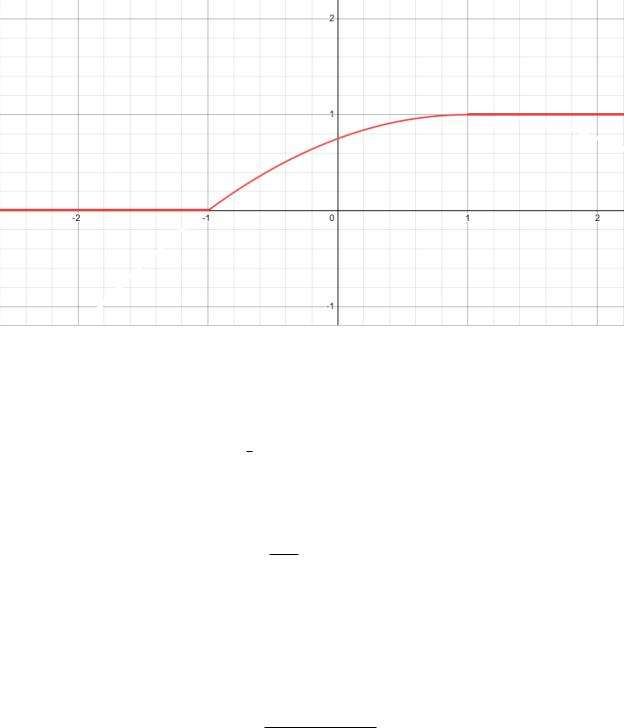
Рис. 3 — График распределения Fη(y)

Пусть (x,y) = (−1; −1), тогда pξ,η(−1, − 1) = 1

fξ(−1) = 2; fη(−1) = 2 = 1; fξ(−1) · fη(−1) = 1 ≠ pξ,η(−1, − 1)

Компоненты зависимы

Задание 2. Найти распределения случайных величин ζ и ν. Вычислить Eζ, Dζ, Eν и Dν. Построить графики функций распределений Fζ(z) и Fν(n).

Решение.	√4 z + 3)
Fζ(z) = P(ζ < z) = P(1ξ4 − 3 < z) = P(ξ <

supp ξ = [−2; −1] supp ζ[−2; 13] pζ(z) = (|g−1(y)|)′ · pξ(g−1(y))

Поскольку Функция убывает, снимаем модуль с минусом:

A = [−2; 13] (g−1(z) =

−√4

z + 3

g(x) = x4

(2 · (−√4

−

√4

z + 3) + 4)

(z) =

(

z + 3)′

(

z + 3) + 4) =

−

4 q4 (z + 3)3

√

(2 · (− 4 z + 3) + 4)

pζ(z) = 4 4 (z + 3)3

,z [−2; 13])

,z else

Поскольку функция убывает, формула распределения выглядит так:

Fζ(z) = 1 − Fξ(g−1(z))

Fζ(z) =

((

√4 z + 3))2

(

√4 z + 3)

4 , z

[ 2; 13])

, z (−∞;

−2]

−

· −

−

, z

−

)

[13; +

∞

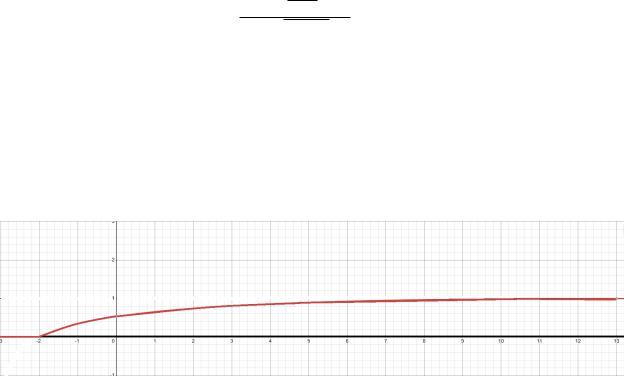
Рис. 4 — График Fζ(z)

Мат. ожидание:

√4

+ 4

z + 3

Eζ = Z−2 z ·

−

dz =

(z + 3)3

Дисперсия:

√4

E(ζ2) = R−132 z2

z + 3

+ 4

dz = 39245

· 4 (z + 3)3

392

1816

Dζ = E(ζ

) − (E(ζ))

−

225

ν = 5η supp η = [−1; 1] supp ν = [−5; 5] = {−5; −4; −3; −2; −1; 0; 1; 2; 3; 4; 5}

−1+((i+1)·

(1−(−1)

)

≤

Z−1+(i·(1−10−

pν(y)dy

P(νi) =

(

, i

1; i

supp ν

−5

−4

−3

−2

−1

Pνi

19/100

17/100

15/100

13/100

11/100

9/100

7/100

5/100

3/100

1/100

0/100

P = 1

Мат. ожидание:

Eν = P(νi) · vi = 0,19 · (−5) + . . . + 0 · 5 = −2,15

Дисперсия:

E(ν2) = PP(νi) · (vi)2 = 0,19 · (−5)2 + . . . + 0 · 52 = 10,15

Dν = E(ν2) − (Eν)2 = 10,15 − 4,6225 = 5,5275

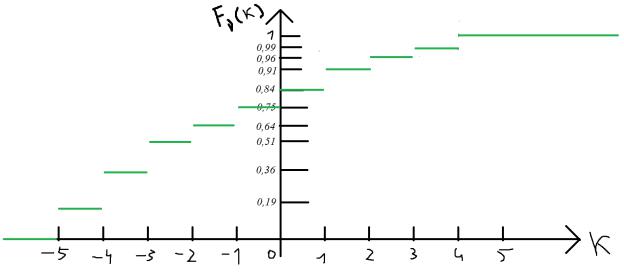
Функция распределения:

k	(−∞; −5]	(−5; −4]	(−4; −3]	(−3; −2]	(−2; −1]	(−1; 0]	(0; 1]	(1; 2]	(2; 3]	(3; 4]	(4; +∞)
Fν(k)	0	19/100	36/100	51/100	64/100	75/100	84/100	91/100	96/100	99/100	1

Рис. 5 — График распределения Fν(k)

Задание 3. Вычислить вектор математических ожиданий, построить ковариационную и корреляционную матрицы для вектора (ξ,η). Найти условное распределение ξ при условии η. Вычислить

E(ξ|η) и D(ξ|η)

Решение.

Вектор математических ожиданий

ξ= (ξ1, . . . ,ξn); Eξ = (Eξ1, . . . ,Eξn)

Eξ = −−21 x · (2x + 4)dx = −34

Eη = R

1 y

2 dy =

1−y

R−

−

(ξ,η) = (

;

−

Матрица ковариации

cov(ξ,η) = E(ξ · η) − E(ξ) · E(η)

ξ:

Dξ = Eξ2 − (Eξ)2

Eξ2 = R−−21 x2(2x + 4)dx = 116

ξ =

= 1

η:

−

Dη = Eη1 −

(Eη)

Eη2 = R−1 y2

1−2 y

dy = 31

η =

1 1

−

E(ξη) =

R R

−1

2x+3

−1

R2 x · y · pξ,η(x,y)dxdy = −2 xdx

−1

ydy =

−2 (2x

+ 6x

+ 4x)dx = 2

cov(ξ,η) =

−

X18 18

Корреляционная матрица

√

cov(ξ,η)

ρ(ξ,η) =

√

√·

R =

· D

Условное распределение ξ при условии η

(0−

, else

(0−

, else

−

ξ|η

pη(y0)

1 − y0

ξ|η=y0

η−3

pξ,η(x,y0)

, (x,yo)

, x [

;

(x) =

1 η

Мат. ожидание:

(ξ η) =

−1 x

dx =

η − 5

−

· 1

η−3

Дисперсия:

D(ξ|η) = E(ξ2|η) − (E(ξ|η))2

(ξ2

η) =

η−13

2x2

dx =

(η − 3)3 + 8

1 − η

12 η − 12

R 2

−

(ξ

η) =

(η − 3)3 + 8

−

(

η − 5

(η − 1)3

12 η

−

12η

−

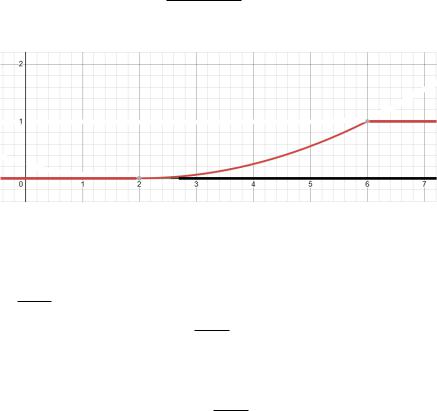
Задание 4. Найти распределение µ. Вычислить Eµ и Dµ. Построить график функции распределения

Fµ(m).

Решение. µ = −4ξ + 2η

Z Z

Fµ(m) = P(µ < m) = P(−4ξ + 2η < m) Fµ(m) = pξ,η(x; y)dxdy

−4ξ+2η<m

Поскольку ξ [−2; −1] и η [−1; 1], то supp µ = (2; 6] m (2; 6]

Рис. 6 — График

	−1		4x+m			−1		m		m2 − 4m + 4
Fµ(m) =		dx	2	Cdy =			(2 x +		+ 1)dx =
	−−4		Z−1		Z	−−4
Z							2		16
	m 2					m 2

Отсюда получаем, что:

Fµ(m) =

m2 − 4m + 4

,m (−∞; 2]

,m (2; 6]

,m (6; +∞)

Рис. 7 — График Fµ(m)

Плотность распределения:

pµ(m) = Fµ′ (m) =

m − 2

pµ(m) =

− 2

(2; 6]

, else

Мат. ожидание:

µ =

m − 2

dm =

Дисперсия:

m − 2

Dµ = E(µ2) − (E(µ))2

E(µ

) =

R2 m

dm =

196

Dµ =

−

Соседние файлы в предмете Теория вероятностей и математическая статистика

#
13.06.2024221.3 Кб12024 ТВИМС ИДЗ 1.pdf
#
13.06.2024224.64 Кб12024 ТВИМС ИДЗ 2.pdf
#
13.06.2024367.78 Кб42024 ТВИМС ИДЗ 3.pdf
#
13.06.2024260.46 Кб12024 ТВИМС ИДЗ 4.pdf