2024 ТВИМС ИДЗ 1

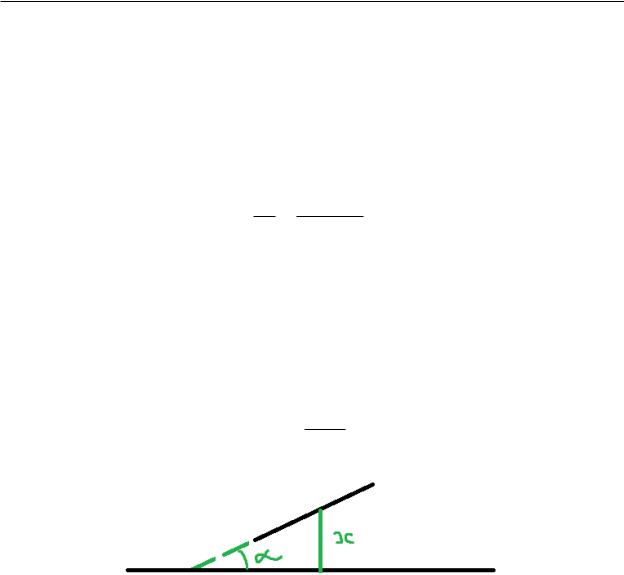
Студент:

Группа:

Вариант:

Дата:

Теория вероятностей и математическая статистика

Индивидуальное домашнее задание №1

Задание 1. Известно, что среди 70 лампочек имеется 8 перегоревших. Вычислить вероятность того, что для выявления всех перегоревших лампочек, потребуется проверить не более половины.

Решение. Количество вариантов разместить 8 перегоревших лампочек в первых 35 — 358 Количество вариантов разместить 8 перегоревших лампочек среди всех 70-ти — 708 Отсюда получаем, что:

35

P(A) = 708 = 944035092023535820 ≈ 0,0023

8

Ответ: 0,0023

Задание 2. Прямые разбивают плоскость на полосы ширины 6. Определить вероятность того, что отрезок длины 3, наугад брошенный на плоскость, не пересечет ни одной прямой.

Решение. Пусть l — длина отрезка, d — расстояние между полосами, α — угол между отрезком и прямой, а x — это расстояние от центра отрезка до ближайшей прямой.

Решение будет строится от обратного: следует найти вероятность того, что наугад брошенный отрезок пересечет прямую.

Тогда получим, что

x ≤ l · sin α 2

Рис. 1 — Схематичное изображение обозначений

Также, согласно тому, что ищется вероятность пересечения прямой, следует отметить, что 0 < x < d2 , поскольку 0 < l < d и 0 < α < π2

Множество всех возможных исходов для значений расстояния от центра упавшего отрезка до прямой ( x ) и углом между отрезком и прямой ( α ) — это прямоугольник со сторонами d2 и π2 соответственно.

Но поскольку в самом начале было обозначено неравенство, то множество всех возможных исходов для значений расстояния от центра упавшего отрезка до прямой — это уже область под графиком

l· sin α (оранжевый цвет на рис. 2).

2

1

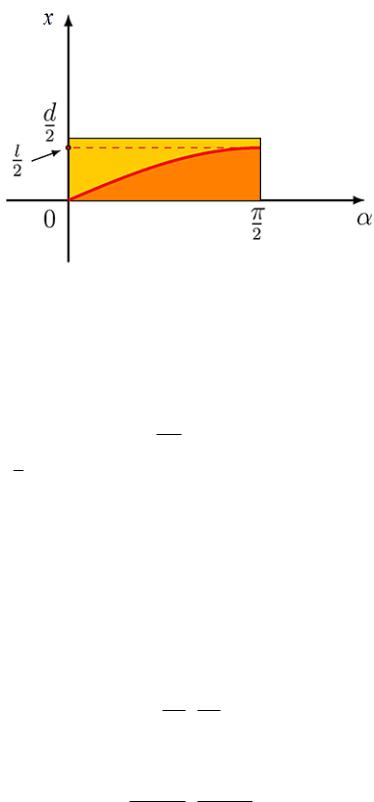
Рис. 2 — Изображение множества всех возможных исходов

Отсюда получаем, что решением является отношение двух площадей:

Поскольку полученная вероятность — это вероятноть пересечения отрезка и прямой, то искомая вероятность: P(A) = 1 − P(A) = 0,6817

Ответ: 0,6817

Задание 3. В первой урне находится 16 белых и 12 черных шаров; во второй — 10 белых и 16 черных шаровю Одновременно из первый во второй урну наугад перекладывают 3 шара; из второй урны в первую перекладывают 2 шара. Затем из второй урны достают шар. Он белый. Определить вероятность того, что в первой урне осталось столько же белых шаров, сколько было вначале.

Решение. Пусть A — событие, что в первом ящике осталось столько же белых шаров, сколько и было изначально. Это значит, что либо из первой урны взяли 3 черных и вернули 2 черных, либо взяли 1 белый 2 черных и вернули 1 белый 1 черный, либо взяли 2 белых 1 черный и вернули 2 белых.

Рассмотрим первый случай. Пусть событие B1 — событие что из первой урны взяли 3 черных и вернули 2 черных:

12 19

P(B1A) = 283 · 292 = 0,0283

32

Рассмотрим второй случай. Пусть событие B2 — событие что из первой урны взяли 1 белый 2 черных и вернули 1 белый 1 черный:

2

Рассмотрим третий случай. Пусть событие B3 — событие что из первой урны взяли 2 белых 1 черный и вернули 2 белых:

Тогда итоговой вероятностью того, что в первой урне окажется столько же белых шаров, сколько было изначально:

P(A) = P(B1A) + P(B2A) + P(B3A) = 0,0283 + 0,1485 + 0,0715 = 0,2483

Ответ: 0,2483

Задание 4. В лаборатории имеется 5 идентичных коплекта приборов, каждый из которых состоит из 6-ти приборов. Приборы работают независимо друг от друга. Вероятность выхода из сторя каждого прибора к концу срока эксплуатации 0.1. Определить вероятность того, что к концу срока эксплуатации из работающих приборов можно будет составить хоть один полный комплект.

Решение. По условию задачи нужно, чтобы к концу срока эксплуатации работающим был хотя бы один комплект, то есть от 6 до 30 приборов или же должно остаться целыми хотя бы 6 приборов. Пусть p = 1 − 0,1 = 0,9

P= 1 − ((1 − p)6)6

,где (1 − p)6 - вероятность поломки целого комплекта Подставив исходные значения, получим:

P = 1 − (0,000001)6 = 1 − (10−36) = 0,99999999999999999999999999999999999 (”0,” + 35 ”9”)

Ответ: 1 − (10−36) = 0,99999999999999999999999999999999999 (”0,” + 35 ”9”)

Задание 5. Вероятность успеха в схеме Бернулли равна 1/4. Проводится 2000 испытаний. Написать точную формулу и вычислить приближенно вероятность того, что число успехов попадает в интервал [471,529]

Решение.

Ответ: 0,8638

3