9.1 Проверка возможности возникновения автоколебаний методом гармонического баланса
Проверка проводится с помощью соотношения
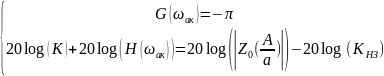
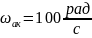
В
этой точке на графике ЛАЧХ строится
нормированный вектор 20lg(|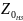
|),
начало которого смещено на -20lg(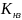
)
Запасы по амплитуде
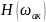=-26.239
дБ
=
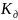=1
Если
,
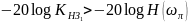то будет выполняться условие возникновения
автоколебаний.
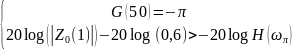
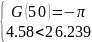
Условие баланса фаз выполняется, а условие баланса амплитуд — нет. Поэтому в системе автоколебаний не будет. Тогда найдем такое значение , чтобы выполнялись два условия
=-26.239 дБ
= =0.079
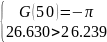
Теперь выполняются оба условия
А/а=1
Зона линейности
a=Xл=3(Xош)уст=3*0,53 мкс =1,56 мкс
Теперь рассчитаем предельные значения задающего воздействия
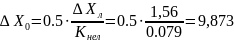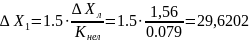В
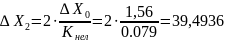В
В
10. Исследование режима срыва слежения в замкнутой нелинейной системе на лабораторной установке
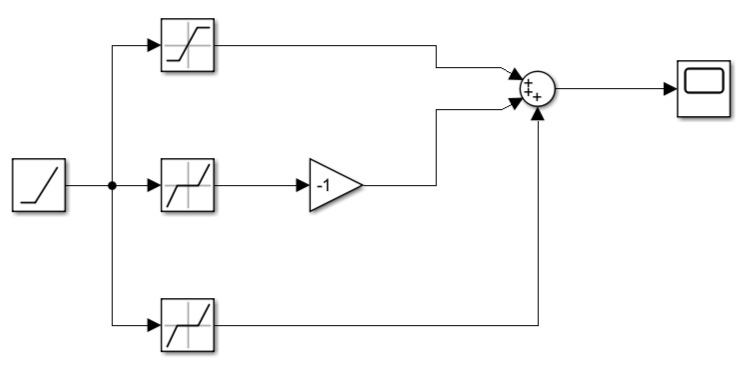
Рисунок 67 – Нелинейное звено системы
Рисунок 68 – Осциллограмма при подаче на нелинейное звено
линейно возрастающего воздействия
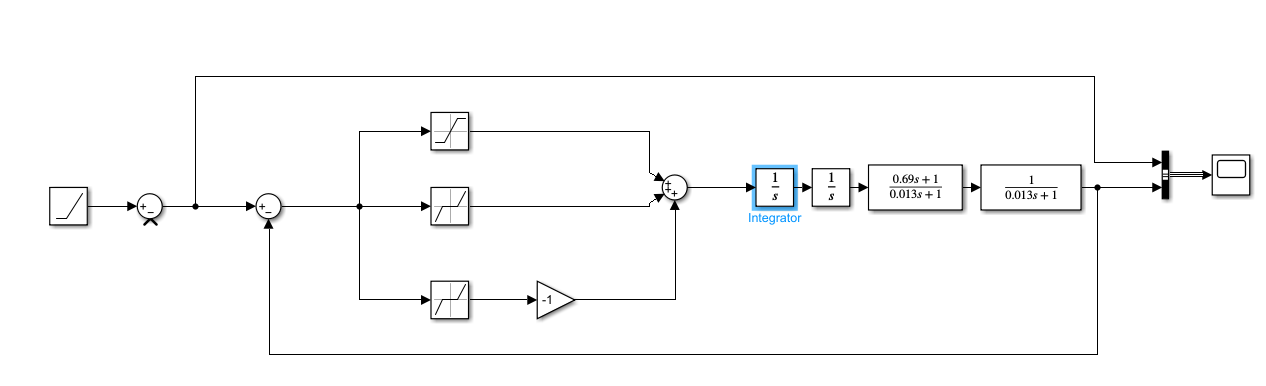
Рисунок 69 – Полная система при подаче линейно возрастающего воздействия
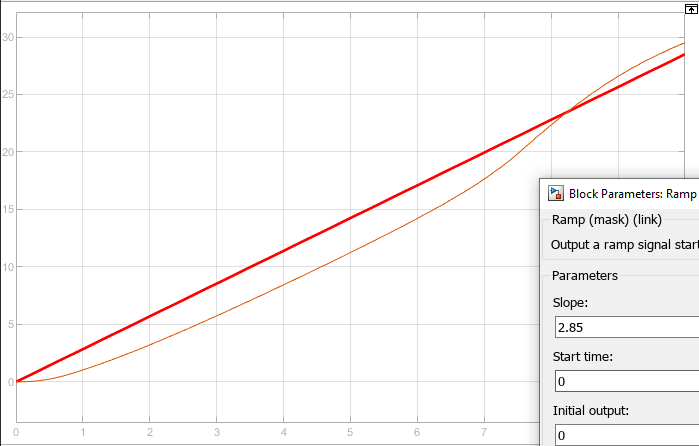
Рисунок 70 – Реакция системы на линейно возрастающее воздействие при 2.85
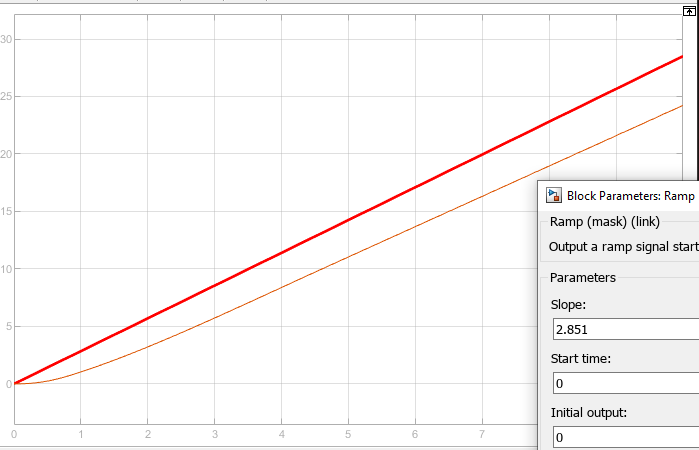
Рисунок 71 – Реакция системы на линейно возрастающее воздействие при 2.851
При значении 2.851 наблюдается срыв слежения
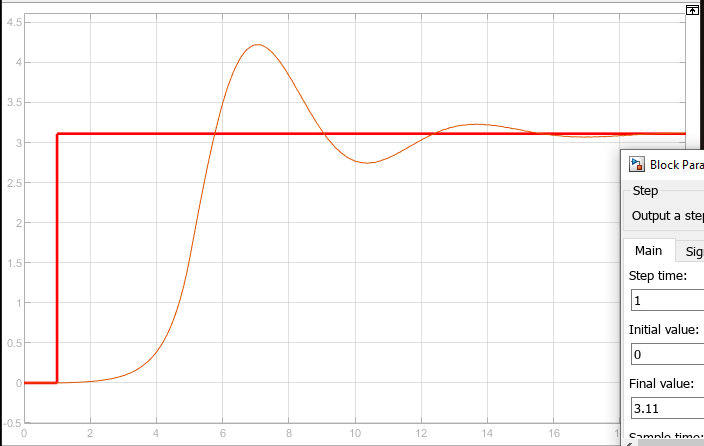
Рисунок 72 – Реакция системы на ступенчатое воздействие при 3.11
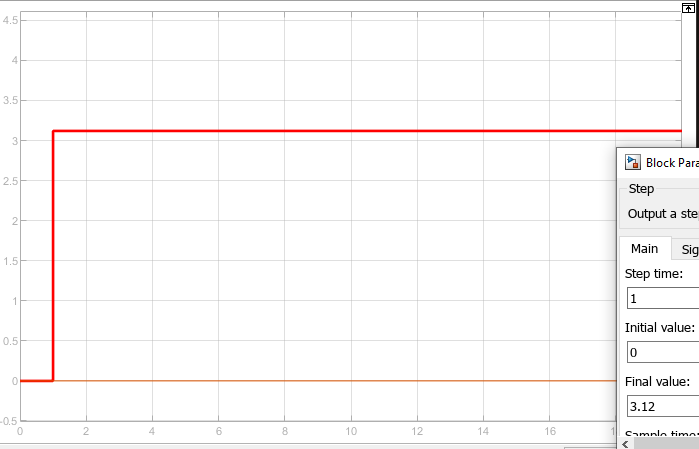
Рисунок 73 – Реакция системы на ступенчатое воздействие при 3.12
При подаче 3.12 наблюдается срыв слежения.
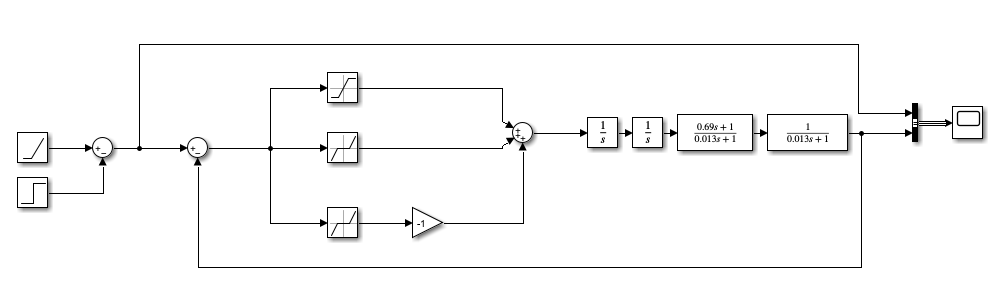
Рисунок 74 – Полная система при подаче суммарного воздействия
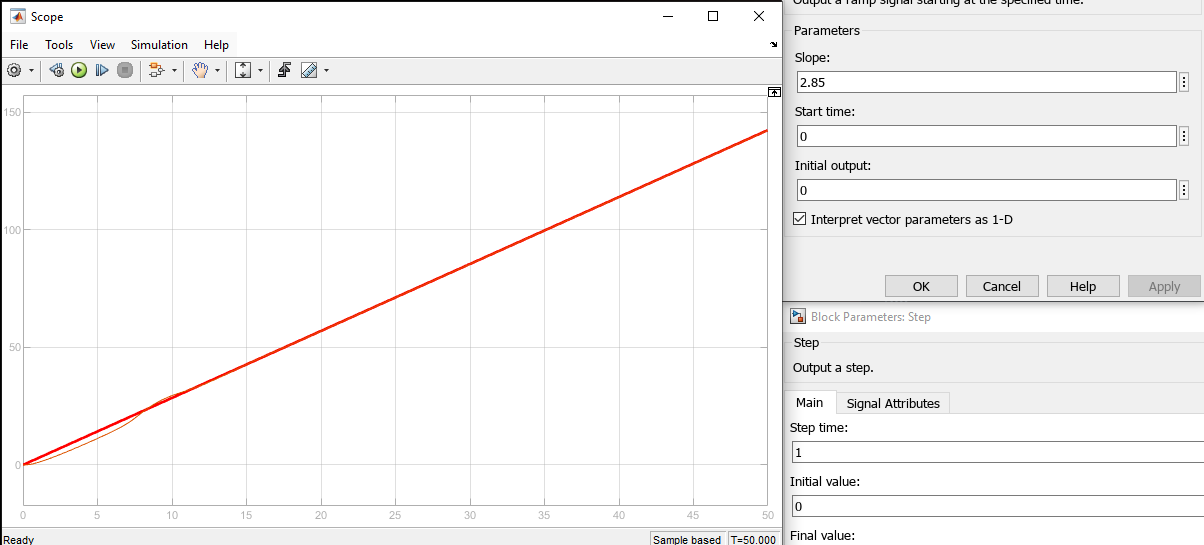
Рисунок 75 – Реакция системы на суммарное воздействие
при 2.85 и 0
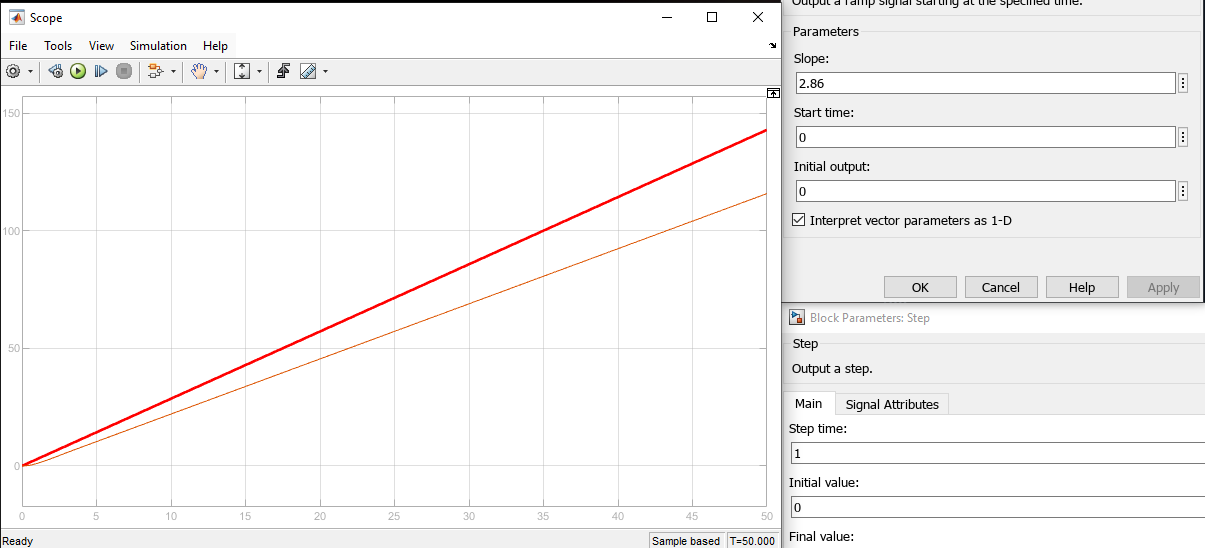
Рисунок 76 – Реакция системы на суммарное воздействие при 2.86 и 0
Вывод:
В ходе выполнения лабораторной работы были исследованы реакции цепей с включёнными нелинейностями на линейно нарастающее и ступенчатое входные воздействия. По результатам экспериментов можно сделать вывод, что максимальная амплитуда воздействия, при котором в системе не происходит срыва слежения в случае линейно нарастающего воздействия в разы больше, чем в случае ступенчатого. Так, для ступеньки величина амплитуды "срыва" составляет 1, в то время как для линии 6,5. Однако стоит отметить, что даже без срыва, реакция цепи на линейно нарастающее воздействие отклоняется всё дальше и дальше от самого воздействия. При комбинированном входном сигнале достигается некий оптимум, при котором на граничной амплитуде имеется некоторое отклонение в начале воздействия и почти полное совпадение графиков ближе к концу.
11. Преобразование исследуемой системы в импульсную путём добавления импульсного п-образного элемента; построение частотных и импульсных характеристик для полученной системы
Проведём разложение выражения желаемой системы на более простые дроби.
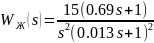
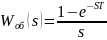
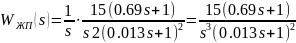
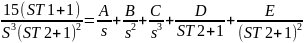
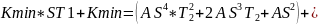
Выпишем все полученные коэффициенты:
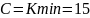
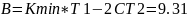
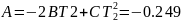
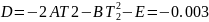
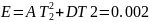
Воспользовавшись
таблицей преобразования W
находим для
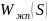преобразование:
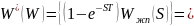
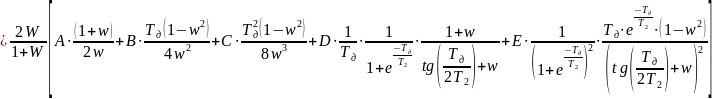
Используя математический пакет Mathcad, найдем корни в числителе.
;
;
;
;
;
;
;
;
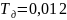
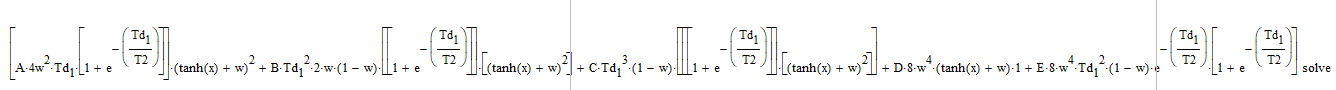
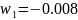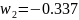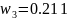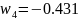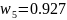
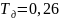
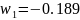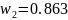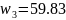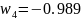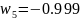
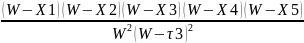
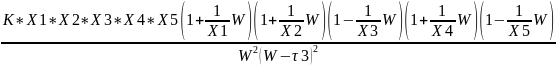
Построим графики ЛАЧХ и ЛФЧХ.
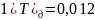
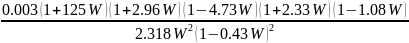
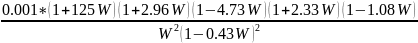
Рисунок 77 – ЛАЧХ и ЛФЧХ
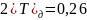
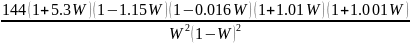
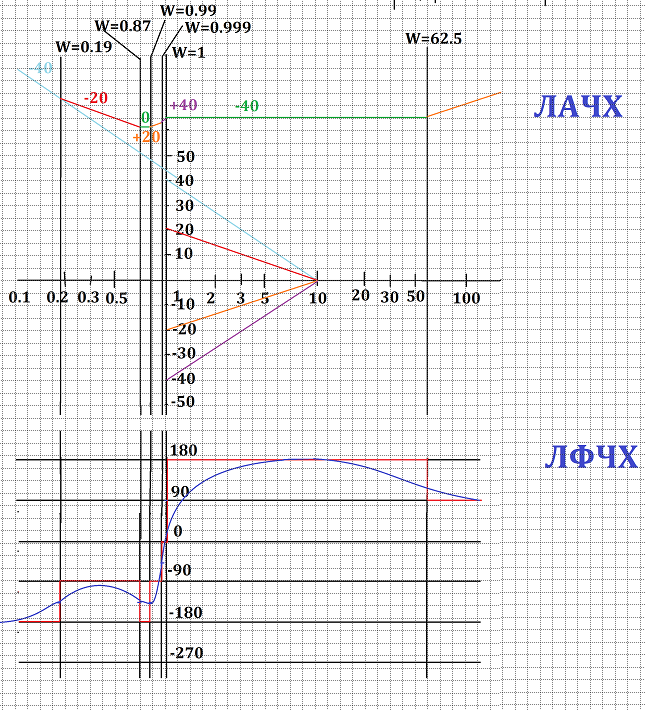
Рисунок 78 – ЛАЧХ и ЛФЧХ
Входное воздействие: единичный скачок:
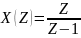
Воспользовавшись таблицей преобразования Z находим для преобразование:
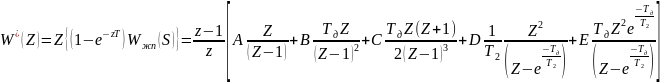
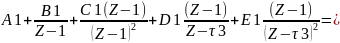
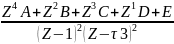
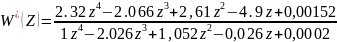
Рассчитаем установившуюся ошибку в замкнутой импульсной системе:
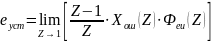
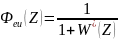
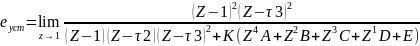
Значения ошибки для разных Тд:
Тд |
|
0,012 |
0 |
0,26 |
0 |
Рассчитаем переходный процесс и построим импульсную характеристику.
Tд |
n |
Коэффициент Сn |
0.012 |
0 1 2 3 4 |
0 2.732 0.72 -1.882 -0.819 |
0.26 |
0 1 2 3 4 |
0 5.652 11.288 8.583 4.713 |
Импульсные характеристики
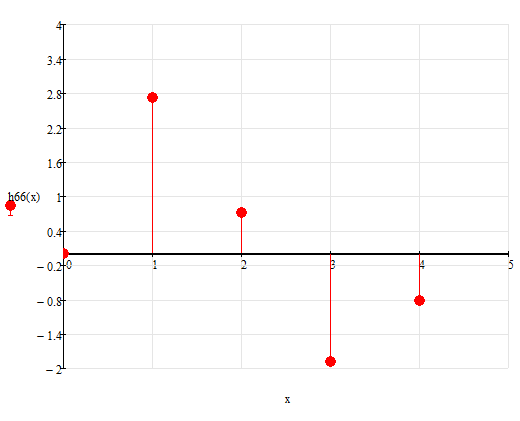Рисунок
79 – Импульсная характеристика для
Tд=0.012
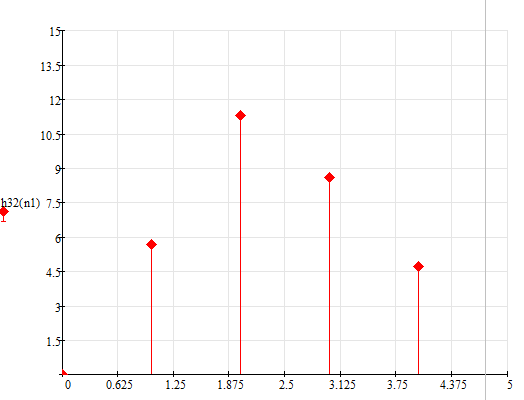
Рисунок 80 – Импульсная характеристика для Tд = 0.26
Вывод:
В данной курсовой работе было произведено ознакомление с основами проектироавния систем автоматического управления как с использованием расчетных и графоаналитических методов, так и с помощью систем автоматизированного проектирования для ЭВМ.
Было проведено ознакомление с назначением и особенностями проектируемой радиоавтоматической системы, были исследованы ее динамические свойства при заданных исходных параметрах элементов. Был произведен поиск подходящих значений параметров системы, при которых показатели качества работы системы, определяющие степень колебательности переходных процессов, точность и быстродействие, имеют требуемые значения при заданных уровнях и типах полезного воздействия Xвх в (t) и мешающих воздействиях Xм в(t). Также была осуществлена коррекция исходной системы с передаточной функцией Wн(S) путем включения в систему динамических звеньев коррекции с передаточной функцией Wкорр(S). Было исследовано влияние на работоспособность и динамические свойства скорректированной системы имеющихся в ее составе нелинейных звеньев. Было проведено исследование влияния дискретизации входного сигнала по времени, имеющего место в импульсных радиотехнических устройствах, на динамические свойства радиоавтоматических систем.
Москва 2024