
- •Исходные данные системы
- •Теоретические сведения об асн
- •2.4 Расчет интегрирующего звена c оос
- •2.5 Расчет первого инерционного звена c оос
- •2.6 Расчет второго инерционного звена c оос
- •3. Исследование временных характеристик звеньев первого порядка
- •4. Построение лачх, лфчх, афчх и определение запасы устойчивости по модулю и фазе
- •5. Исследование нескорректированной замкнутой системы
- •6. Расчёт и построение желаемого звена и звена коррекции; их характеристик
- •6.1 Расчет ошибки при детерминированных мешающих воздействиях, приложенных к выходу системы Хмв2(t):
- •6.2 Расчет ошибки при детерминированных мешающих воздействиях, приложенных к выходу дискриминатора Хмв1(t):
- •6.3 Расчет среднеквадратического значения флуктуационной составляющей ошибки:
- •7. Замкнутая скорректированная система на лабораторной установке
- •8. Скорректированная система после включения в нее нелинейного звена
- •9.1 Проверка возможности возникновения автоколебаний методом гармонического баланса
- •10. Исследование режима срыва слежения в замкнутой нелинейной системе на лабораторной установке
- •11. Преобразование исследуемой системы в импульсную путём добавления импульсного п-образного элемента; построение частотных и импульсных характеристик для полученной системы
4. Построение лачх, лфчх, афчх и определение запасы устойчивости по модулю и фазе
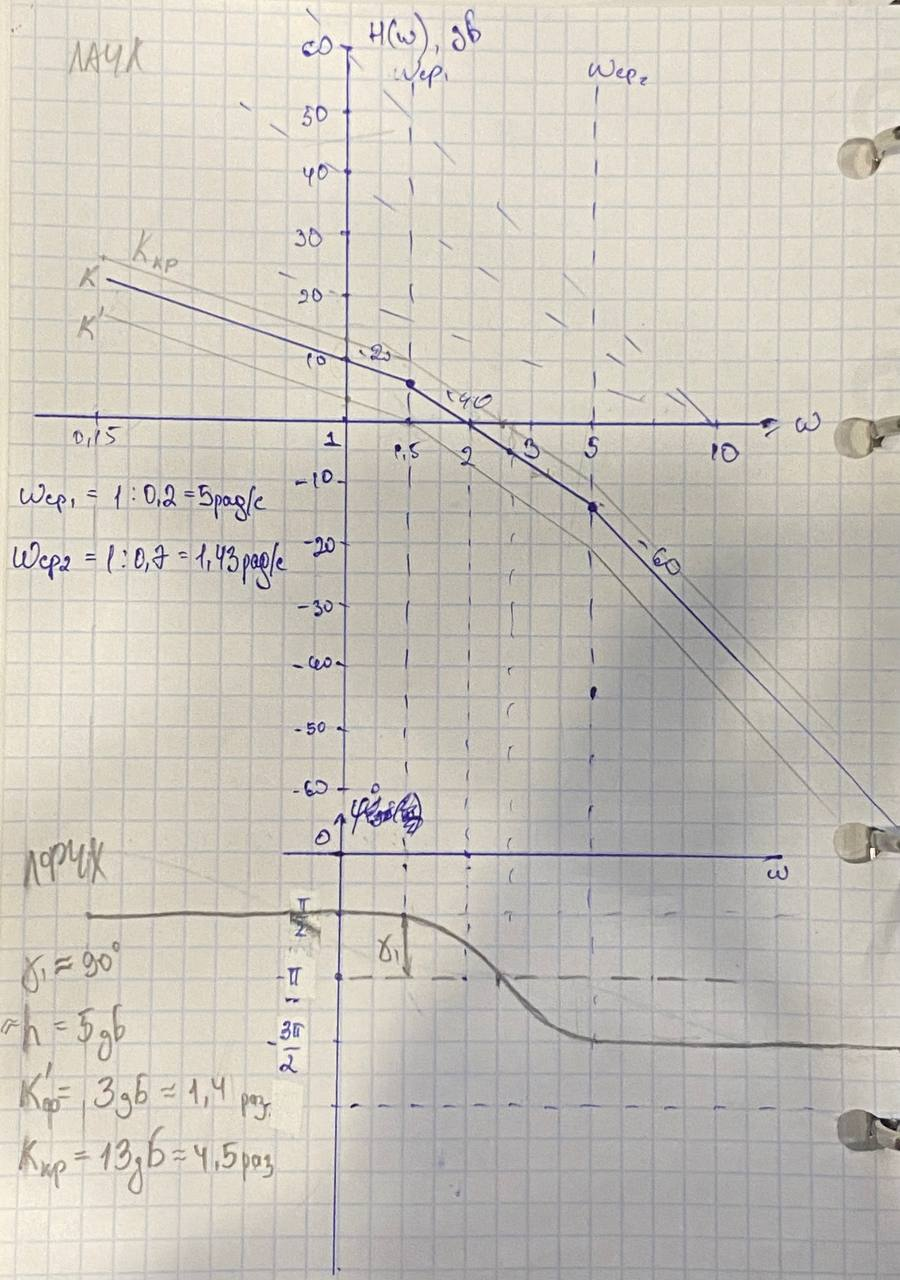
Рисунок 31 – ЛАЧХ и ЛФЧХ
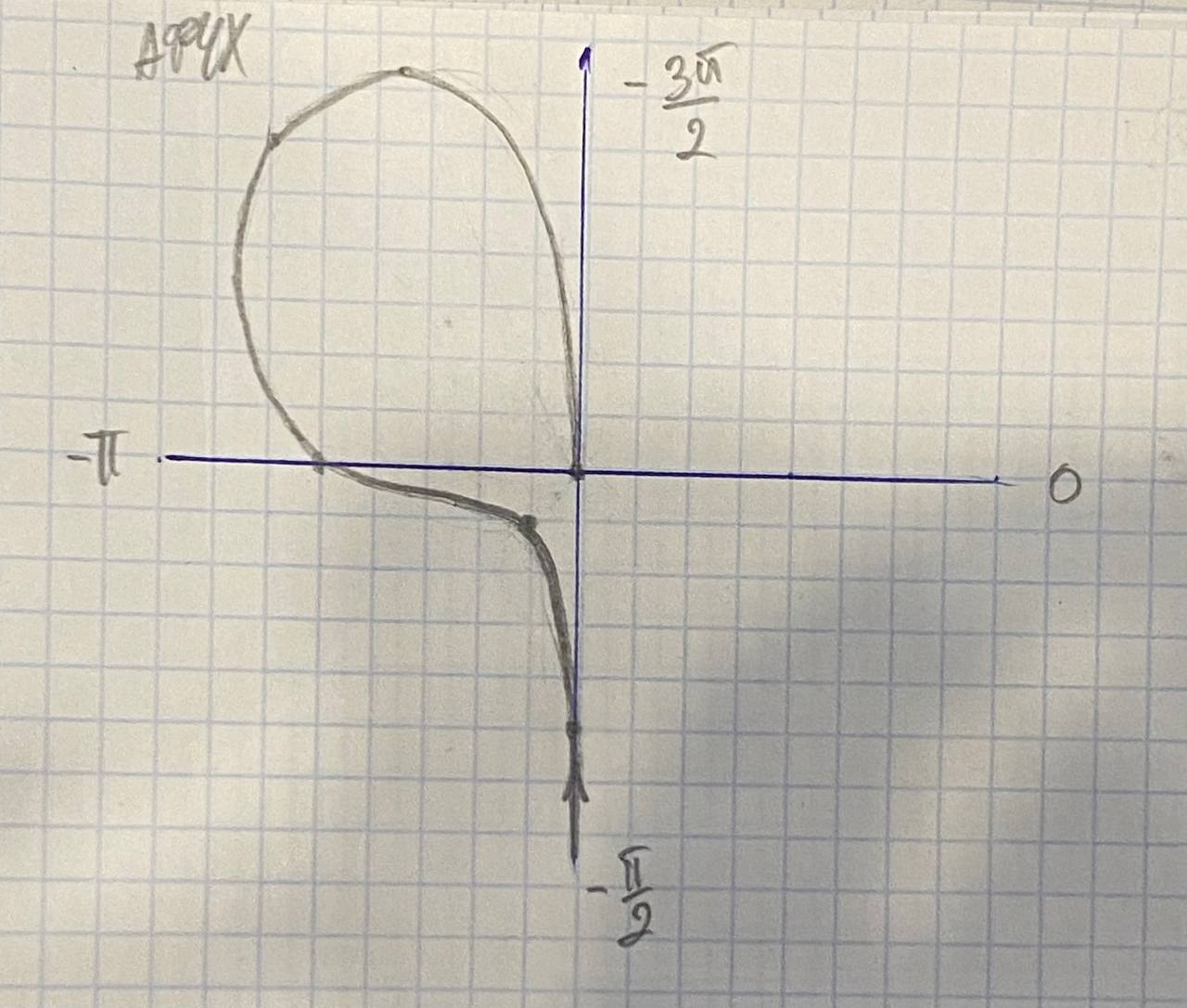
Рисунок 32 – АФЧХ
5. Исследование нескорректированной замкнутой системы
Построим ЛАЧХ, ЛФЧХ, АФЧХ для замкнутой системы в программе Matlab Simulink.
Возьмем коэффициенты усиления:
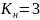
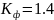
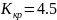
При Кн=3
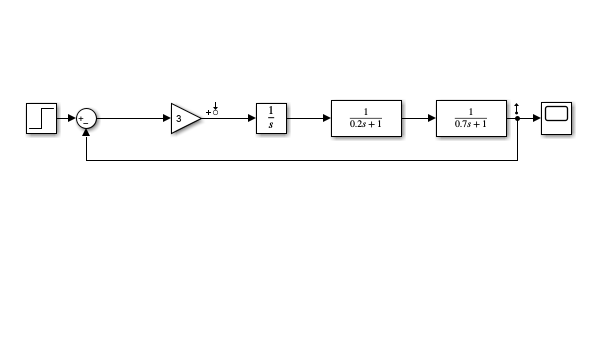
Рисунок 33 – Схема системы при Кн
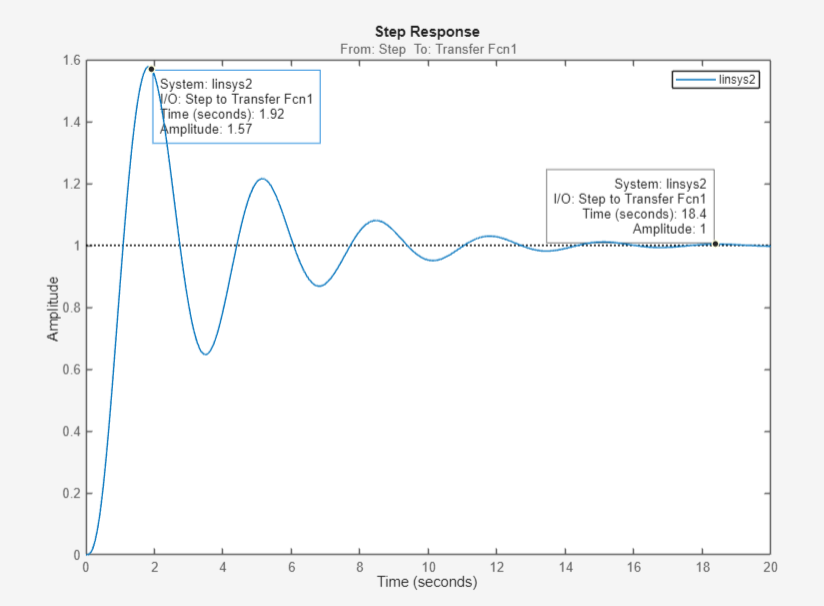
Рисунок 34 – Переходная характеристика системы при Кн
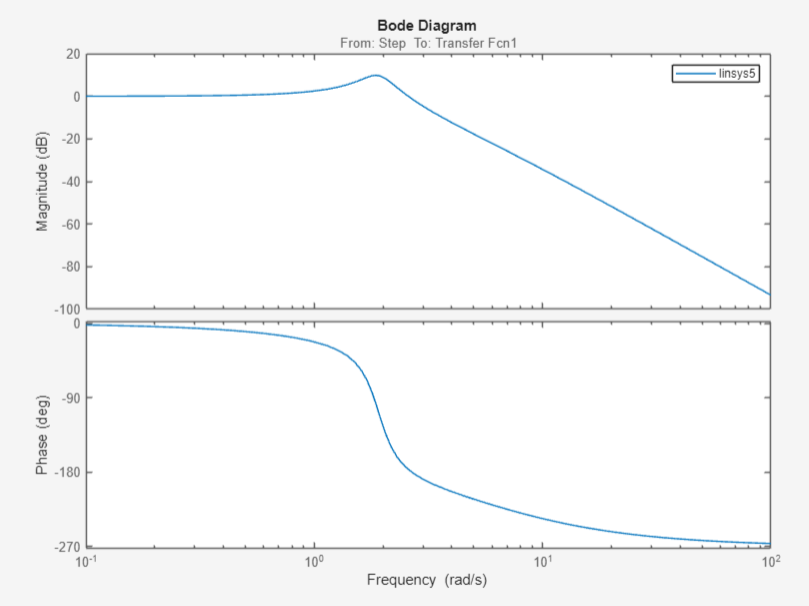
Рисунок 35 – ЛАЧХ и ЛФЧХ системы при Кн

Рисунок 36 – АФЧХ системы при Кн
При Кф=1.4

Рисунок 37 – Схема системы при Кф
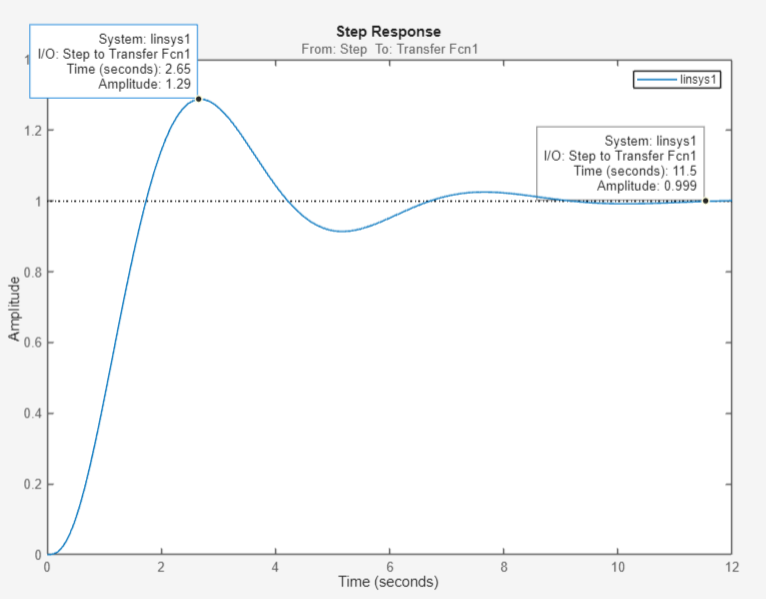
Рисунок 38 – Переходная характеристика системы при Кф
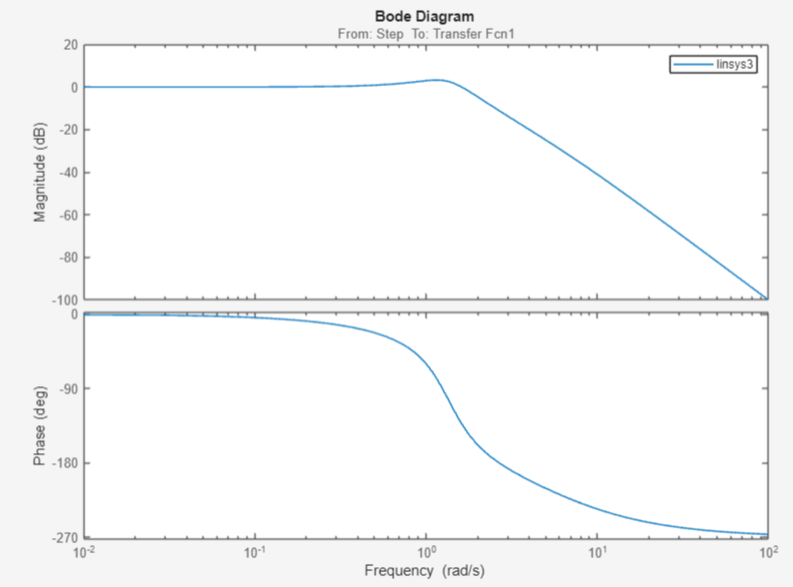
Рисунок 39 – ЛАЧХ и ЛФЧХ системы при Кф
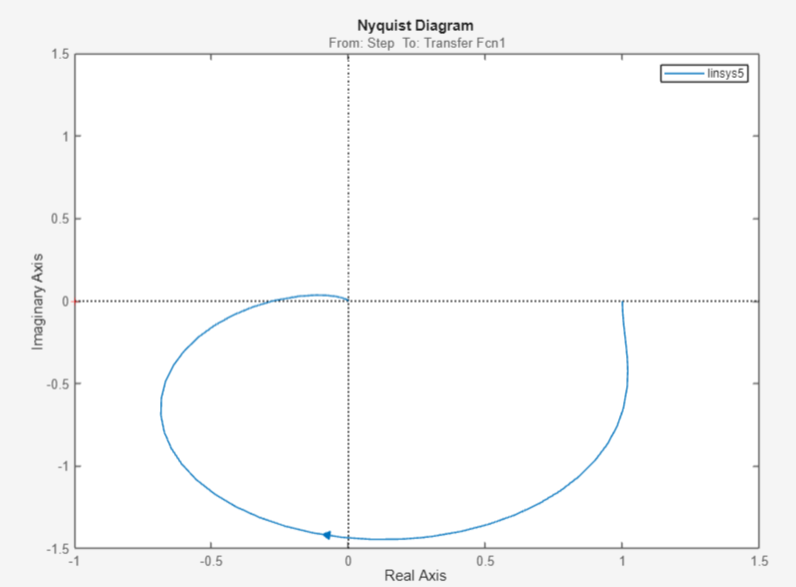
Рисунок 40 – АФЧХ системы при Кф
При Ккр=4.5
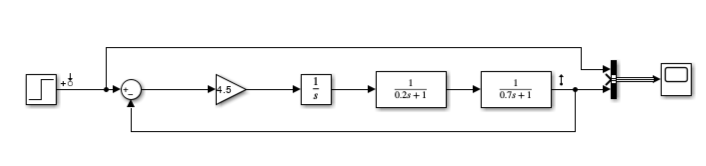
Рисунок 41 – Схема системы при Ккр
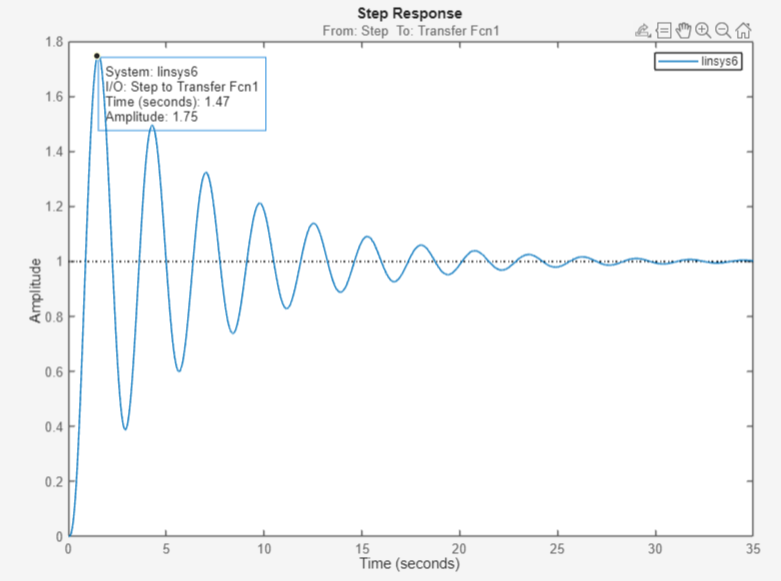
Рисунок 42 – Переходная характеристика системы при Ккр
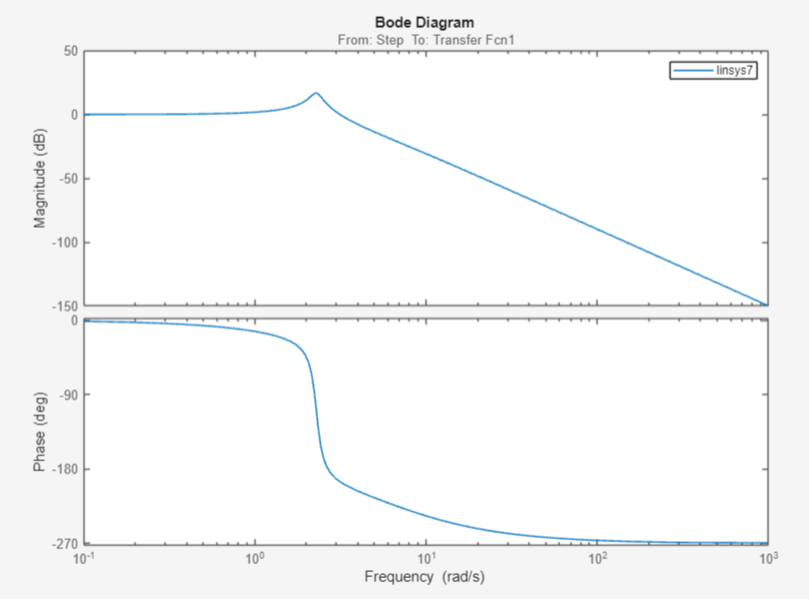
Рисунок 43 – ЛАЧХ и ЛФЧХ системы при Ккр

Рисунок 44 – АФЧХ системы при Ккр
K |
Kф |
Kн |
Kкр |
Значение |
1.4 |
3 |
4.5 |
σ % |
30 |
57 |
75 |
Tуст, с |
12 |
19 |
35 |
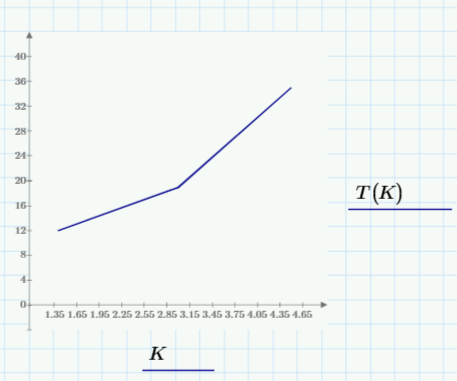
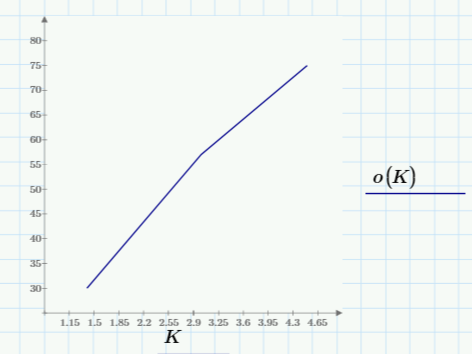
Рисунок 45 – Зависимость Ту(К) и σ%(К)
Вывод:
В ходе выполнения лабораторного практикума были получены графики ЛАЧХ, ЛФЧХ и годограф нескорректированной цепи динамических звеньев, так же была получена зависимость времени установления импульса и перерегулирования в системе от коэффициента усиления интегрирующего звена. По полученным графикам можно сделать вывод, что при увеличении коэффициента усиления К увеличивается перерегулирование и время установления импульса в системе.
6. Расчёт и построение желаемого звена и звена коррекции; их характеристик
Вид САР |
W(S) неизменяемой части САР |
Kд |
Kн |
РТ-62 постоянные времени |
Xвх(t) |
|||||
В/град |
1/с |
Ty3 |
Tан |
град |
||||||
АСД |
|
1 |
12 |
0.2 |
0.7 |
8 |
||||
(Xош)уст от Xвх(t) |
Ty |
Xмв1 |
Xмв2 |
S()=S0 |
||||||
мкс |
с |
В |
мкс |
В2/Гц |
||||||
1 |
1 |
0.035 |
4 |
4*10-3 |
||||||
Xвх(t)=8 град/с=8*t2
Порядок астатизма v=2, т.к производная входного воздействия равна 2
Минимальный коэффициент усиления:
Kmin=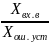 =
=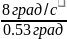 =
= 1/с
1/с
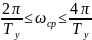
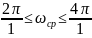
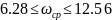
Пусть
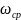 =
10 рад/с
=
10 рад/с
Kmin дБ=20*log(Kmin)=23.5 дБ
Параметры желаемой системы:
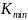 =
15
=
15
= 10
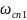 =
1.438
=
1.438
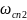 =
80
=
80
 =
0.69
=
0.69
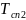 =
0.013
=
0.013
Передаточная функция желаемой системы
 =
=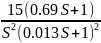
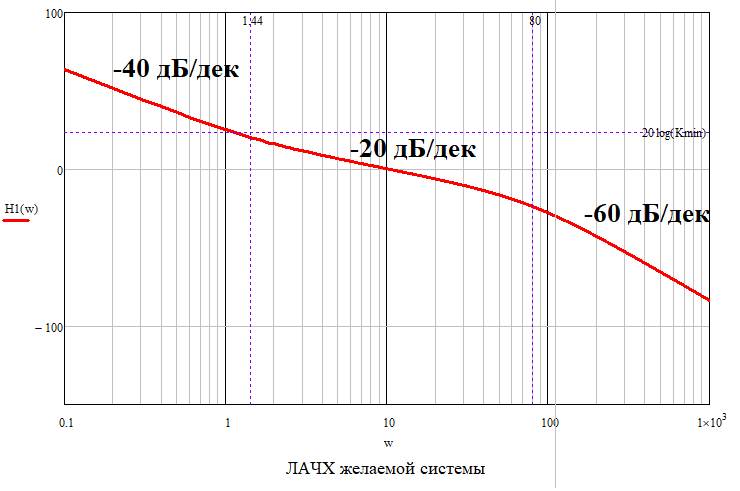
Рисунок 46 – ЛАЧХ желаемой системы

Рисунок 47 – ЛФЧХ желаемой системы
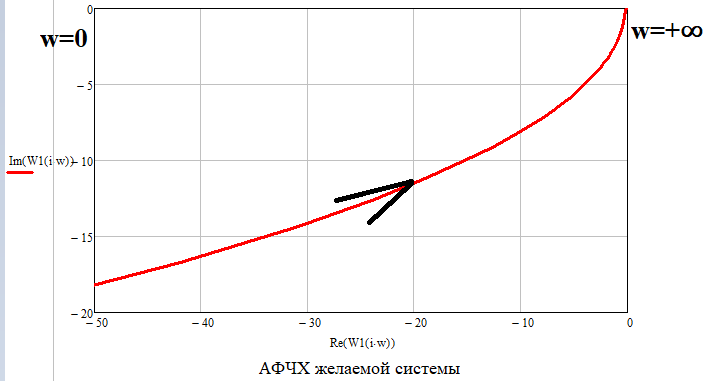
Рисунок 48 – АФЧХ желаемой системы
Корректирующее звено:
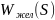 =
=
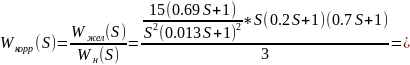
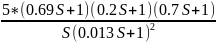
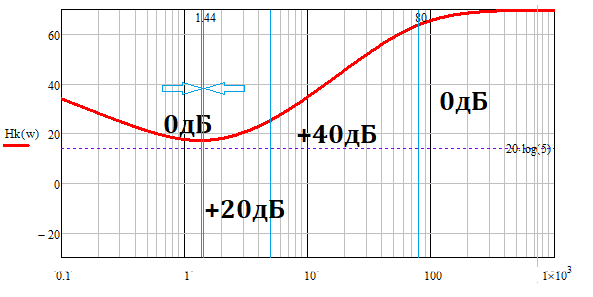
Рисунок 49 – ЛАЧХ желаемой системы
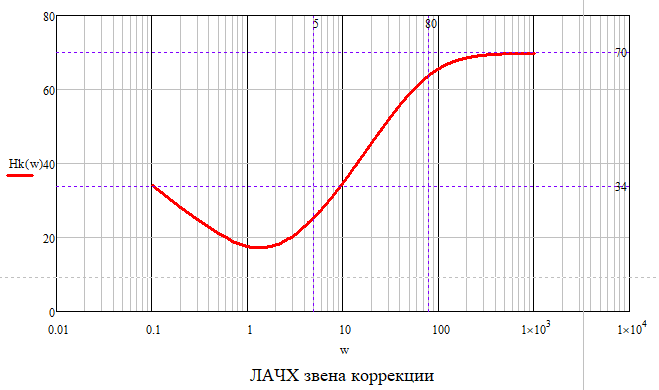
Рисунок 50 – ЛАЧХ звена коррекции

Рисунок 51 – ЛФЧХ желаемой системы
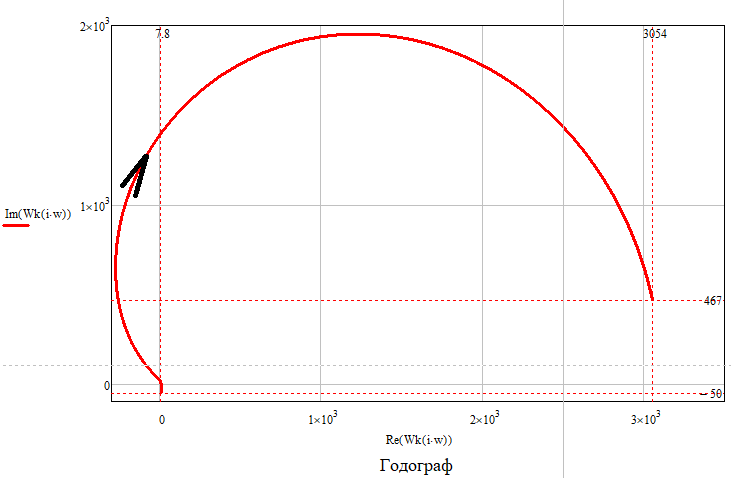
Рисунок 52 – АФЧХ желаемой системы
6.1 Расчет ошибки при детерминированных мешающих воздействиях, приложенных к выходу системы Хмв2(t):
eуст.=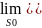 *X(S)*Фвu(S))
*X(S)*Фвu(S))
— обобщенный вид формулы ошибки при детерминированных мешающих воздействиях
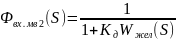 =
=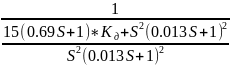 =
=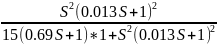
X мв2(t)=4*1(t)
Переведем в частотную область
X
мв1(S)=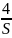
eмв2= *Xмв2(S)*Фвх.мв2(S))
eмв2=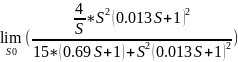 =0
В
=0
В
Переведем во временную область
eуст.мв2=0 мкс

