Методические указания радиоавтоматика

г) сравнить результаты расчёта и эксперимента.

Для выполнения данного пункта необходимо:

1) собрать систему по варианту из блоков в Simulink.

Рис. 3.5 Модель нескорректированной замкнутой системы.

Для ввода значений параметров системы по варианту, открыть окно инерционного звена. Ввести значение коэффициента усиления в строке Numerator, значение множителя перед s - первая цифра в строке Denominatior, значение коэффициента запаздывания - вторая цифра в строке Denominatior.

21

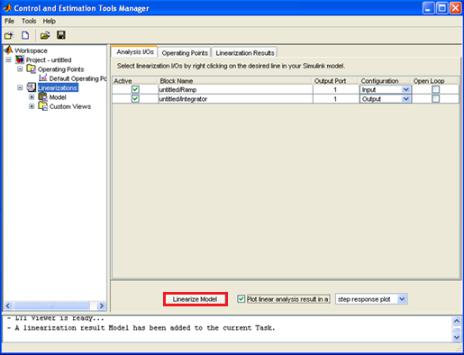
Рис. 3.6 Окно параметров инерционного звена

2) повторить действия, описанные в пункте 4 задания, заменив единичное звено собранной системой. Также можно получить ЛАЧХ, ЛФЧХ, АФЧХ системы.

На входе системы динамических звеньев кликнуть правой кнопкой мыши по соединительной линии и выбрать в выпадающем меню linearizationpoint → Inputpoint. На выходе системы динамических звеньев выбрать Outputpoint. В командной строке окна модели выбрать вкладку Tools и активизировать дополнительную программу LinearAnalysis(Controldesign→ LinearAnalysis). Появится окно Model_inputs_and_outputs.

Рис. 3.7 Окно программыLinearAnalysis

Вэтом окне инициируйте опцию Leniarized Model. Появится график. Чтобы получить частотные характеристики, необходимо использовать опцию Plot Configurations меню Edit. В открывшемся окне выбрать виды графиков и способы их размещения. Достаточно выбрать АЧХ, ФЧХ (Bode) и АФЧХ

(Nyquist diagram).

ВАФЧХ (Nyquist diagram) при выведении графика на экран, появляется изображение и для отрицательной области частот. Для того чтобы от него избавиться, необходимо правой кнопкой мыши щелкнуть в область графика, в меню выбрать «Show», снять галочку с «Negative Frequencies».

22

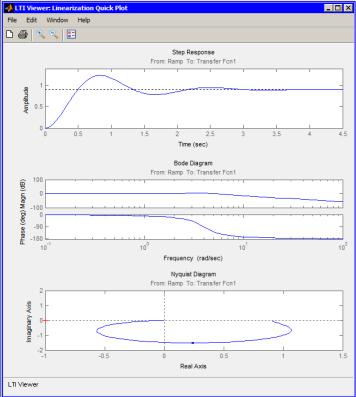
Рис. 3.8 ЛАЧХ ЛФЧХ и АФЧХ для замкнутой нескорректированной системы

7. а) определить минимально допустимые величины порядка астатизма системы относительно задающего воздействия по варианту и ее коэффициента усиления , а также частоту среза, обеспечивающие заданные показатели качества;

б) построить желаемые ЛАЧХ, ЛФЧХ, АФЧХ системы обеспечивающей перерегулирование σ% не более 30%, заданную точность и заданное быстродействие;

в) выбрать параметры звена коррекции и построить его ЛАЧХ, ЛФЧХ,АФЧХ;

г) записать передаточную функцию звена коррекции;

д) изобразить блок-схему системы после коррекции;

е) представить передаточную функцию скорректированной системы в форме, удобной для набора ее на лабораторной установке;

Примечания:

1.Коррекция систем по всем вариантам должна обеспечиваться простейшими звеньями и средствами.

2.По согласованию с ведущим преподавателем может быть использован любой вид и способ коррекции, отличный от указанного в задании.

23

3. При всех видах коррекции порядок характеризующего уравнения должен быть не более 4-х, а число форсирующих звеньев не более 2-х.

ж) рассчитать значения ошибок при детерминированных мешающих воздействиях, приложенных к выходу системы Хмв2(t) и к выходу дискриминатора Хмв1(t)

з) рассчитать суммарную ошибку от всех детерминированных воздействий, включая задающие;

и) рассчитать ср. кв. значение флуктуационной составляющей ошибки, вызванные шумами;

к) составить схему набора системы на лабораторной установке с указанием подключения мешающего воздействия Хмв2(t) при Хвх. в(t)=0.

8. Набрать на лабораторной установке замкнутую скорректированную систему и:

а) исследовать переходную характеристику системы при ступенчатом задающем воздействии, и определить σ%, Ту скорректированной системы;

б) попробовать улучшить качество переходного процесса в системе, несколько изменяя параметры звена коррекции;

в) оценить значение установившихся ошибок, и получить переходные характеристики при реакции скорректированной системы на ступенчатое, а затем, линейно меняющееся задающие воздействия;

г) оценить значения установившихся ошибок и получить переходные характеристики сигналов ошибок при ступенчатом и линейно меняющемся мешающих воздействиях Хмв2(t) при Хвх. в (t)=0;

д) сравнить полученные результаты с расчетными.

Для выполнения данного пункта необходимо:

а), б), в) повторить действия, описанные в пункте 6 задания, заменив систему по варианту скорректированной системой. А так же подключив дополнительный осциллограф, для снятия ошибки между блоком Sum и первым блоком системы.

24

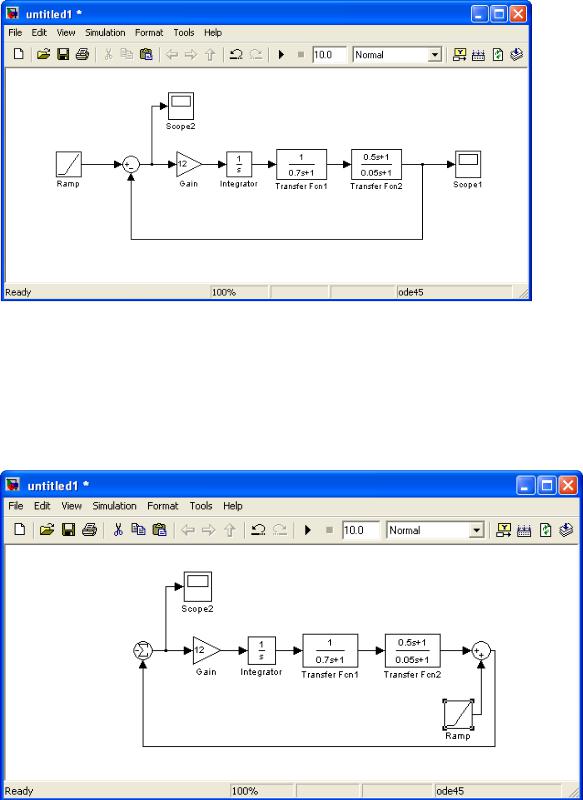
Рис. 3.9 Модель скорректированной замкнутой системы.

г) – собрать скорректированную систему. На выходе системы поставить блок Sum и подключить к нему блок Step, либо блок Ramp (мешающее воздействие). Далее охватить получившуюся конструкцию ООС. Подключить осциллограф между блоком Sum, использованным для создания ООС и первым блоком системы.

Рис. 3.10 Модель скорректированной системы с мешающим воздействием.

9. Рассматривая скорректированную систему по варианту после включения в нее нелинейного звена как непрерывную и нелинейную:

а) рассчитать и построить эквивалентные нормированные коэффициенты передачи Io(A/ao) и Zo=1/ Io(A/ao) для нелинейного звена НЗ1 с S-образной тре-

25

угольной характеристикой и нелинейного звена НЗ2 – звена с линейной зоной и насыщением;

б) проверить методом гармонического баланса, используя логарифмическую плоскость, возможно ли возникновение автоколебаний в нелинейной системе по варианту, а если при параметрах желаемой системы автоколебания невозможны, то указать минимально возможный коэффициент усиления скорректированной системы или Кна, при котором они возможны;

в) рассчитать для системы с S-образной треугольной характеристикой предельные значения задающего воздействия

ному значению установившейся ошибки [(ΔXoш)уст]пред= Xα полагая, что зо-

на линейности X л равна утроенной допустимой установившейся ошибки, в приведенной в индивидуальном задании;

г) составить схему набора нелинейных звеньев НЗ1 и НЗ2 по п.а.;

д) составить общую схему набора всей нелинейной системы с нелинейным звеном НЗ1 и скорректированной линейной частью.

10. Исследовать на лабораторной установке режим срыва слежения в замкнутой нелинейной системе по варианту и:

а) получить S-образную статическую характеристику нелинейной части;

б) собрать на лабораторной установке полную замкнутую систему с нелинейной частью;

в) подавая на вход системы линейно возрастающее и ступенчатое воздействия, а так же их сумму, определить границы рабочей зоны системы;

г) изучить фазовый портрет системы.

Для выполнения данного пункта необходимо:

1) Используя библиотеку Discontinuities и блок Sum собрать необходимую нелинейность из блоков Saturation и Dead Zone. В блоке Saturation необходимо задать верхние и нижние пределы в полях Upper limit и Lower limit. В блоке Dead Zone – начало и конец зоны в полях Start of dead zone и End of dead zone;

26

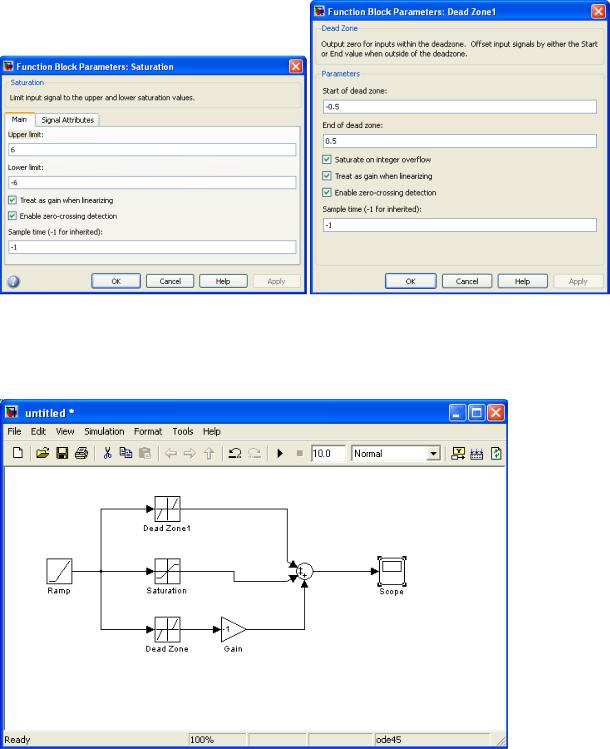
Рис. 3.11 Свойства блоков Saturation и Dead Zone

2) подав на вход линейно возрастающее воздействие и подключив осциллограф наблюдать статическую характеристику;

Рис. 3.12 Собранная нелинейность

27

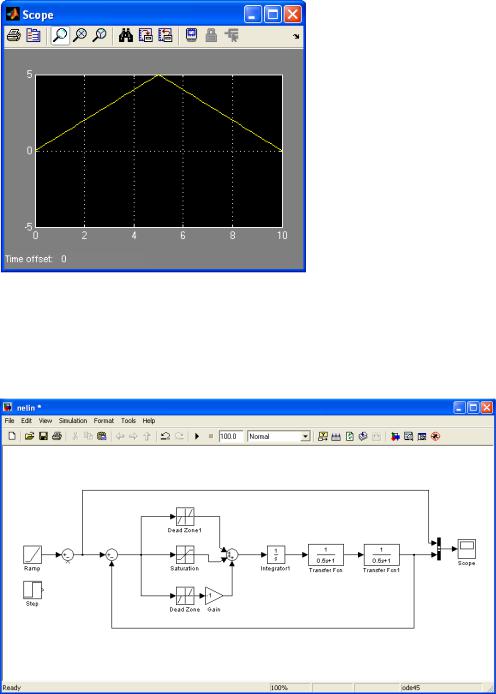
Рис. 3.13 Осциллограмма при подаче на нелинейность линейно возрастающего воздействия

3) собрать полную замкнутую систему с нелинейной частью, по аналогии с предыдущими пунктами;

Рис. 3.14 Вид модели полной системы

4)подавая на вход линейное воздействие и увеличивая параметр Slope добиться срыва слежения;

5)подавая на вход ступенчатое воздействие и увеличивая параметр Final Value добиться срыва слежения;

6)подавая на вход сумму линейного и ступенчатого воздействий и увеличивая параметры Slope и Final Value добиться срыва слежения;

7)используя Matlab открыть программу Fazovyi_portret;

28

8) ввести в программе свои значения коэффициента усиления и постоянных времени. Так же ввести нижний и верхний пределы рабочей зоны, изменив значения х0_min и x0_max;

9) в строках программы «open_system ('model.mdl')» и «sim ('model')» вве-

сти названия файла модели, соответствующего скорректированной системе.

Таблица 3.1.

10) Запустить программу и изучить фазовый портрет системы. В случае, если фазовый портрет изображен в неявном виде, возможно изменение значений шага dx и dy.

29

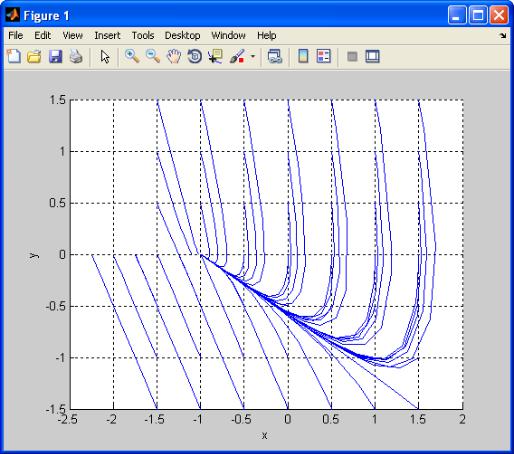
Рис. 3.15 Вид фазового портрета системы

11. Составить импульсную систему, путём добавления к скорректированной системе импульсного П-образного элемента:

а) Воспользоваться программой «Расчет времени дискретизации» и выбрать три ТД из рекомендованных значений.

Примечания: значения постоянных времени вводятся в виде: 0,7. Если в системе есть только Т1 или Т1 и Т2, то остальные поля можно оставить пустыми.

б) Произвести Z- иWпреобразования скорректированной системы для трех

значений ТД с добавлением П-образного (1 e ST )элемента, используя таблицу:

30