Методические указания радиоавтоматика

Назначение: определение передаточной функции дискретного блока с заданными полюсами и нулями.

Параметры:

1.Zeros – вектор или матрица нулей;

2.Poles – вектор полюсов;

3.Gain – скалярный или векторный коэффициент передаточной функции;

4.Sample time — шаг дискретизации по времени.

5. Discontinuities – нелинейные блоки.

а. saturation - блок ограничения

Назначение: ограничение величины сигнала.

Параметры:

1.Upper limit – верхний порог ограничения;

2.Lower limit – нижний порог ограничения;

3.Treatas gain when linearizing (флажок) – трактовать как усилитель с коэффициентом передачи равным 1 при линеаризации.

б. Dead Zone - блок с зоной нечувствительности

Назначение: реализация нелинейной зависимости типа "зона нечувствительности (мертвая зона)".

Параметры:

61

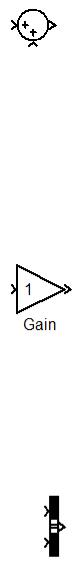
1.Start of deadzone – начало зоны нечувствительности (нижний порог);

2.End of deadzone – конец зоны нечувствительности (верхний порог);

3.Saturateon integer over flow (флажок) – подавлять переполнение целого. При установленном флажке ограничение сигналов целого типа выполняется корректно;

4.Treatas gain when linearizing (флажок) – трактовать как усилитель с коэффициентом передачи равным 1 при линеаризации.

6. Math operations – математические операции.

а. Sum – блок суммирования

Назначение: вычисление суммы текущих значений сигналов.

Параметры:

1.Icon shape – форма блока;

2.List of sign – список знаков;

3.Saturate on integer overflow (флажок) –подавлять переполнение целого.

б. gain– усилитель

Назначение: умножение входного сигнала на постоянный коэффициент.

7. Signal routing –блоки маршрутизациисигналов.

а. Bus creator – блок шинного формирователя.

Назначение: Формирование шины из сигналов различных типов.

Параметры:

1.Signal naming options – способ именования сигнала;

2.Number of inputs ports – количество входных портов;

62

3.Signal sin bus – список сигналов, объединяемых в шину;

4.Rename selected signal – новое имя выделенного сигнала. Параметр до-

ступен, если выбрана опция Require input signal names to match signals below.

8.Additionallinear – дополнительные линейные блоки библиотеки Simulink extrtas.

а. Zero-pole (with initial output) – блок передаточной функции с инициализацией выхода.

Назначение: определение передаточной функции с заданными полюсами и нулями. В этом блоке можно задавать начальные условия.

Параметры:

1.Zeros – вектор или матрица нулей;

2.Poles – вектор полюсов;

3.Gain – скалярный или векторный коэффициент передаточной функции;

4.Initial Output – задание значение сигнала на выходе блока в первый момент времени;

5.Initial Input – задание значение сигнала на входе блока в первый момент времени.

б. Transfer fcn (with initial output)- блок инерционного звена с инициализацией выхода.

Назначение: задание передаточной функции инерционного звена. В этом блоке можно задавать начальные условия.

Параметры:

1.Numerator —коэффициент числителя;

2.Denominator — коэффициенты знаменателя;

63

3.Initial Output – задание значение сигнала на выходе блока в первый момент времени;

4.Initial Input - задание значение сигнала на входе блока в первый момент времени.

Приложение 3. Исследование нелинейных систем. Краткие теоретические сведения о методе фазовых портретов.

Нелинейной называют систему, описываемую нелинейным дифференциальным уравнением. Обычно система является нелинейной вследствие наличия в ней одного или нескольких звеньев, описываемых нелинейным дифференциальным уравнением или имеющим нелинейную статическую характеристику. При этом система может иметь в своем составе линейные или линеаризованные обычными методами звенья.

Нелинейным считают такое звено, которое не поддается линеаризации в том смысле, что отказ от учета его нелинейных свойств существенно искажает результаты последующего анализа и делает их неприемлемыми.

Нелинейные звенья могут входить в состав автоматической системы вследствие неизбежности применения тех или иных технических устройств, но могут быть случаи, когда нелинейные зависимости специально вводятся в

систему для получения каких-либо желаемых ее свойств.

Одним из характерных видов нелинейных статических характеристик звена x2 F (x1 ) , где x1 и x2 - входная и выходная величины, являются ха-

рактеристики релейного типа (рис. П.3.1). Они присущи часто используемым в автоматических системах реле различных типов (электронные, электрические, пневматические, механические и др.)

Рис. П.3.1 Двухпозиционное реле

64

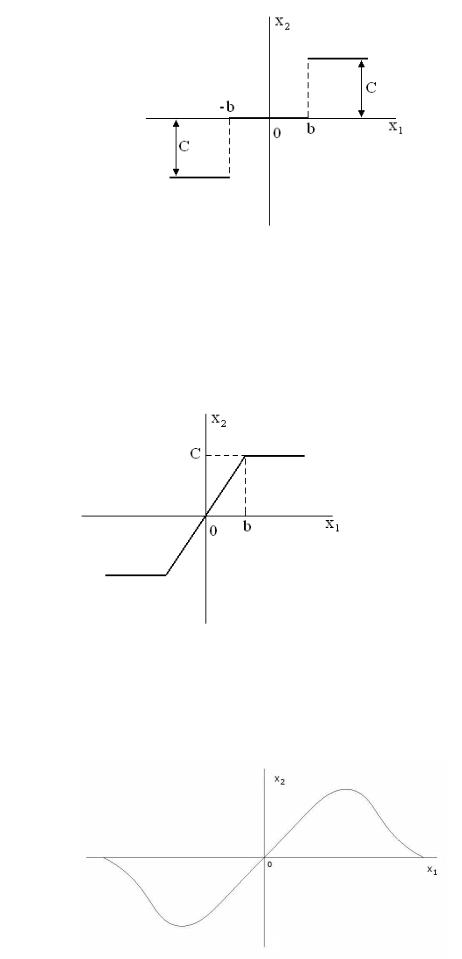
Рис. П.3.2 Трёхпозиционное реле

Характеристика на рис. П.3.1 относятся к двухпозиционному реле (имеет два устойчивых положения). Характеристика на рис. П.3.2 относятся к трехпозиционному реле.

Нелинейная статическая характеристика может иметь непрерывный

вид.

Рис. П.3.3 Звено с насыщением

Характеристика на рис. П.3.3 соответствуют ограниченно линейному звену с насыщением. Такие характеристики имеют, как правило, все усилители. Характеристики, подобные изображённой на рис. П. 3. 4, встречаются в различного рода дискриминаторах.

65

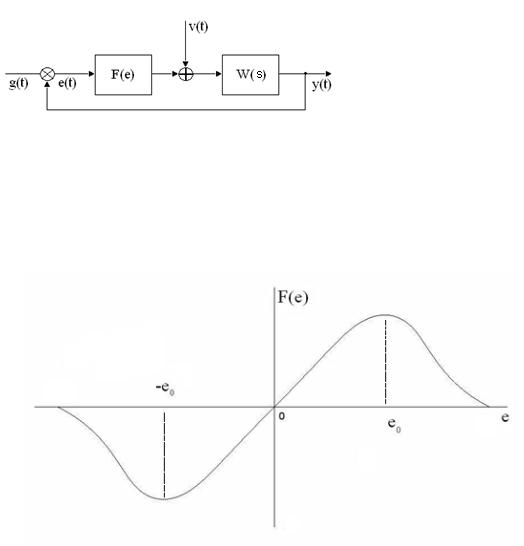
Рис. П.3.4 Стандартная характеристика дискриминатора

Внелинейных автоматических системах процессы имеют особенности, которые не встречаются в линейных системах.

Внелинейных системах неприменим принцип суперпозиции, который позволяет в линейных системах определять выходную величину как сумму составляющих, вызываемых действием различных факторов (задающего воздействия, возмущающих воздействий, помех). Выходная величина при наличии различных воздействий должна определяться для всех воздействий

всовокупности.

Понятие устойчивости в нелинейных системах оказывается более сложным. Возможно, что начальные значения или наблюдаемые в автоматической системе отклонения будут влиять на устойчивость. Так, может оказаться, что для «малых», т. е. не превосходящих некоторых значений отклонений или начальных значений, система будет устойчивой, а для «больших», т. е. превосходящих эти значения отклонений, - неустойчивой, с расходящимися процессами. В этом случае система оказывается устойчивой «в малом» и неустойчивой «в большом». Возможна и обратная картина, когда система устойчива «в большом» и неустойчива «в малом». Если система устойчива при любых отклонениях, то говорят, что система устойчива «в целом».

Рис. П.3.5 Общий вид следящей системы

На рис. П.3.5 изображена следящая система сопровождения с нелинейным чувствительным элементом (дискриминатором). Здесь g ( t ) - задающее воздействие; y ( t ) - управляемая величина; e ( t ) - ошибка сопровождения; F ( е ) - нелинейная зависимость, по которой дискриминатор вырабатывает сигнал управления; W( S ) - передаточная функция линейной части системы; v(t) - внутренний шум.

66

Рис. П.3.6 Статическая характеристика дискриминатора

Типичная статическая характеристика дискриминатора изображена на рис. П.3.6. Сигнал на его выходе отличен от нуля только в пределах аперту-

ры характеристики, т. е. при выполнении условия e e0 . Если это условие

выполняется, то процесс управления может оказаться сходящимся, и следящая система будет осуществлять сопровождение по заданному параметру g ( t ) . При невыполнении этого условия ошибка выходит за пределы апертуры характеристики дискриминатора, пропадает сигнал управления и с большой вероятностью может произойти срыв слежения, т. е. в следящей системе возникает расходящийся процесс без возврата в состояние синхронизации. Это типичный случай устойчивости «в малом» и неустойчивости «в большом».

Ограниченность апертуры характеристики дискриминатора кроме возможного появления срыва слежения определяет и вторую проблему - обеспечение надежного захвата сигнала следящей системой при начальной ее синхронизации. Если рассогласование в системе велико и выходит за пределы апертуры характеристики дискриминатора, то необходимо организовать поисковое движение выходной величины с тем, чтобы при попадании рассогласования в пределы апертуры процессы оказались бы сходящимися и рассогласование в дальнейшем оставалось бы малым.

При этом будет осуществляться слежение за входным сигналом. При узкой апертуре характеристики дискриминатора эта задача может оказаться сравнительно трудной.

В нелинейных системах возможен новый вид установившегося режима, называемый автоколебаниями. Под автоколебаниями понимают устойчивые собственные колебания с постоянной амплитудой и постоянной частотой. Для возникновения автоколебаний не нужен внешний источник возбуждения. Они возникают самопроизвольно и могут существовать неограниченное время.

Общим методом исследования устойчивости нелинейных систем является прямой метод Ляпунова. В его основе лежит теорема Ляпунова об устойчивости нелинейных систем. В качестве аппарата исследования используется так называемая функция Ляпунова, представляющая собой знакоопределенную функцию координат системы, имеющую также знакоопределенную производную по времени. Применение этого метода ограничивается его сложностью.

Более простым методом расчета устойчивости нелинейных систем является метод, разработанный румынским ученым В. М. Поповым. Однако он пригоден для некоторых частных случаев.

Процессы в нелинейной системе могут быть исследованы на основе ку- сочно-линейной аппроксимации. В этом случае нелинейные характеристики отдельных звеньев разбивают на ряд линейных участков, в пределах которых задача оказывается линейной и может быть решена достаточно просто. На границах участков необходимо произвести «сшивание» отдельных кусков

67

процесса в единый процесс. Метод может применяться, если число участков, на которые разбивается нелинейная характеристика, невелико. Это имеет, например, место для релейных характеристик. При большом числе участков метод оказывается слишком громоздким. Однако использование ЭВМ позволяет преодолеть эту трудность и с успехом рассчитывать процессы в нелинейных системах при любых нелинейных характеристиках и вообще при наличии нелинейных зависимостей произвольного вида.

Метод фазовых траекторий в принципе позволяет исследовать системы с нелинейностями произвольного вида, а также с несколькими нелинейностями. При этом в фазовом пространстве строят так называемый фазовый портрет процессов, протекающих в нелинейной системе. По виду фазового портрета можно судить об устойчивости, возможности возникновения автоколебаний, точности в установившемся режиме. Однако размерность фазового пространства равна порядку дифференциального уравнения нелинейной системы. Это затрудняет использование метода для исследования систем, описываемых дифференциальным уравнением выше второго порядка. В случае дифференциального уравнения второго порядка фазовое пространство представляет собой фазовую плоскость, и этот метод может быть с успехом применен.

Дифференциальное уравнение системы автоматического управления может быть преобразовано в систему n дифференциальных уравнений 1-го порядка

с начальными условиями xi (0) . Величины xi (t) можно рассматривать как

координаты некоторой точки М, называемой изображающей точкой, в n- мерном пространстве. Изображающая точка при изменении координат описывает в этом пространстве некоторую кривую, которая называется фазовой траекторией. Совокупность фазовых траекторий, полученных при различных начальных условиях, называется фазовым портретом системы. Наглядное представление фазовых траекторий возможно только для систем, порядок которых не выше второго, или для систем, которые могут быть сведены к системам второго порядка.

Исследование поведения нелинейных систем ниже излагаемым методом возможно только для автономных стационарных систем. Система является автономной, если ее правая часть явно не зависит от времени.

Уравнение автономной системы 2-го порядка можно записать в виде

68

Фазовыми координатами являются выходная переменная системы x1 и скорость ее изменения x2. Разделим второе уравнение системы на первое и получим дифференциальное уравнение фазовых траекторий

Уравнение (П.3.4) однозначно определяет касательную к фазовой траектории во всех точках, кроме тех, в которых одновременно выполняются равенства

В этих точках, которые называются особыми точками, не существует определенного направления касательной к траектории. В особых точках фазовые координаты равны нулю, следовательно, в этих точках система находится в положении равновесия. Для определения особых точек необходимо решить систему (П.3.5). Нужно оценить устойчивость положения равновесия системы в окрестности этих точек.

Таким образом, сутью данного метода является выделение особых точек, построение фазовых траекторий и исследование фазового портрета системы с целью определения областей устойчивости и областей притяжения устойчивых предельных циклов. Статическая характеристика нелинейного звена делит плоскость на участки, где дифференциальные уравнения системы имеют различный вид. Указанная характеристика называется, с этой точки зрения линией переключения.

Типы особых точек фазовых портретов приведены на рисунке П3.7.

69

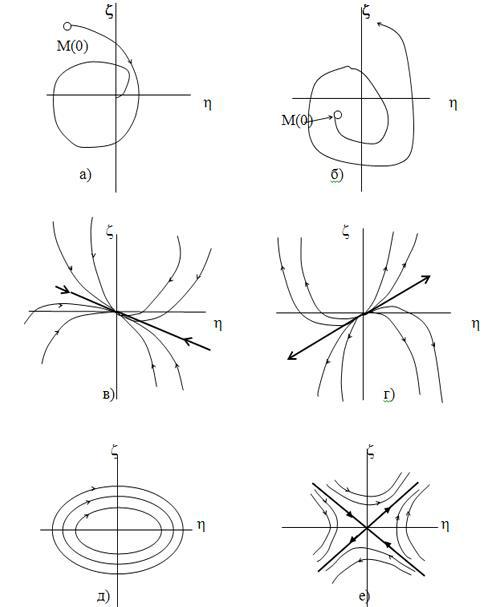
Рис. П.3.7 Типы особых точек фазового портрета

70