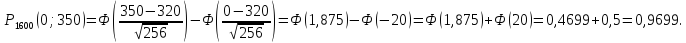Формула Бернулли
Рассмотрим следующий вероятностный эксперимент:
1) последовательно проводится n независимых одинаковых опытов;
2) в каждом из которых имеется лишь два исхода, которые условно назовем «успех» – 1, и «неудача» – 0;
3) во всех опытах вероятность «успеха» – p , и, соответственно, «неудачи» – q = 1− p , неизменны.
Такая последовательность испытаний называется схемой Бернулли, она соответствует весьма многим практическим ситуациям, а именно таким, которые характеризуются «массовостью» явления, что часто встречается в социологии, маркетинге и т.д.
Ясно, что элементарными исходами, в эксперименте по схеме Бернулли, являются всевозможные комбинации вида
100 … 010 - n позиций.
Множество всех таких исходов состоит из 2n элементов.
По теореме умножения вероятностей несложно рассчитать вероятность любого такого исхода, например P (100 ... 010) = p · q · q · ... · q · p · q .
Очевидно,
что любой исход, состоящий из m
«успехов»
и (n–m)
«неудач» имеет вероятность
А
всего таких исходов
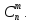Складывая их вероятности, получаем так
называемую формулу
Бернулли
,
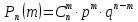которая выражает вероятность того, что при n испытаниях «успех» произойдет ровно m раз.
Задачи:
1) Пусть вероятность того, что телевизор потребует ремонта в течение
гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного
срока из 6 телевизоров: а) не более одного потребует ремонта; б) хотя бы один не
потребует ремонта.
Решение: имеем схему Бернулли с параметрами n = 6 (количество телевизоров), p = 0,2
(вероятность, что телевизор потребует ремонта). Будем использовать формулу Бернулли
(вероятность того, что из n телевизоров ровно k потребуют ремонта):
Cn(k)=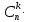
pk(1-p)n-k
а) Вероятность того, что не более одного потребует ремонта:
P 6(k ≤ 1) = P6 (1) + P6 (0) = C61 ·0,21·0,85 +C60 ·0,20 ·0,86 = 6·0,2·0,85 + 0,86 ≈ 0,655.
б) Вероятность, что хотя бы один телевизор не потребует ремонта (противоположное
событие – все потребуют ремонта):
1- P6(6) =1-C66·0,26·0,80 =1- 0,26 ≈ 0,9999.
2) Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными.
Решение: здесь опыт заключается в проверке каждой из 30 деталей на качество. Событие А - «появление нестандартной детали», его вероятность p = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли находим
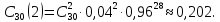
Приближенная формула Пуассона
При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет k раз, используют формулу Пуассона:
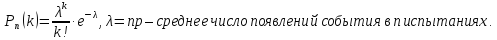
Эта
формула дает удовлетворительное
приближение для
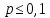и
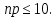
Задачи:
1) С базы в магазин отправлено 4000 тщательно упакованных доброкачественных
изделий. Вероятность того, что изделие повредится в пути, равна 0.0005. Найти
вероятность того, что из 4000 изделий в магазин прибудут 3 испорченных изделия.
Решение: имеем схему Бернулли с параметрами n = 4000 , p = 0,0005. Так как n = 4000
велико, а p = 0,0005 мало, можно использовать для вычислений приближенную формулу
Пуассона:
Pn(k)=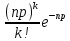
-
вероятность того, что из n
изделий
окажется ровно k
поврежденных
в
пути.
Так как np
=
4000×0,0005 = 2 , получаем формулу
.
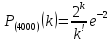Вероятность того, что из 4000 изделий в магазин прибудут 3 испорченных изделия:
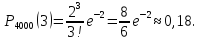
2) Вероятность выпуска бракованного сверла (повышенной хрупкости) равна 0,02. Свёрла укладывают в коробки по 100 штук. Определить вероятность того, что число бракованных свёрл в коробке не превосходит трёх.
Решение: имеется схема Бернулли: n = 100, p = 0,02; q = 0,98. Вероятность наступления события мала, количество производимых испытаний велико (np < 9). Используем приближённую формулу Пуассона
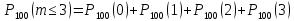
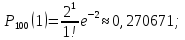
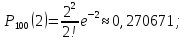
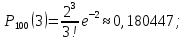
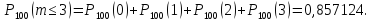
Формулы Лапласа
Пусть
в каждом из n
независимых испытаний событие A
может произойти с вероятностью p,
q=1-p.
Обозначим через
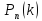- вероятность ровно k
появлений события A
в n
испытаниях. Кроме того, пусть
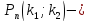вероятность того, что число появлений
события А находится между
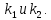
Локальная теорема Лапласа:
Если n – велико, а р – отлично от 0 и 1, то
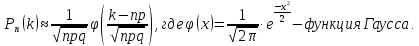
Интегральная теорема Лапласа:
Если n – велико, а р – отлично от 0 и 1, то
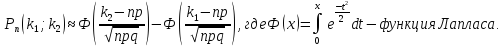
Функции Гаусса и Лапласа обладают свойствами, которые необходимо знать при использовании таблиц значений этих функций:
1.
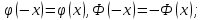
2.
при больших
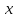верно
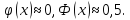
Задачи:
1) В продукции некоторого производства брак составляет 15%. Изделия отправляются потребителям (без проверки) в коробках по 100 штук. Найти вероятности событий: В – наудачу взятая коробка содержит 13 бракованных изделий; С – число бракованных изделий в коробке не превосходит 20.
Решение:
изготовление
детали – это испытание, в котором может
появиться событие А – изделие бракованное
– с вероятностью р=0,15. Находим n·p=15,
n·p·q=12,75.
Можно применить формулы Лапласа: P(B)
=
)=0,28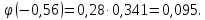
P(C)
=
Приблизительно 9,5% всех коробок содержат 13 бракованных изделий и в 92% коробок число бракованных не превосходит 20.
2) Магазин получил 1000 бутылок молока. Вероятность того, что при перевозке бутылка разобьется, равна 0,003. Найти вероятность того, что магазин получит ровно две разбитых бутылки.
Решение: по схеме Бернулли имеем: n = 1000, p = 0,003, q = 0,997. Отсюда n · p · q = 2,991. Поскольку число n = 1000 достаточно велико, подставляем все числа в формулу локальной теоремы Лапласа:
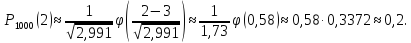
3) Страхуется 1600 автомобилей. Вероятность того, что автомобиль попадет в аварию равна 0,2. Сосчитать вероятность того, что количество аварий не превысит 350.
Решение: имеем n = 1600, p = 0,2. Сосчитаем q = 1-p = 0,8. np = 320, npq = 256.
Применим интегральную формулу Лапласа:
