31 Равномерная непрерывность функций

Определение равномерной непрерывности

Функция f: X → R называется равномерно-непрерывной на множестве X, если

Если функция f не является равномерно-непрерывной, то это означает следующее:

Теорема Кантора

Если функция f: [a, b] → R непрерывна на сегменте [a, b], то она равномерно непрерывна на этом сегменте.

Доказательство.

Доказательство этой теоремы проведем методом от противного.

Надо доказать:

Противоположное утверждение:

1. Построение последовательностей.

Возьмем любую последовательность _n, которая монотонно убывает до нуля, т.е.

₁>₂>₃>…_n0, n

Тогда для каждого _n

Перебирая все _n мы получим две последовательности {x_n} и .

2. Выделение сходящихся подпоследовательностей.

Рассмотрим последовательность {x_n}. Она ограничена, т.к. a x_n b. По лемме Больцано-Вейерштрасса, из нее можно выделить сходящуюся подпоследовательность , т.е. . Заметим, что c[a,b] в силу замкнутости [a,b]. А что можно сказать о подпоследовательности ? Т.к. , то

.

Но так как  а  то по теореме “о двух милиционерах” отсюда следует, что также , т.е. подпоследовательность сходится к тому же пределу c, что и .

3. Сведение к противоречию.

Рассмотрим теперь последний квантор

Переходя к пределу k и учитывая непрерывность функции y=|x|, получим:

 

В силу непрерывности f(x) , так что получаем, что

|f(c)-f(c)| 

т.е. получаем, что 0. Это противоречит квантору , где строго больше 0.

32 Определение производной

   Пусть на некотором промежутке Х определена функция y = f (x). Возьмём любую точку х₀  Х и зададим аргументу х в точке х₀ произвольное приращение Δ xтакое, что точка х₀ + Δ x также принадлежит Х. Функция получит приращение Δy = f (x₀ + Δ x) − f (x₀).    Производной функции у = f (x) в точке х₀ называется предел отношения приращения функции в этой точке к приращению аргумента при Δ x → 0 (при условии, что этот предел существует)

.

   Правой производной функции у = f (x) в точке х ₀ называется предел отношения приращения функции в этой точке к приращению аргумента при Δ x → + 0 (при условии, что этот предел существует)

.

   Левой производной функции у = f (x) в точке х₀ называется предел отношения приращения функции в этой точке к приращению аргумента при Δ x → − 0 (при условии, что этот предел существует)

.

   Если левая производная функции у = f (x) в точке х₀ совпадает с правой производной функции у = f (x) в этой точке, то эти односторонние производные совпадают с самой производной функции в данной точке. Если для некоторого значения х₀ выполняется условие

 (или ),

то говорят, что в точке х₀ функция имеет бесконечную производную знака плюс (или знака минус).

Геометрический смысл производной

   Пусть функция y = f (x) определена на интервале (a, b) и пусть точка М₀ на графике функции соответствует значению аргумента х₀, а точка M – значению х₀ + Δx. Проведем через точки М₀ и M прямую и назовем ее секущей. Обозначим через φ(Δx) угол между секущей и осью Ох. Если существует предел

,

то прямую с угловым коэффициентом k = tg φ₀, проходящую через точку М₀ (х₀, f(x₀)), называют предельным положением секущей М₀M при Δx → 0.    Определение. Касательной τ к графику функции y = f(x) в точке М₀ будем называть предельное положение секущей М₀M при Δx → 0.    Из определения следует, что для существования касательной достаточно, чтобы существовал предел

,

причем значение предела φ₀ равно углу наклона касательной к оси Ох. Если функция y = f(x) имеет в точке х₀ производную, то существует касательная к графику функции y = f(x) в точке М₀(х₀, f(x₀), причем угловой коэффициент этой касательной (т.е. тангенс угла наклона ее к оси Ох) равен производной f ' (x₀). Нажми на линк для просмотра рисунка   Действительно, из треугольника M₀MP получаем, что тангенс угла наклона хорды равен

.

Из определения производной функции в точке при Δx → 0 следует

.

Из непрерывности функции tg α следует

,

cледовательно, существует предел и левой части равенства. Таким образом, получаем

.

Это означает, что существует касательная к графику функции y = f(x) в точке М₀(х₀, f(x₀)), причем угол наклона φ₀ этой касательной к оси Ох равен arctg f '(x₀) и, значит, угловой коэффициент касательной равен

tg φ₀ = f ' (x₀),

что и требовалось доказать.    Итак, производная функции y = f(x) в точке х₀ равна угловому коэффициенту касательной к графику функции y = f(x) в точке М₀(х₀, f(x₀)). Воспользовавшись уравнением пучка прямых, получим уравнение касательной, проведённой к графику функции в данной точке

y - y₀ = f ' (x₀)·( x - x₀ ).

Геометрически дифференцируемость функции в точке означает наличие определённой касательной в точке.  Прямая, перпендикулярная касательной, проведённой к графику функции в данной точке, называется нормалью, проведённой к графику функции в данной точке (Нажми на линк для просмотра рисунка). Используя условие перпендикулярности прямых с угловым коэффициентом и уравнение пучка прямых, получим уравнение нормали в виде

.

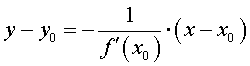 Длина Т отрезка АМ₀ касательной называется д л и н о й касательной. Проекция этого ортезка на ось ОХ, т.е. отрезок АС казывается п о д к а с а т е л ь н о й. Длина N отрезка ВМ₀ называется длиной нормали. Проекция отрезка ВМ₀ на ось ОХ называется поднормалью.