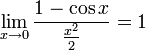20 Первый замечательный предел

Доказательство

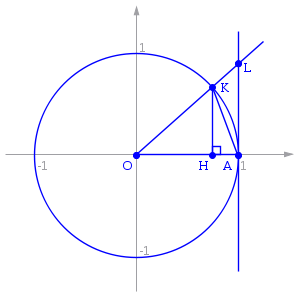
Рассмотрим односторонние пределы  и  и докажем, что они равны 1.

Пусть . Отложим этот угол на единичной окружности (R = 1).

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.

Очевидно, что:  (1)(где S_sectOKA — площадь сектора OKA)

(из : | LA | = tgx)

Подставляя в (1), получим:

Так как при :

Умножаем на sinx:

Перейдём к пределу:

Найдём левый односторонний предел:

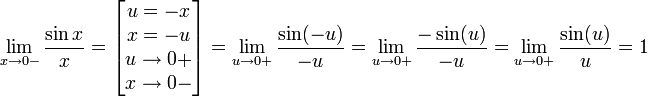
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия

• 

• 

• 

• 

21 Второй замечательный предел

 или 

Доказательство второго замечательного предела:

Доказательство для натуральных значений x  [показать]

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что . Рассмотрим два случая:

1. Пусть . Каждое значение x заключено между двумя положительными целыми числами: , где — это целая часть x.

Отсюда следует: , поэтому

.

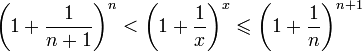Если , то . Поэтому, согласно пределу , имеем:

.

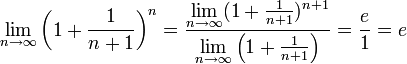
По признаку (о пределе промежуточной функции) существования пределов .

2. Пусть . Сделаем подстановку − x = t, тогда

.

Из двух этих случаев вытекает, что  для вещественного x.    

Следствия

1. 

2. 

3. 

4. 

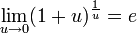
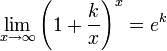
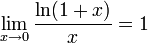
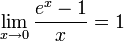
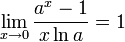5.  для , 

6. 

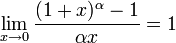
23 Сравнение функций.

Определение 15 (символ О). Если для функций f(x), g(x) существуют постоянные c>0, >0, такие, что |f(x)| c |g(x)| при |x-a|<, x a, то говорят, что f является ограниченной по сравнению с функцией g в окрестности точки a и пишут, что f(x) = O(g(x)) при x a.

Данное определение переносится и на случай, когда x, x.

Пример 12.

1. Так как |1/x²|  |1/x| при |x|  1, то 1/x² = O(1/x) при x ;

2. 1/x = O(1/x²) при x 0 так как |1/x| 1/x² при |x| 1.

Запись f=O(1) при x a означает, что функция f(x) ограничена в некоторой окрестности точки a.

Определение 16 (функции одного порядка). Если f=O(g) и g=O(f) при x a  f и g — одного порядка при x a.

Пример 13. Функции f(x) = x(2+sin 1/x) g(x) = x x  0 являются бесконечно малыми одного порядка при x a , так как

f/g = (x(2+sin 1/x))/x = 2+sin 1/x = |2+sin 1/x|  3  f=O(g), g/f = 1/|2+sin 1/x|  1 g=O(f).

Определение 17 (эквивалентные функции). Функции f(x) и g(x) называются эквивалентными при x a, если (x): f(x) =  (x)g(x), где lim_x a (x) = 1.

Иначе говоря функции эквивалентны при x a, если предел их отношения при xa равен единице. Справедливы следующие соотношения, их еще называют асимптотическими равенствами:

sin x ~ x, x 0

(1)

tg x ~ x, x  0, arcsin x ~ x, x  0, arctg x~ x, x  0

e^x-1~ x, x 0

ln (1+x)~ x, x0

(2)

m-1~ mx, x0

(3)

Следующая теорема удобна для применения на практике при вычислении пределов.

Теорема 7. Пусть f(x)~ f1(x), g(x)~ g1(x) при x a Тогда если существует предел

lim_x af1(x)/g1(x),

то существует

lim_x af(x)/g(x),

причем

lim_x af1(x)/g1(x) = lim_x af(x)/g(x).

Пример 14. Найти предел

lim_x 0(ln cos x)/sin x2

Решение. Для решения воспользуемся асимптотическими равенствами (1), (2)

lim_x 0(ln cos x)/sin x2 = lim_x 0 (ln(1-2sin²x/2))/x2 =

= lim_x 0(-2sin²x/2)/x2 = -2lim_x 0(x2/4)/x2 = -1/2.

Определение 18 (символ о). Говорят, что функция f является бесконечно малой по сравнению с g при x a, и пишут f=o(g), x a, если выполнено соотношение f(x) = (x)g(x), где lim_x a (x) = 0. Иначе говоря lim_x a f(x)/g(x) = lim_x a (x) = 0.

Пример 15.

1. x2 = o(x) при x  0, так как lim_x  0x2/x = lim_x  0x = 0;

2. 1/x2 = o(1/x) при x  так как lim_x x/x2 = lim_x 1/x = 0

Справедлива теорема.

Теорема 8. Для того, чтобы функции f(x), g(x) были эквивалентными при xa необходимо и достаточно, чтобы при x a выполнялось хотя бы одно из условий

f(x) = g(x)+o(g(x))

или

g(x) = f(x)+o(f(x)).

Заметим, что функции g(x) в первом условии и соответственно функция f(x) во втором называются главной частью функции f(x) (g(x)).

Пример 16.

1. Функция x – главная часть функции sin x при x 0, так как sin x = x+o(x) при x 0;

2. Если P_n(x) = a_nxⁿ+...+a₁x+a₀, a_n 0, то функция a_nxⁿ является главной частью P_n(x) при x, так как P_n(x) = a_nxⁿ+o(xⁿ) при x.

Метод выделения главной части бесконечно малых применяется к вычислению пределов.

Пример 17. Найти предел

Решение. Используя асимптотическое равенство (3) и асимптотическое равенство (1), а также учитывая, что x2 = o(x) при x 0 (см. пример 15) и f=o(x2) является функцией o(x) при x 0, найдем

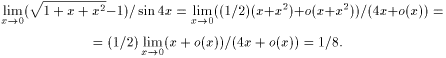
Определение 19. Если f=o(g) при x a и g(x) - бесконечно малая при x a, то говорят, что f(x) - бесконечно малая более высокого по сравнению с g(x) порядка при x a.

Пример 18. x²- бесконечно малая более высокого порядка по сравнению с x при x 0

Определение 20. Если f(x), g(x) -бесконечно большие при x a и f=o(g) при x a, то говорят, что g - бесконечно большая более высокого порядка по сравнению с f .

Пример 19. Функции f=x3+x2+2x+1, g=x4+3x2 -бесконечно большие при x, и так как lim_x f/g=0, то g — бесконечно большая более высокого порядка по сравнению с f

Отметим некоторые правила обращения с символами o(), O().

Предложение 2.

1. o(f)+o(f) = o(f)

2. o(f) тем более есть O(f)

3. O(f)+O(f) = O(f)

4. Если g 0, то o(f)/g=o(f/g), O(f)/g=O(f/g).