Вывод уравнения Кельвина

Искривление поверхности жидкости приводит к изменению её потенциала на (?) величину ΔМж

ΔМж = Мж – Мж = 2σ ж – г * Vм/r (1) ΔМж = 2σ ж – г * Vм/r (1)

Для того, чтобы в системе сохранилось сост-е равновесия химич.потенциал пара также должен измениться на величину ΔМп

При изменении ΔМп = ΔМж (2)

ΔМп = Мп-Мп (3); Мп=Мт+RTlnPr (4) – давление насыщенного пара над искривлённой поверхностью

Мп = Мт + RTlnP0 (5) – давление насыщенного пара над плоской поверхностью

(4) и (5) подставим в (3)

ΔМп = Мт + RTlnPr – Мт – RTlnP0 = RT (lnPr – lnP0) = RTln Pr/P0

Таким образом ΔМпара = RTln Pr/P0 (6)

В (2) подставляем формулы (1) и (6)

2σ ж – г * Vм/r= RTln Pr/P0 (7) – относительное давление пара, находящегося в равновесии с мениском жидкости у кот.радиус кривизны r.

Из (7) выразим величину относительного давления пара

=2σ ж – г * Vм/r (RT) (8) – уравнение Кельвина

=2σ ж – г * Vм/r (RT) (9)

Если поверхность имеет неправильную форму, то уравнение Кельвина записывается в виде:

=2σ ж – г * Vм/r (RT) (1/г1+1/г2) (10)

Г1, г2 – главные радиусы кривизны поверхности, следовательно, при положительной кривизне Pr/P0>0, т.е.над каплей жидкости давление пара выше, чем над ровной поверхностью и тем выше, чем < радиус кривизны поверхности.

При отрицательной кривизне Pr/P0<0 и конденсация пара над искривлённой поверхностью в капилляре будет происходить при меньшем давлении, чем над ровной поверхностью.

Правило Гиббса-Кюри –

Устанавливает условия равновесной формы тела. Равновесной формой тела считается та, кот.соответствует минимуму поверхностной энергии Гиббса при V=const

ΔG= =min, (1)

где удельная свободная поверхностная энергии i-той части тела

Si – площадь i-той части тела

Правила Гиббса-Кюри для жидкости

Жидк.тела изотопные, т.е.св-ва жидкости в любой т.тела одинаковые, и, следовательно, =const

Тогда (1) принимает вид: ΔG= =min (2)

Условием равновесной формы жидк.тел является минимум площади поверхности вследствие чего жидкость принимает сферическую форму.

Принцип равновесной формы тела для кристалл (закон Бульора)

Тв.тела анизотропны, т.е.их св-ва в различ.т.тела не одинаковы. В этом случае минимуму энергии Гиббса равновесного кристалла отвечает условие пропорциональности свободной поверхностной энергии границ кристаллов, их расстоянием от центра кристалла.

… =const

Зависимость т/д-ной реакционной способности от дисперсности. Реакционная способность в-ва определяется энергией Гиббса, которая характеризует способность в-ва перейти из 1-ой фазы в др., вступить в хим.реакцию и определить удалённость длинного состояния системы от равновесного.

Для установления зависимости т/д используют объединения уравнение 1-го и 2-го з.термодинамики.

dGр=-S*dT+V*dp (1)

Для индивидуального в-ва V=Vм, и если система находится при Т=const, то (1) принимает вид:

dGd = Vм*dp или ΔG= Vм*Δp (2)

В (2) вместо Δр представляем его выражение из уравнения Лапласа

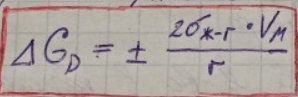(3)

Уравнение (3) выражает зависимость т/д-ской реакцион.способности от дисперсности

D=1/2r

Чем выше дисперсность (т.е.<размер частиц), тем > энергия Гиббса и выше т/д-сная реакционная способность вещества.

Т/д-скую реакционная способность от дисперсности можно выразить для веществ через р-римость

где Ср – р-римость веществ в дисперсном состоянии

Cs – р-римость недисперсированного вещества

Зная это уравнение, можно вычислить размер частиц твёрдых веществ.

Влияние дисперсности на температуру фазового перехода

Уравнение (1) при V=const принимает вид:

(5)

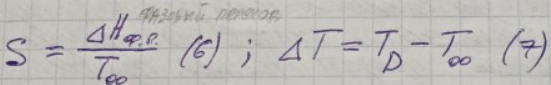
В (9) подставим ΔG из влияния дисперсности на т/д-скую реакционную способность.

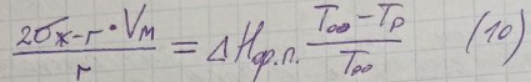
Из (10) выразим изменение температуры фазового перехода, обусловленного дисперсностью

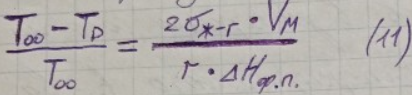
Из (11) видно, что с увеличением дисперсности в-ва температура фазового перехода уменьшается.

Вывод:

В производственных условиях с увеличением дисперсности происходит увеличением площади реакционной поверхности, что благоприятно сказывается на производительности, позволяет снизить температуру процесса и удельный расход энергии. Существует оптимальное значение дисперсности порошков, при кот.взаим-е происходит наиболее интенсивно. С целью определения оптимальной дисперсности и определяют удельную поверхность порошков.