
Коллоидные частицы золота имеют дисперсность равную D=108 м-1. Какой длины (L) будет нить, если 1 кг частиц золота, имеющих кубическую форму расположить друг за другом. Плотность золота частиц фазы 19,6 · 103 кг/м3.


Определите величину удельной поверхности суспензии каолина плотностью 2,5 · 103 кг/м3. Частицы дисперсной фазы имеют сферическую форму со средним диаметром равным 0,5 · 10-6 м. Суспензию считать монодисперсной. Величину удельной поверхности дать в следующих единицах измерения: (м-1, м2/кг)
ИЛИ
Определите величину удельной поверхности суспензии каолина плотностью 2,5 · 103 кг/м3, состоящей из шарообразных частиц со средним диаметром 0,5 · 10–6 м. Суспензию считайте монодисперсной. Ответ дайте в м–1 и в м2/кг.



Определите численную концентрацию гидрозоля Al2O3 исходя из следующих данных: массовая концентрация 0,3 г/л, коэффициент диффузии сферических частиц золя 2∙10-6 м2/сут, плотность Al2O3 4 г/см3, вязкость среды 1 ∙ 10-3 Па ∙ c, температура 293 К.

Определить частичную концентрацию гидрозоля Al2O3, если его массовая концентрация 0,3 г/л, коэффициент диффузии сферических частиц золя 2∙10-6 м2/сут, плотность гидрозоля 4 г/см3, вязкость дисперсионной среды 10-3 Н·с/м2 и температура 293 К.

Задача №2.1
Используя зависимость
поверхностного натяжения жидкости от
температуры (таблица), определите
внутреннюю энергию и энтропию
поверхностного слоя, теплоту образования
единицы поверхности и критическую
температуру. Какие выводы следуют из
линейного характера зависимости
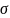 = f(T) и отрицательного знака температурного
коэффициента поверхностного натяжения?
Вещество – n-ксилол
= f(T) и отрицательного знака температурного
коэффициента поверхностного натяжения?
Вещество – n-ксилол
V |
*10-3 |
t, ⁰C |
T, K |
|
12 |
- |
- |
- |
- |
28,31 |
20 |
293 |
0,7022 |
|
27,22 |
30 |
303 |
0,6942 |
|
26,13 |
40 |
313 |
0,6860 |
|
25,06 |
50 |
323 |
0,6778 |
|
24,02 |
60 |
333 |
0,6694 |
Внутренняя полная поверхностная энергия
вычисляется по уравнению
 .
На основании объединённого уравнения
1-го и 2-го законов термодинамики можно
записать
.
На основании объединённого уравнения
1-го и 2-го законов термодинамики можно
записать
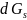 =
=
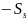 *dT
(2). Из (2) выразим
*dT
(2). Из (2) выразим
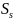 = -
= -
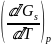 =
=
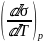 (3)
(3)
=
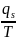 (4). В выражение (4) подставим (3):
=
(4). В выражение (4) подставим (3):
=
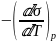 (5)
(5)
Следовательно,
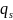 = -T
(6)
= -T
(6)
Величину
из (6) подставляем в уравнение (1):
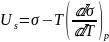 (7). Уравнение (7) – это уравнение
Гиббса-Гельмгольца, выражающее зависимость
всех термодинамических свойств
поверхностного слоя от температуры.
– температурный коэффициент поверхностного
натяжения. Он характеризует величину,
на которую изменяется поверхностное
натяжение с увеличением температуры
(иногда обозначается
(7). Уравнение (7) – это уравнение
Гиббса-Гельмгольца, выражающее зависимость
всех термодинамических свойств
поверхностного слоя от температуры.
– температурный коэффициент поверхностного
натяжения. Он характеризует величину,
на которую изменяется поверхностное
натяжение с увеличением температуры
(иногда обозначается
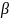 )
)
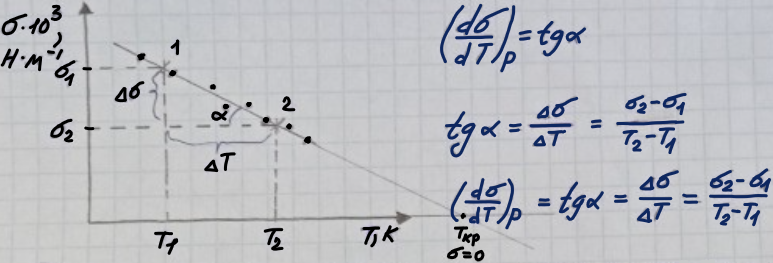
Эту величину находят графически путём построения графика зависимости на = f(T)
Температурный коэффициент поверхностного натяжения имеет знак «-». Это свидетельствует о том, что с увеличением температуры величина поверхностного натяжения уменьшается. Уменьшение поверхностного натяжения с ростом температуры обусловлено тем, что тепловое движение молекул возрастает, между ними увеличивается расстояние и ослабляется межмолекулярное взаимодействие (для индивидуальных жидкостей).
Для растворов уменьшение поверхностного натяжения с ростом температуры объясняется возрастанием взаимной растворимости компонентов фаз.
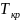 – такая температура, при которой исчезает
различие между фазами, система становится
гомогенной и все термодинамические
параметры стремятся к 0.
– такая температура, при которой исчезает
различие между фазами, система становится
гомогенной и все термодинамические
параметры стремятся к 0.
Критическую температуру более точно вычисляют по уравнению Этвеша:
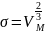 = К(
-Т),
где
= К(
-Т),
где
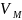 – мольный объём
– мольный объём
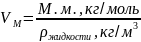 , [м3/моль]
, [м3/моль]
К – коэффициент пропорциональности, который в системе СИ равен для неполярных веществ К=2,1*10-7, для полярных веществ: К < 2,1*10-7. Для веществ с большой молярной массой K > 2,1*10-7
Зависимость индивидуальных жидкостей
от поверхностного натяжения выражается
уравнением:
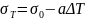 ,
где a – величина, обратная
по знаку температурного коэффициента
поверхностного натяжения,
,
где a – величина, обратная
по знаку температурного коэффициента
поверхностного натяжения,
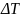 =Тзад-Тст.
=Тзад-Тст.
Т.к.
=
=
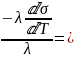 -
;
-
;
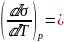 Н/м*к
Н/м*к
Решение
Для нахождения температурного коэффициента строим график зависимости = f(T)
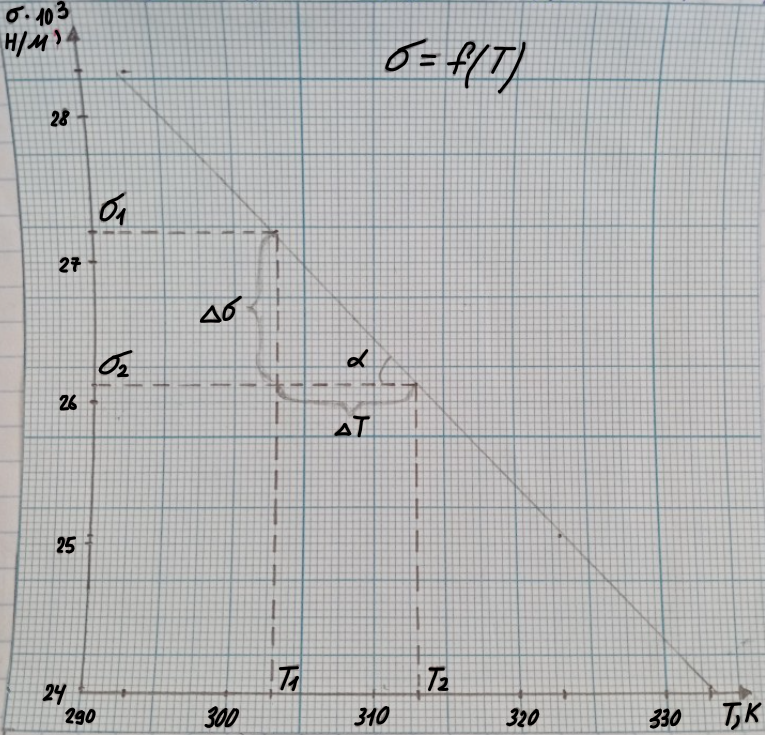
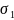 = 27,22*103 Н/м;
= 27,22*103 Н/м;
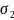 = 26,13*103 Н/м
= 26,13*103 Н/м
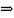
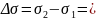 -1,09*103 Н/м
-1,09*103 Н/м
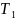 = 303 К;
= 303 К;
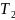 = 313 К
= 313 К
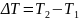 = 10 К
= 10 К
tg α =
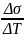 =
=
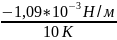 = 0,109*10-3
= 0,109*10-3
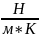 =
=
Т. к. энтропия поверхностного слоя = - , то = -0,109*10-3 .
Теплота образования единицы поверхности
определяется по формуле
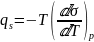 :
:
1) = -273*(-0,109*10-3) = 29,76*10-3 Н/м
2) = -283*(-0,109*10-3) = 30,85*10-3 Н/м
3) = -293*(-0,109*10-3) = 31,94*10-3 Н/м
4) = -303*(-0,109*10-3) = 33,03*10-3 Н/м
5) = -313*(-0,109*10-3) = 34,18*10-3 Н/м
6) = -323*(-0,109*10-3) = 35,21*10-3 Н/м
7) = -333*(-0,109*10-3) = 36,30*10-3 Н/м
Строим график зависимости = f(T).
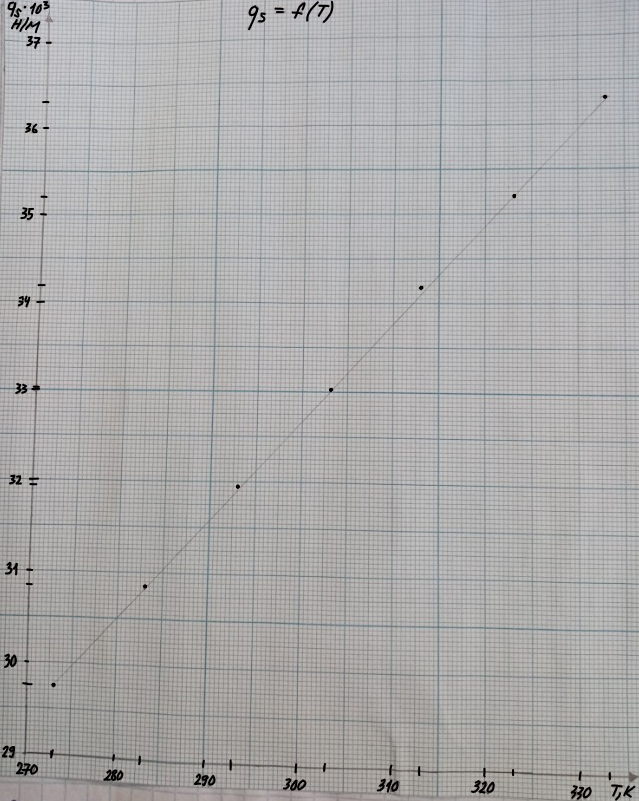
Энтропия поверхностного слоя = . При вычислении будет постоянным и равным 1,09*102 .
Т. о., график зависимости = f (T) будет иметь вид:
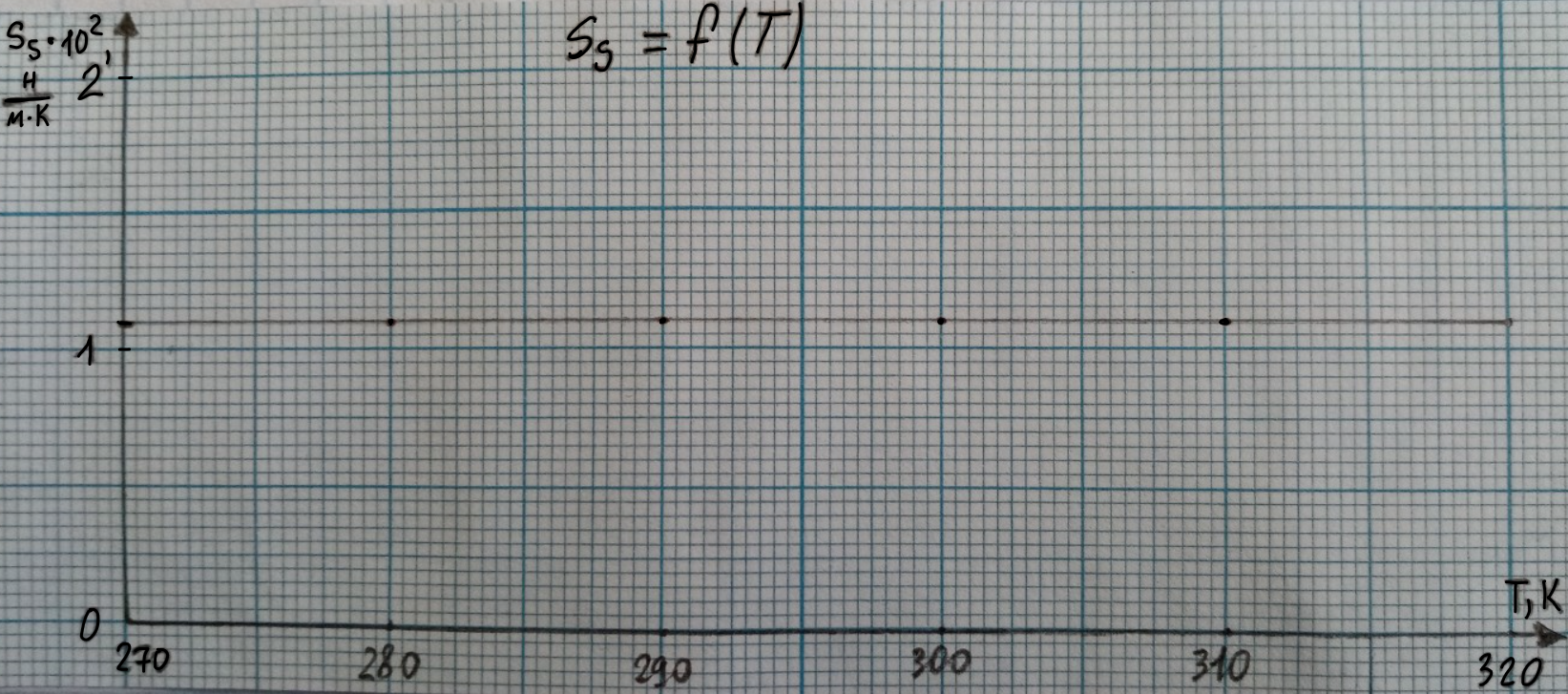
Внутренняя полная поверхностная энергия Us может быть найдена по формулам:
Us
=
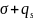 или Us
=
или Us
=
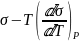 .
Я воспользуюсь формулой Us
=
.
Я воспользуюсь формулой Us
=
1) -
2) -
3) Us
= 28,31*10-3+31,94*10-3 = 60,25*10-3
Н/м
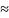 60*10-3 Н/м
60*10-3 Н/м
4) Us = 27,22*10-3+33,03*10-3 = 60,25*10-3 Н/м 60*10-3 Н/м
5) Us = 26,13*10-3+34,18*10-3 = 60,31*10-3 Н/м 60*10-3 Н/м
6) Us = 25,06*10-3+35,21*10-3 = 60,27*10-3 Н/м 60*10-3 Н/м
7) Us = 24,02*10-3+36,30*10-3 = 60,32*10-3 Н/м 60*10-3 Н/м
Строим график зависимости Us = f (T)
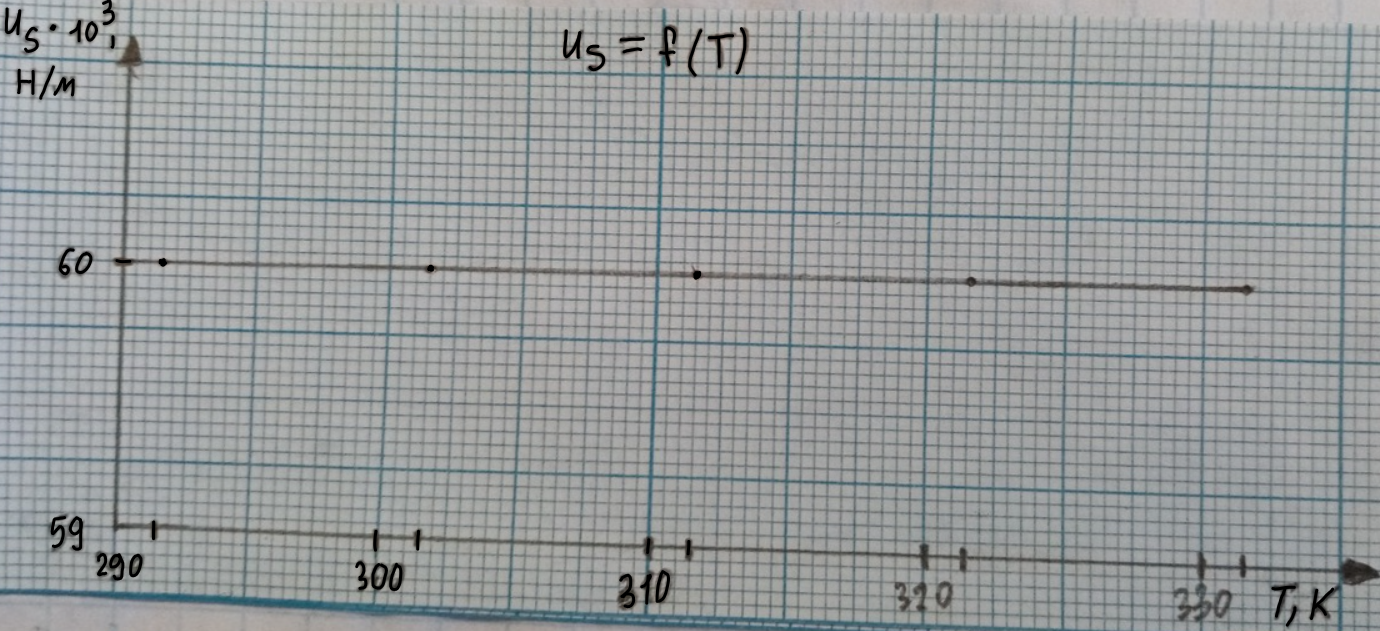
Критическую температуру более точно
вычисляют по уравнению Этвеша:
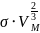 = К(
-Т)
= К(
-Т)
– Т =
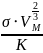
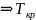 =
+Т
=
+Т
К = 2,1*10-7, М (n-ксилол)
= 106*10-3 кг/моль,
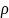 (n-ксилол)
= 861,1 кг/м3
(n-ксилол)
= 861,1 кг/м3
Тогда
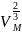 =
=
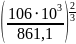 24,7*10-4 м3/моль
24,7*10-4 м3/моль
Т. о., критическая температура (при
поверхностном натяжении
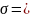 28,31
и температуре 20⁰С) равна
28,31
и температуре 20⁰С) равна
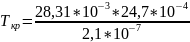 +293
626 К
+293
626 К
Справочное значение = 632 К, т.е. полученная мною = 626 К является верной.
Вывод: с помощью зависимости поверхностного натяжения жидкости от температуры (табл.) определил внутреннюю энергию Us, энтропию поверхностного слоя Ss, теплоту образования единицы поверхности и критическую температуру по уравнению Этвеша (для большей точности).
Вычислить коэффициент растекания и определить, будет ли растекаться н-гексан по поверхности воды, если работа когезии для н-гексана равна 36,8 мДж/м2, а работа адгезии гексана к воде равна 40,1 мДж/м2.
Решение:
Для ответа на вопрос необходимо определить
коэффициент растекания: f
=
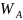 -
-
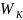 = 40,1 - 36,8 = 3,3 мДж/м2.
= 40,1 - 36,8 = 3,3 мДж/м2.
Вывод: f > 0, растекание происходит.
Верхний водный слой раствора
сахарозы (G1)
имеет поверхностное натяжение
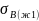 = 61,0 мДж/м2,
бензольный слой (G2)
имеет поверхностное натяжение
= 61,0 мДж/м2,
бензольный слой (G2)
имеет поверхностное натяжение
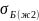 = 26, 9 мДж/м2.
Соответствует ли это правилу Антонова,
если межфазное поверхностное натяжение
= 26, 9 мДж/м2.
Соответствует ли это правилу Антонова,
если межфазное поверхностное натяжение
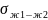 = 34,1 мДж/м2.
= 34,1 мДж/м2.
Решение:
=
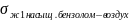 –
–
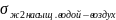 = 34,1. Правилу Антонова подчиняется.
= 34,1. Правилу Антонова подчиняется.
Краевой угол для воды на коже человека при 20⁰С Ө=75⁰, а на полиэтилене Өп = 103⁰. На сколько больше работа адгезии в 1-ом случае по сравнению со 2-ым, если при заданной температуре H2O = 72,75 мДж/м2?
Решение:
Вычислим работу адгезии для заданных углов по уравнению Юнга-Дюпре:
=
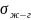 (1 + cosӨ)
(1 + cosӨ)
1)
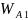 =
=
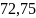 (1 + cos 75) = 139,8 мДж/м2
(1 + cos 75) = 139,8 мДж/м2
2)
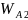 =
(1 + cos 103) = 15,84 мДж/м2
=
(1 + cos 103) = 15,84 мДж/м2
> , т. к. поверхность кожи человека гидрофильная, а полиэтилена – гидрофобная.
Найдите термическую характеристику смачивания ( ) используя данные, приведённые в таблице:
(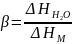 , где
, где
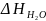 – теплота, выделенная при смачивании
тв. тела Н2О, а
– теплота, выделенная при смачивании
тв. тела Н2О, а
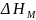 – неполярной жидкостью).
– неполярной жидкостью).
Твёрдое вещество |
Жидкость |
Теплота смачивания, кДж/кг |
Поверхность твёрдого вещества |
Уголь |
Вода Гексан |
24,72 67,0 |
= 0,37, т.е. <1 Гидрофобная (олеофильная) |
SiO2 |
Вода Гексан |
38,11 18,42 |
= 2, т.е. <1 Гидрофильная (олеофобная) |
Графит |
Вода Бензол |
6,29 6,71 |
= 0,94, т.е. <1 Гидрофобная (олеофильная) |

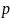 * 10-3,
кг/м3
* 10-3,
кг/м3