- •Задача №3
- •Таким образом, величина « » может рассматриваться не только как удельная свободная поверхностная энергия, но и как сила, отнесённая к единице длины контура, ограничивающего поверхность.
- •Задача №2.1
- •Решение
- •Практика №4
- •Кагезия.
- •Смачивание
- •Анализ уравнения Юнга
- •Значение смачивания
- •Решение задач
- •Задание №2.2. Адсорбционные равновесия. Вариант 3
- •Практика №5.
- •Практика №6. «Капиллярные явления»
Практика №2
«Молекулярно-кинетические свойства дисперсных систем»
К этим свойствам относятся броуновское движение, диффузия, осмос, диффузионно-седиментационное равновесие (гипсометрический закон Палласа-Перрена) и седиментация, кривизна поверхности.
Все эти свойства дисперсных систем типичны аналогичным свойствам истинных растворов, но проявляются в сотни и тысячи раз слабее ввиду больших различий в размерах частиц.
Задача №1
Коллоидные частицы золота имеют дисперсность равную D=10^8 м^-1. Какой длины (L) будет нить, если 1 кг частиц золота, имеющих кубическую форму расположить друг за другом. Плотность золота частиц фазы 19,6*10^3 кг/м3

Задача №2
Определите величину удельной поверхности суспензии каолина плотностью 2,5 · 10^3 кг/м3. Частицы дисперсной фазы имеют сферическую форму со средним диаметром равным 0,5*10^-6 м. Суспензию считать монодисперсной. Величину удельной поверхности дать в следующих единицах измерения: (м^-1, м^2/кг)
Дано: р=2,5 · 10^3 кг/м3 d=0,5*10^-6 м |
Решение: |
Молекулярные кинетические свойства наблюдаются только в свободных дисперсных системах. Суспензия каолина – дисперсная система типа т/ж, где т – дисперсная фаза, в качестве которой выступают раздробленные частицы каолина, а дисперсн. среда-вода |
|
Найти: Sуд. (м^-1, м^2/кг) - ? |
Так как дисперсная система монодисперсна
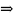 все
частицы дисперсной фазы имеют одинаковые
размеры.
все
частицы дисперсной фазы имеют одинаковые
размеры.
Sуд = Sсум/Vсум или Sуд = Sсум/Мсум
Удельная поверхность характеризует поверхность, приходящуюся на 1 м2 (или см2) вещества поверхностной фазы.
1. При расчёте удельной поверхности по фазе (1):
а) если частица имеет сферическую форму
Sуд =
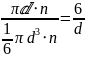
б) частица имеет кубическую форму
Sуд=
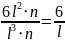
Графически зависимость удельной поверхности от размера частиц имеет вид:
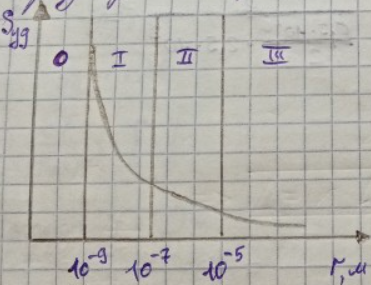
Обл.I относится к высокодисперсным системам
Обл.II относится к микрогетерогенным системам
Обл.III относится к грубодисперсным системам
Нулевая область относится к молекулярной степени дисперсности, размер частиц менее 10^-9 м. В нулевой области системы гомогенные, поэтому там не может быть никакой удельной поверхности. Чем меньше размер частиц, как видно из го., тем больше удельная поверхность сильнее развит поверхностный слой и сильнее выражено поверхностное явление.
Sуд =
 = 12*10^6 м^-1
= 12*10^6 м^-1
Sуд = Sсум/mсум (м2/кг)
Выразим суммарную массу всех частиц дисперсной фазы на основании величины плотности этих частиц
 m сум. = V*
m сум. = V*
 =4/3
=4/3
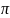 r^3*
(3)
r^3*
(3)
Подставим в выражение (3) формулу (2):
Sуд =
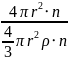 =
=
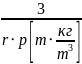 = м2/кг
= м2/кг
Sуд =
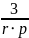 =
=
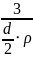 =
=
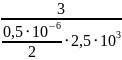 =
=
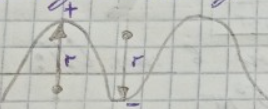
Кривизна п. (Н) – отклонение поверхности от плоскости
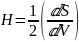
Если частицы имеют сферическую форму,
то кривизна поверхности Н будет
равна
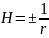 , где r – радиус кривизны
поверхности, а если цилиндрическую:
, где r – радиус кривизны
поверхности, а если цилиндрическую:
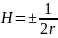
Кривизна поверхности цилиндрической формы в 2 раза меньше сферической
Броуновское движение частиц характеризуется величиной среднего квадратичного сдвига.
Средний квадратичный
сдвиг обозначается
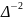 или
или
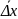
=
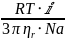 = постоянная Больцмана
= постоянная Больцмана
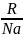 = k = 1,38*10^-3 Дж/К =
= k = 1,38*10^-3 Дж/К =
 (м)
(м)
Диффузия D =
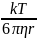 (м2/с)
(м2/с)
= 2Di
Задача №3
Определите частичную концентрацию золя Al2O3 исходя из следующих данных: массовая концентрация 0,3 г/л, коэффициент диффузии сферических частиц золя 2∙10-6 м 2 /сут, плотность Al2O3 4 г/см 3 , вязкость среды 1∙10-3 Па∙c, температура 293 К.
Дано: T = 293 K С = 0,3 г/л D (Al2O3) = 2∙10-6 м 2 /сут Al2O3 = 4 г/см 3
|
Решение: Численная конц-я равна отношению массовой концентрации (кг/м3) к массе всех частиц (кг)
Переводим данные в сист. СИ: C=0,3 Г/Л = 0,3 10^-3 кг/ 10^-3 м^3 D = 2*10^-6/24*60*60 = 2,3 *10^-11 м/с = 4,0*10^-3 кг/ 10^-6 м3 = 4,0 *10^3 кг/м2 |
Найти –
|
|
m частиц = V*
=
4/3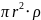 ,
кг
,
кг
Размер частиц определяем, используя величину коэффициента диффузии.
D =
 r =
r =
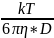 = 1,38*10^-3*293/6*3,14*1*10^-3*2,3*10^-11 = 9,3*10^-9 м
= 1,38*10^-3*293/6*3,14*1*10^-3*2,3*10^-11 = 9,3*10^-9 м
m=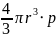 = 4/3*3,14*(9,3*10^-9)^3*4*10^3 = 1,3*10^-21 кг
= 4/3*3,14*(9,3*10^-9)^3*4*10^3 = 1,3*10^-21 кг

Поверхностное натяжение – избыточная энергия, приходящаяся на единицу площади поверхности:
 (Дж/м2=Н/м)
(Дж/м2=Н/м)
Физическая природа поверхностного натяжения характеризует различия в нескомпенсированности поля межмолекулярных сил на межфазных поверхностях. Поверхностное натяжение характеризует различия в интенсивности межмолекулярных взаимодействий, граничащих фаз. Чем сильнее межмолекулярные связи в веществе, тем больше поверхностное натяжение на его межфазной поверхности.
С т/д – ской точки зрения:
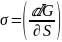 Р – давление, Т – температура, n
– число молей компонентов
Р – давление, Т – температура, n
– число молей компонентов
Взаимосвязь поверхностного натяжения, тепер. и полной поверхностной энергии (внутренней энергии поверхностного слоя) Us выраж.уравнением Гиббса – Гельмгольца.
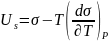
где
 – температура коэф.поверхностного
натяжения, (Дж/м2*кг)
– температура коэф.поверхностного
натяжения, (Дж/м2*кг)
Энтропия поверхностного слоя в соответствии со 2-м з.т/д-ки
Ss= Ss = -
Ss = -
Теплота образования единицы поверхности
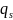 – количество теплоты, которое необходимо
сообщить телу, чтобы при T=const
увеличить его поверхность на единицу
площади.
– количество теплоты, которое необходимо
сообщить телу, чтобы при T=const
увеличить его поверхность на единицу
площади.
Силовой (механический) подход к объяснению поверхностного натяжения |
Энергетический (термодинамический) подход к объяснению поверхностного натяжения |
Основываясь на законах механики
величину
Отсюда: = F/L (Дж/м2) = (Н/м), где F – сила, приложенная к единице длины контура (L) поверхности раздела фаз. |
Для увеличения поверхности необходимо вывести молекулы из объёма на поверхность S. При этом надо совершить работу против внутреннего давления для образования единицы площади новой поверхности раздела фаз. И мерой этой работы является поверхностное натяжение. С точки зрения термодинамики поверхностное натяжение также равно избыточной удельной свободной поверхностной энергии Гельмгольца или Гиббса единицы площади поверхности при определённой температуре: A
=
* S
= A или = G (Дж/м2 = Н/м1) Полезная работа в обратимом процессе максимальна и равна изменению энергий Гиббса или Гельмгольца, взятых с обратным законом. В этом случае величина будет равна:
=
Следовательно, в общем случае – это частная производная любого термодинамического потенциала по площади межфазной поверхности. |

 среды = 1∙10-3 Па∙c
среды = 1∙10-3 Па∙c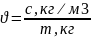
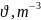 - ?
- ?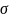 рассматривают как силу, действующую
тангенциально на единицу длины контура,
ограничивающего поверхность, и
стремящуюся сократить поверхность
до минимума при данном отношении
объёмов фаз. Величина
– мера стремления поверхности к
сокращению, вследствие действия
межмолекулярных сил.
рассматривают как силу, действующую
тангенциально на единицу длины контура,
ограничивающего поверхность, и
стремящуюся сократить поверхность
до минимума при данном отношении
объёмов фаз. Величина
– мера стремления поверхности к
сокращению, вследствие действия
межмолекулярных сил. = A/S, при S = 1 м2
= A/S, при S = 1 м2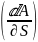 =
=
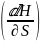 =
=