
optica-metod / Lab05
.pdfФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ АКАДЕМИКА М.Ф. РЕШЕТНЕВА
Кафедра физики
Баранов А.Г., Чернышова Л.И.
Изучение спектра атома водорода и определение постоянной Ридберга
Методическая разработка к лабораторной работе №5
Красноярск
2005
ВВЕДЕНИЕ
Спектр излучения представляет собой важную характеристику вещества, которая позволяет установить его состав, особенности его строения, свойства атомов и молекул.
Атомы газов испускают линейчатые спектры, состоящие из групп спектральных линий, называемых спектральными сериями. Положение линий в атомных спектрах может быть объяснено только на основе квантовой механики. Энергия электронов в атоме может принимать не любые, а вполне определенные значения, образующие дискретный набор. Состояния с различивши значениями энергии называются уровнями. Спектральные линии излучения возникают при переходе электронов с одного уровня (Еm) на другой, более низкий (Ek). При этом испускается квант света, энергия которого равна разности энергий этих двух уровней:
hvmk = Em - Ek . Здесь h - постоянная Планка, равная 6,625×10-34 Дж-с; v - частота излучения.
Наиболее простой спектр имеет атом водорода. Длины волн его спек- тральных линий определяются по формуле Бальмера-Ридберга
1 |
|
1 |
|
1 |
|
|
= R |
|
− |
|
, |
λ |
|
m2 |
|||
k 2 |
|
|
|||
где λ - длина волны света, испускаемого атомом (длина волны спек- тральной линии), R - постоянная Ридберга, k - номер энергетического уровня атома, на который совершается переход, m - номер уровня, с которого переходит электрон при излучении электромагнитной волны. Каждой серии атома водорода соответствует свое определенное значение k. Значение m представляет собой последовательный ряд чисел от (k + 1) до ¥.
Спектр атома водорода можно представить в виде нескольких серий.
Серия Лаймана (ультрафиолетовая часть спектра)
1 |
|
1 |
|
1 |
|
|
||
|
= R |
|
|
− |
|
|
|
, m=2,3,4,… k=1 |
λ |
2 |
m |
2 |
|||||
|
1 |
|
|
|
|
|||
Серия Бальмера (видимая часть спектра)
1 |
|
1 |
|
1 |
|
|
|
|
|
= R |
|
− |
|
|
, m=3,4,5,… |
k=2 |
|
λ |
22 |
m2 |
||||||
|
|
|
Серия Пашена (инфракрасная часть спектра)
1 |
|
1 |
|
1 |
|
|
|
|
|
= R |
|
− |
|
|
, m=4,5,6,… |
k=3 |
|
λ |
32 |
m2 |
||||||
|
|
|
В данной лабораторной работе изучается серия Бальмера (k = 2)
2
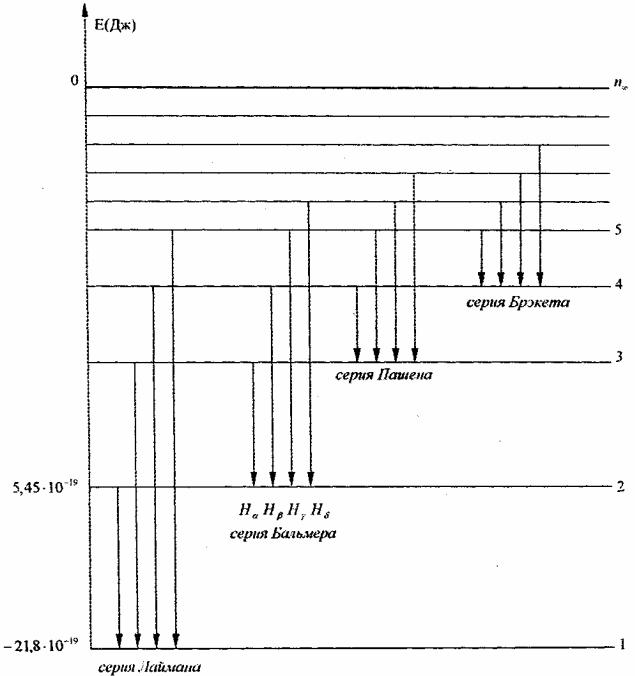
Рис. 1
На рисунке схематично представлено образование серии водородного спектра. Горизонтальными линиями графически представлены уровни энергии атома водорода. Вертикальные линии показывают переходы с одного уровня на другой.
3
ЦЕЛЬ ЛАБОРАТОРНОЙ РАБОТЫ
Цель данной лабораторной работы:
а) Измерение длин волн трех линий в спектре атома водорода, которые представляют собой три первые линии серии Бальмера. Эти линии имеют следующие обозначения:
Нα |
- красная линия (m = 3); |
Hβ |
- зелено-голубая линия (m = 4); |
Нγ |
- сине-фиолетовая линия (m = 5); |
б) Вычисление значения постоянной Ридберга с помощью каждого найденного значения длины волны и соответствующего ему значения числа т. Критерием справедливости сериальной закономерности будет служить постоянство значения R, найденного независимо во всех четырех случаях.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Врезультате углубления представлений о природе света выяснилось, что в оптических явлениях обнаруживается своеобразный дуализм. Наряду с такими свойствами света, которые самым непосредственным образом свидетельствуют о его волновой природе (интерференция, дифракция), имеются и другие свойства, столь же непосредственно обнаруживающие его корпускулярную природу (фотоэффект, явление Комптона).
В1924 г. Луи де-Бройль выдвинул гипотезу, что дуализм не является особенностью одних только оптических явлений, но имеет универсальное значение. Допуская, что частицы вещества наряду с корпускулярными свойствами имеют также и волновые, де-Бройль перенес на случай частиц вещества те же правила перехода от одной картины к другой, какие спра- ведливы в случае света.
В развитие идеи де-Бройля о волновых свойствах вещества Э. Шрёдингер получил в 1926 г. уравнение. Шрёдингер сопоставил движению микрочастицы комплексную функцию координат и временя, которую он назвал волновой функцией и обозначил буквой «пси» (y или Y). В настоящее время ее принято называть пси-функцией.
Пси-функция характеризует состояние микрочастицы. Вид функции получается из решения уравнения Шрёдингера, которое выглядит следую- щим образом:
- |
h2 |
Ñ2Y + UY = ih |
¶Y , |
(1) |
|
2m |
|||||
|
|
¶t |
|
где m – масса частицы, U - функция координат и времени, равная взятому с обратным знаком потенциалу силового поля, в котором движется частица (U = -П (х, у, z, t)), i - мнимая единица, Ñ2 - оператор Лапласа; результат действия оператора Лапласа на некоторую функцию представляет собой
4
сумму вторых частных производных этой функции по координатам, в нашем случае:
Ñ2 Y = |
¶2 Y |
+ |
¶2 Y |
+ |
¶2 Y |
, |
(2) |
|
¶x2 |
|
¶y 2 |
|
¶z 2 |
|
|
Из уравнения (1) следует, что вид пси-функции определяется функцией U, т.е. в конечном счете характером сил, действующих на частицу.
Уравнение Шрёдингера является основным уравнением нерелятивист- ской квантовой механики. Оно не может быть выведено из других соот- ношений. Его следует рассматривать как исходное основное предположение, справедливость которого доказывается тем, что все вытекающие из него следствия самым точным образом согласуются с опытными фактами.
Шрёдингер установил свое уравнение, исходя из оптико- механической аналогии. Эта аналогия заключается в сходстве уравнений, описывающих ход световых лучей, с уравнениями, определяющими траектории частиц в аналитической механике. В оптике ход лучей удовлетворяет принципу Ферма, а в механике вид траектории удовлетворяет так называемому принципу наименьшего действия.
Если силовое поле, в котором движется частица, стационарно, то по- тенциал не зависит явно от времени и функция U имеет смысл потенци- альной энергии. В этом случае решение уравнения Шрёдингера распадается на два множителя, один из которых зависит только от координат, другой - только от времени:
|
E |
|
|
|
-i× |
|
×t |
|
|
|
|
|||
Ψ(x, y, z, t) = ψ (x, y, z)e |
h |
, |
(3) |
|
Здесь Е - полная энергия частицы, которая в случае стационарного поля остается постоянной. Чтобы убедиться в справедливости выражения (3), подставим его в уравнение (1). В результате получим соотношение:
|
|
h2 |
|
|
E |
|
E |
|
E |
|
E |
|||||||||
|
|
|
-i× |
|
×t |
|
-i× |
|
×t |
|
-i× |
|
|
×t |
||||||
|
|
h |
|
h |
|
h |
||||||||||||||
- |
|
|
|
× e |
|
|
× Ñ2ψ + U ×ψ × e |
|
= ih - i |
|
×ψ × e |
|
|
|||||||
2m |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-i× |
|
×t |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Сократив обе части уравнения на множитель e |
h , придем к |
|||||||||||||||||||
дифференциальному уравнению, определяющему функцию ψ : |
||||||||||||||||||||
Ñ2ψ + |
2m |
(E -U )ψ = 0 . |
|
|
|
|
|
|
(4) |
|||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение (4) называется уравнением Шрёдингера для стационарных |
||||||||||||||||||||
состояний. Это уравнение часто пишут в виде: |
|
|
|
|
|
|
|
|||||||||||||
- |
h2 |
|
Ñ2ψ + Uψ = Eψ . |
|
|
|
|
|
|
(5) |
||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правильную интерпретацию пси-функции дал М. Борн в 1926 году. Согласно Борну квадрат модуля пси-функции определяет вероятность dP то- го, что частица будет обнаружена в пределах объема dV:
dP = A × |
|
Y |
|
2 × dV = A × Y* × Y × dV , |
(6) |
|
|
5
где А - коэффициент пропорциональности.
Интеграл от выражения (6), взятый по всему объему, должен равняться единице:
∫dP = A∫Y × Y × dV = 1 |
(7) |
Действительно, этот интеграл дает вероятность того, что частица находится в одной из точек пространства, т.е. вероятность достоверного события, которая равна единице.
В квантовой механике принимается, что пси-функция допускает умно- жение на отличное от нуля произвольное комплексное число С, причем Y и СY описывают одно и то же состояние частицы. Это обстоятельство по- зволяет выбрать пси-функцию так, чтобы она удовлетворяла условию:
∫Y* × Y × dV = 1 |
(8) |
Условие (8) носит название условия нормировки. Функции, удовлетворяющие этому условию, называются нормированными. Для нормированной пси-функция выражение (6) имеет вид:
dP = |
|
Y |
|
2 dV = Y × Y × dV = 1 |
(9) |
|
|
(это вытекает из сравнения формул (7) и (8) ). Из (9) заключаем, что квадрат модуля пси-функции дает плотность вероятности, отнесенную к единице объема, нахождения частицы в соответствующем месте пространства.
В случае стационарного силового поля пси-функция имеет вид
|
E |
|
|
E |
|
|
||
-i× |
|
×t |
Y* × e |
-i× |
|
×t |
× Y |
|
|
|
|
||||||
Y* × Y = e |
h |
|
h |
(10) |
||||
так что плотность вероятности равна Y × Y и, следовательно, от времени не зависит. По этой причине состояния, описываемые пси-функциями вида (3), и были названы стационарными.
Из смысла пси-функции вытекает, что квантовая механика имеет статистический характер. Она не позволяет определить местонахождение частицы в пространстве или траекторию, по которой движется частица. С помощью пси-функции можно лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства. На первый взгляд может показаться, что квантовая механика дает значительно менее точное и исчерпывающее описание движения частиц, чем клас- сическая механика, которая определяет «точно» местоположение и скорость частицы в каждый момент времени. Однако в действительности это не так. Квантовая механика гораздо глубже вскрывает истинное поведение микрочастиц. Она лишь не определяет того, чего нет на самом деле. В применении к микрочастицам понятия определенного местоположения и траектории, как мы уже отмечали, вообще теряют смысл.
Уравнение Шрёдингера позволяет найти пси-функцию данного состояния и, следовательно, определить вероятность нахождения частицы в различных точках пространства. Однако этим далеко не исчерпывается зна- чение указанного уравнения.
6

Всоответствии со своим смыслом пси-функция должна быть однозначной, непрерывной и конечной (за исключением, быть может, особых точек). Кроме того, она должна иметь непрерывную и конечную производ- ную. Совокупность перечисленных требований носит название стандартных условий.
Вуравнение Шрёдингера входит в качестве параметра полная энергия частицы Е. В теории дифференциальных уравнений доказывается, что уравнения вида (5) имеют решения, удовлетворяющие стандартным усло- виям, не при любых значениях параметра (т.е. энергии Е). а лишь при не- которых избранных значениях. Эти значения называются собственными значениями соответствующей величины (в нашем случае энергии). Решения, соответствующие собственным значениям Е называются собственными функциями задачи.
Совокупность собственных значений называется спектром величины. Если эта совокупность образует дискретную последовательность, спектр называется дискретным. Если собственные значения образуют непрерывную последовательность, спектр называют непрерывным или сплошным. В дальнейшем мы ограничимся рассмотрением только таких задач, у которых спектр собственных значений является дискретным.
Вслучае дискретного спектра собственные значения и собственные функции можно пронумеровать:
E1 , E 2 ,..., E n ,...; (11) Ψ1 , Ψ2 ,..., Ψn ,... .
Таким образом, квантование энергии получается из основных положений квантовой механики без каких-либо дополнительных предположений.
Нахождение собственных значений и собственных функций, как правило, представляет весьма трудную математическую задачу. Обратимся к системе, состоящей из неподвижного ядра с зарядом Ze, (Z - целое число) и движущегося вокруг него электрона. При Z > 1 такая система называется водородоподобным ионом; при Z = 1 она представляет собой атом водорода.
Потенциальная энергия электрона равна: U = − Ze2 . r
Рассмотрим атом водорода: Z = 1; U = - e2 , где r - расстояние r
электрона от ядра. Следовательно, уравнение Шрёдингера имеет вид:
2 |
|
|
|
e |
2 |
|
2me |
|
|
||||
Ñ ψ + |
|
|
E + |
|
|
ψ = 0 |
h |
2 |
r |
||||
|
|
|
|
|||
где me - масса электрона.
Поле, в котором движется электрон,
ным.
(12)
является центрально симметрич-
7
Уравнение (1.2) имеет требуемые (т.е. однозначные, конечные и непрерывные) решения в следующих случаях: 1) при любых положительных значениях E; 2) при дискретных отрицательных значениях энергии, равных:
En = − |
m e4 |
,(n = 1,2,3,...) |
|
|
e |
(13) |
|||
2h2 n2 |
||||
|
|
|
где n - главное квантовое число.
Случай Е > 0 соответствует электрону, пролетающему вблизи ядра и удаляющемуся снова на бесконечность. Случай E < 0 соответствует электрону, связанному с ядром. При этом, как видно из решения уравнения (12), представленного формулой (13), электрон в атоме может иметь не любые значения энергии, а вполне определенные.
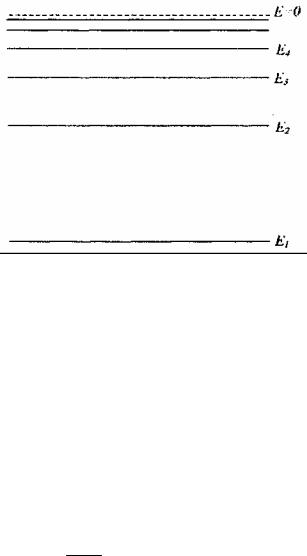
Схематическое изображение энергетических уровней электрона в атоме водорода представлено на рис. 2.
Рис. 2. Схема энергетических уровней электрона в атоме водорода
При переходе атома из состояния с n = m в состояние n = k излучается фотон, энергия которого определяется:
hω = Em − Ek |
= − |
me e4 |
|
1 |
− |
1 |
|
|
|
|
|
|
, |
(14) |
|||
2h2 |
|
m2 |
||||||
|
|
k 2 |
|
|
|
|||
где ω - циклическая (круговая) частота световой волны. Таким образом, частота испущенного света равна:
ω = |
m e4 |
|
1 |
− |
1 |
|
|
|
|||
e |
|
|
|
|
|
|
|
, |
(15) |
||
2h |
3 |
|
2 |
m |
2 |
||||||
|
|
k |
|
|
|
|
|
|
|||
где |
k |
и |
m |
|
- |
соответствующие значения главного |
квантового числа n. |
||||
4
Постоянную величину R'= me e3 называют постоянной Ридберга. Исходя из
2h
этого, частота испущенного атомом водорода фотона при переходе электрона из состояния с главным квантовым числом m в состояние с главным квантовым числом k запишется так:
8

|
1 |
|
1 |
|
|
|
ω = R' |
|
− |
|
|
, |
(16) |
|
m2 |
|||||
k 2 |
|
|
||||
Изучение атомных спектров послужило ключом к познанию строения атомов. Прежде всего было замечено, что линии в спектрах атомов распо- ложены не беспорядочно, а объединяются в группы или, как их называют, серии линий. Отчетливее всего это наблюдается в спектре атома водорода, для которого, как отмечается во введении, наблюдаются следующие серии линий: Лаймана, Бальмера, Пашена, Пфунда, Брекета. Как видно из формул, описывающих отдельные серии спектральных линий, представленных на стр. 3, эти формулы легко могут быть сведены к одной вида (16), где при заданном k число m принимает все целые значения, начиная от (k+1). Выражение (16) называют обобщенной формулой Бальмера.
В спектроскопии принято характеризовать спектральные линии не частотой, а обратной длине волны величиной [l]:
v'= |
1 |
= |
ω |
|
|
|
|
. |
(17) |
||
λ |
2πc |
||||
Отсюда и постоянная Ридберга будет иметь вид:
R = |
m e4 |
|
= |
m e4 |
|
||
e |
|
e |
|
. |
(18) |
||
2πc2h |
3 |
4ch |
3 |
||||
|
|
|
|
|
|
||
1
В СИ (учитывая постоянную 4πε0 в представлении потенциальной
энергии электрона в атоме водорода в формуле (12)) постоянная Ридберга имеет вид:
R = |
m e4 |
|
= |
|
m e4 |
|
|
||||
|
e |
|
|
|
e |
|
|
|
(19) |
||
8cε |
2 |
2h |
3 |
16cε |
2 |
h |
3 |
||||
|
0 |
|
|
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
R = 1,1 × 107 м-1
Окончательно, для определения длины волны излученного фотона получаем соотношение:
1 |
|
1 |
|
1 |
|
|
|
= R |
|
+ |
|
|
(20) |
λ |
|
m 2 |
||||
k 2 |
|
|
||||
ОПИСАНИЕ И ПРИНЦИП ДЕЙСТВИЯ ЛАБОРАТОРНОЙ УСТАНОВКИ
Приборы и принадлежности: газоразрядная водородная трубка, монохроматор, источник напряжения, ртутная лампа.
Изучение спектра атома водорода осуществляется с помощью установки, состоящей из прибора для спектральных исследований - монохроматора УМ-2, источника излучения - водородной газоразрядной трубки и источника высокого напряжения.
9
При замыкании ключа на источнике высокого напряжения в трубке появляется электрический разряд, сопровождающийся излучением.
В настоящей работе с помощью монохроматора исследуются спектральные линии серии Бальмера (k = 2; m = 3,4,5,6 …). Наиболее интенсивными линиями в этой серии являются:
красная, Нα, (m = 3), зелено-голубая, Нβ, (m = 4), фиолетово-синяя, Нγ, (m = 5).
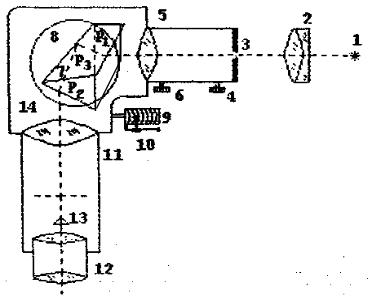
Оптическая схема монохроматора представлена на рис. 3.
Рис. 3. Оптическая схема монохроматора
Свет от источника излучения (1) концентрируется с помощью конденсора (2) на входной щели (3), ширина которой (0,02-0,03) мм регулируется микрометрическим винтом (4). Конденсор в простейшем случае представляет собой плосковыпуклую линзу, служащую для концентрации светового потока в узкий параллельный пучок. Источник излучения и конденсор могут перемещаться вдоль оптической скамьи и закрепляться на ней винтами. Свет через входную щель монохроматора попадает на коллиматорный объектив (5), снабженный микрометрическим винтом (6). (Коллиматором называется входная труба монохроматора). Винт позволяет смещать объектив относительно щели при фокусировке спектральных линий различных цветов. Затем свет параллельным пучком падает на диспергирующую призму (7), которая является одним из основных элементов монохроматора. Назначение диспергирующей призмы заключается в пространственном разделении спектральных линий различных длин волн. Это разделение основано на явлении дисперсии света.
10
