TsOS_Ekzamen_2021_1
.pdf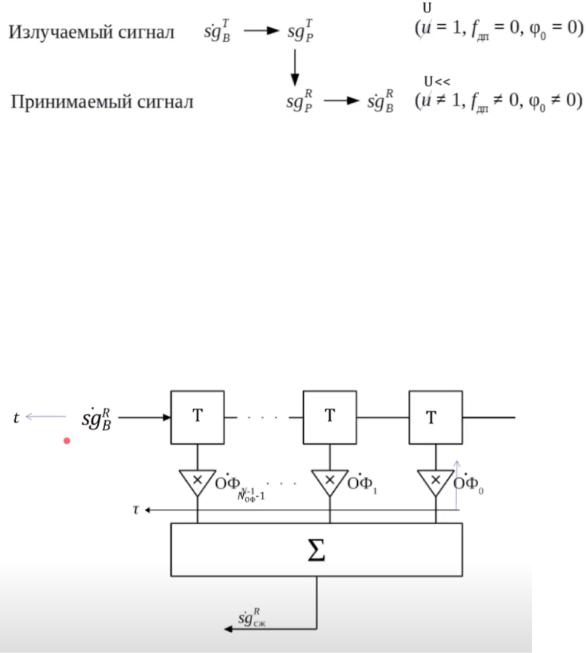
19. Фильтрация (сжатие) сложных сигналов. Комплексный согласованный фильтр. Реализация во временной области.
Сигнал проходит следующие этапы:
1)Синтез исходного сигнала
2)Поднятие сигнала несущую частоту (на гигагерцовые частоты)
3)Передача сигнала
4)Снятие сигнала с несущей частоты (с гигагерцовых частот)
Т.к. фильтр делаем согласованный, то нужна опорная функция.
В качестве опорной функции возьмем изначальный сигнал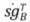 
и подвергнем его
процедуре комплексной сопряженности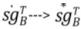 
. То есть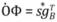 
ОФ - опорная функция
М-последовательности не используем, т.к. там только действительная часть числа, а у нас комплексные числа.
Функциональная схема комплексного согласованного фильтра:
Здесь сигнал и опорная функция направлены в одну сторону, но эта сторона обратная от привычной.
Все здесь комплексное - если с триггерами проблем не возникает, то умножители надо модифицировать.
Функциональная схема комплексного умножителя:
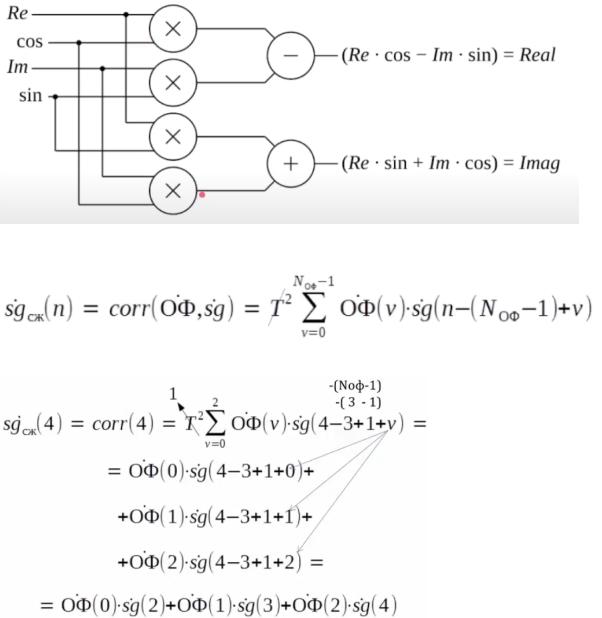
Согласованная фильтрация во временной области называется асинхронной корреляцией и имеет вид:
Пример корреляции (для одной точки):
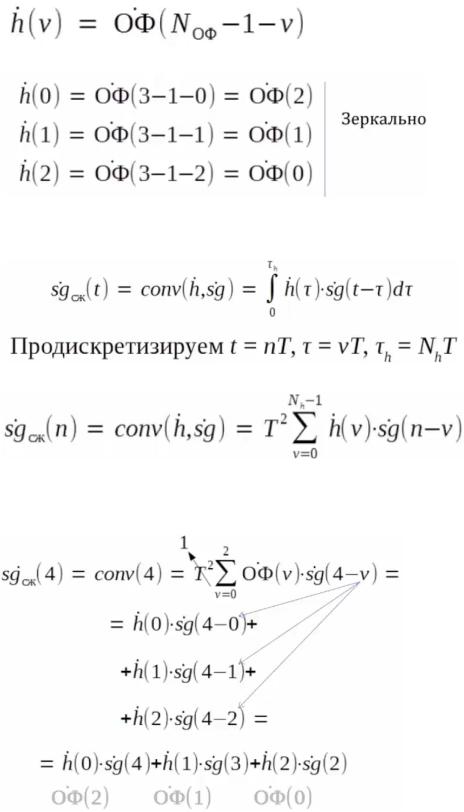
20. Реализация согласованного фильтра в частотной области. Сравнение решения задачи сжатия во временной и частотной области.
Реализация согласованного фильтра в частотной области.
Для реализации согласованного фильтра в частотной области воспользуемся импульсной характеристикой.
Импульсная характеристика - это опорная функция, вывернутая наизнанку относительно середины.
Пример при Nоф = 3:
Сигнал и опорная функция направлены в разные стороны для реализации Свертки
(Convolution).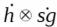 
:
Тогда конечная формула:
Далее пример для сравнения использования Опорной функции (ОФ) и Импульсной
Характеристики (h):
Оказывается свертка - это обратное преобразование Фурье от произведения преобразований Фурье множителей:
Тогда сжатие сигнала имеет следующий вид:
ifft - обратное преобразование Фурье, fft - преобразование Фурье.
Сравнение решения задачи сжатия во временной и частотной области.
Сжатие сигнала во временной области и в частотной области дает одинаковый результат, но сжатие в частотной области сильно экономит вычислительные мощности.
Пример сжатия сигнала:
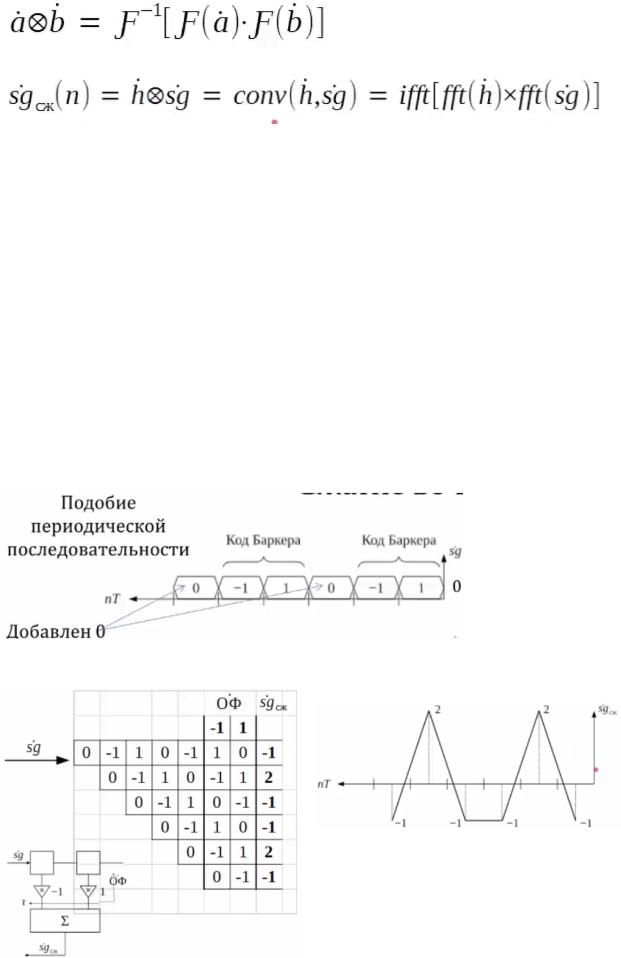
Возьмем код Баркера 01, тогда:
Опорная Функция: ОФ = 1, -1 Импульсная характ.: h = -1, 1
Сжатие во временной области
Создадим период. последовательность кода и немного расширим сигнал, добавив
нули:
Получившуюся последовательность заносим в согласованный фильтр:
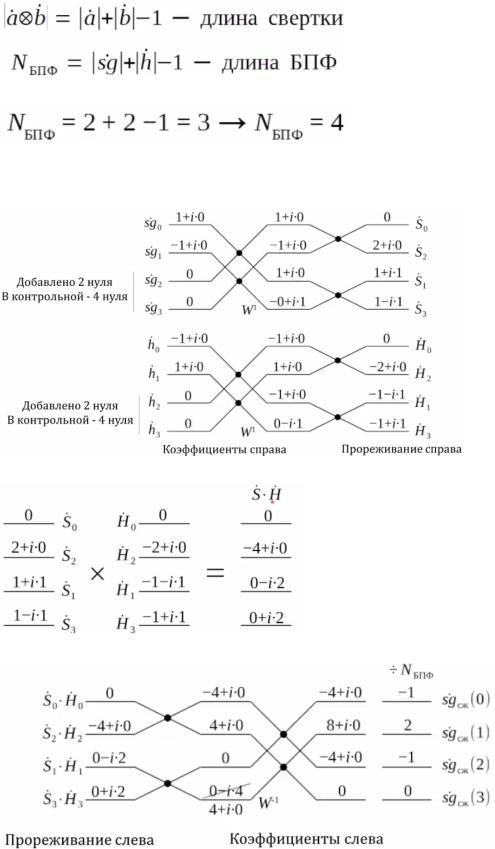
Сжатие в частотной области
Первое что нужно сделать, это выбрать длину свертки(длина периода). Для того, чтобы сжатие прошло успешно, необходима длина свертки, равная:
Соответственно, для решаемой выше задачи(добавляем до полной степени двойки):
Теперь вычисляем БПФ. Сначала для сигнала, потом для импульсной характеристики
(следуем формуле корреляции):
Далее перемножаем векторы:
И последним шагом производим ОБПФ:
21. Определение формы сжатого ЛЧМ-pass сигнала. Определение формы сжатого ЛЧМ-base сигнала.
Определение формы сжатого ЛЧМ-pass сигнала.
Очень много картинок, рисуйте быстрее. По сути 4 раза одно и тоже делал, есть что сократить.
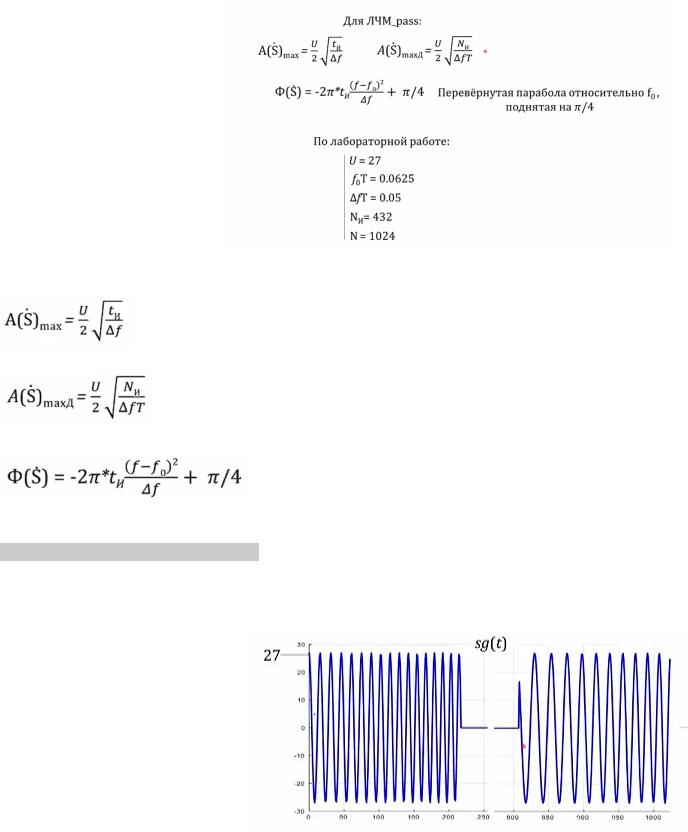
Возьмем сигнал со следующими характеристиками:
-Амплитуда U
-Цифровая 0
-Цифровая полоса ∆
-Длительность импульса И
-Длина периода (длина
БПФ) N Для ЛЧМ-pass есть
следующие формулы (по Гоноровскому И.С): Максимальное значение амплитуды:
Или после перехода к относительным единицам (и к цифровым):
Формула для фазы:
Гоноровский доказал, что фазовая характеристика имеет квадратичный вид и поднята на π/4.
После вычислений с помощью matlab
а) Расположение сигнала и импульсной характеристики от центра: − и/2 ... + и/2
Получаем:
sg(t): левая половина сигнала из-за
периодичности, перенесена
направо. Частота изменения сигнала растет слева направо. Такой сигнал считается
неестественным. Для удобства изображения из середины была убрана половина значений сигнала.
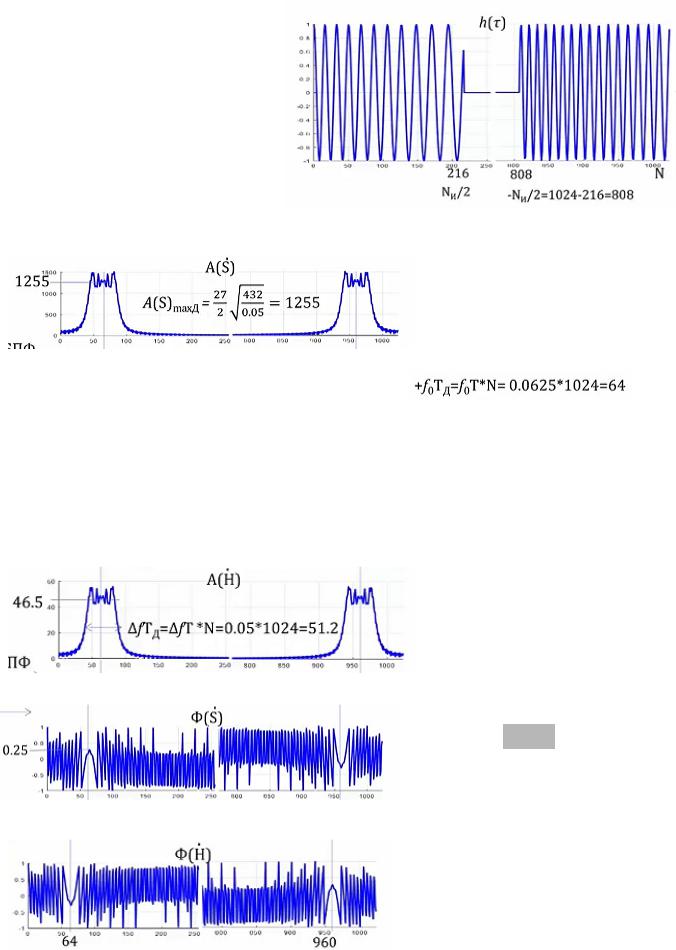
Длина БПФ - 1024.
Импульсная характеристика. Зеркальная копия sg(t). Поскольку длина сигнала 432, то
половина сигнала расположится от 0 до
216. Вторая его часть, от 1024-216=808 до 1024.
Вычисляем БПФ от сигнала и импульсной характеристики. Амплитудный спектр:
Спектр расположится относительно 0 и − 0. У нас есть
значение 0Т. Тогда дискретная 0 --------- |
> |
И видим пики на 64 и 1024-64 = 960.
Максимальное значение амплитудного спектра вычисляется по формуле Гоноровского(на фото выше внутри спектра).
В относительных величинах:
Полоса сигнала(по формуле внутри, снизу) - разность на концах стрелки внутри
спектра. А максимальное значение амплитуды фазовой характеристики в 27 раз
меньше. Так как в формуле Гоноровского в числителе стоит 1. 
Фазовые характеристики:
Видим параболы на 0(вниз)
и − 0(вверх). Матлаб
изображает фазу от − π до π. Поэтому переносит параболу
в эти границы. То есть эта
осцилляция - перенос веток
параболы. Начало параболы
в π/4согласно Гоноровскому.
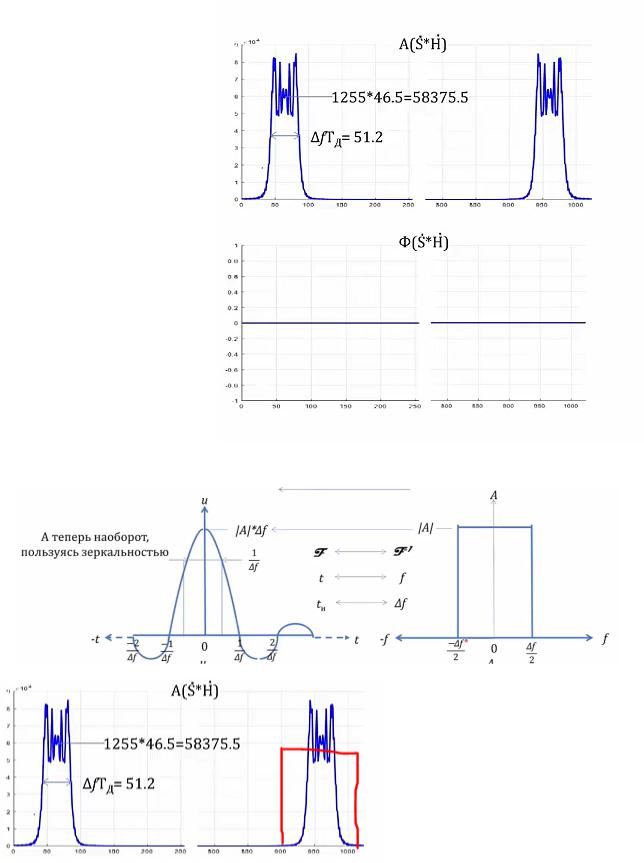
Вторая картинка - фаза импульсной характеристики. Сейчас мы имеем спектр сигнала и спектр опорной функции. Перемножаем амплитуды и складываем фазы. Фаза обнулилась, так как они зеркальные относительно горизонтальной оси.
Воспользуемся симметрией преобразования Фурье и обратного преобразования Фурье.
Представим нашу картинку как
прямоугольник с уровнем
58375.5, шириной 51.2.
Проводим обратное
преобразование от этого
прямоугольника.
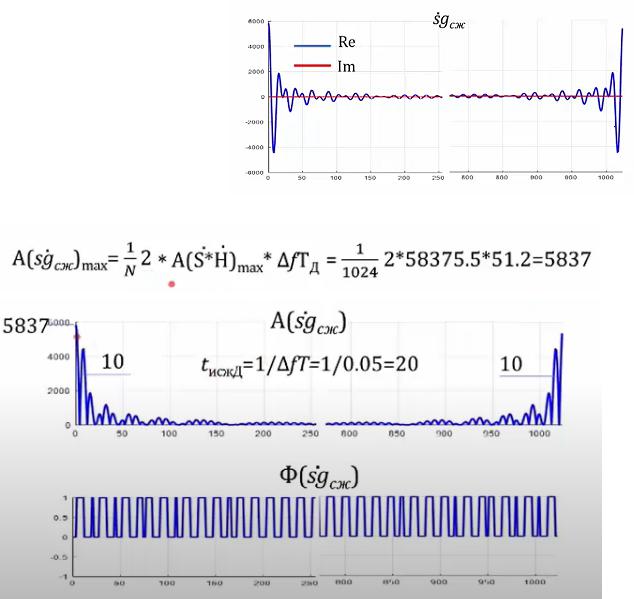
Получаем такой сигнал. Реальная часть - sinc распавшийся на 2 части. Мнимая часть - 0.
Ниже вычисляем амплитуду и ширину сжатого сигнала = 20, по 10 на две половины. Фаза следует за переходами сигнала в ноль
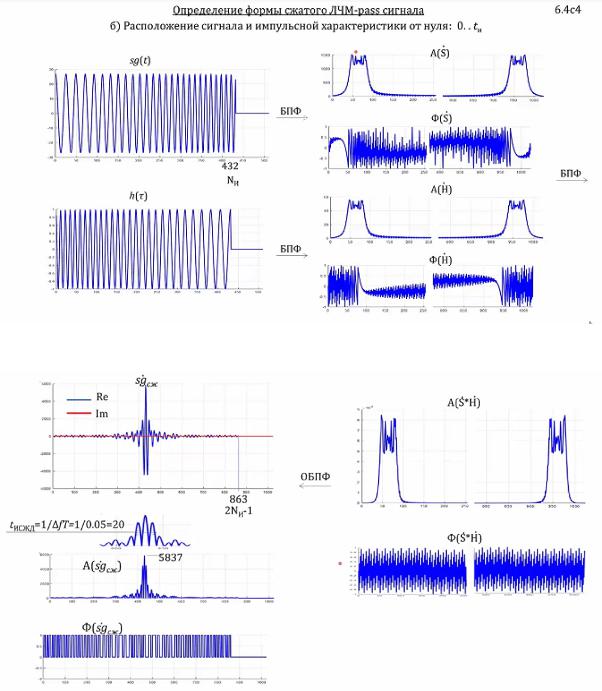
б) Расположение сигнала и импульсной характеристики от центра: 0 ... и
рис.1 снизу) Изменилось расположение сигнала. на амплитуду оно никак не влияет
значения те же, только на фазу.
Парабола остается, только ее левая ветвь становится почти горизонтальной, правая
стала больше осциллировать. Фаза импульсной характеристики на нее совсем не
похожа.
рис.2 снизу) Проводим аналогичные операции. Перемножаясь, фазы не дадут 0, что
при обратном преобразовании Фурье сжатый сигнал сдвигается относительно нуля. Середина смещается на и, вся свертка - 2и − 1. Длительность пика остается равной
20. Сам сигнал получается более сжатым.
